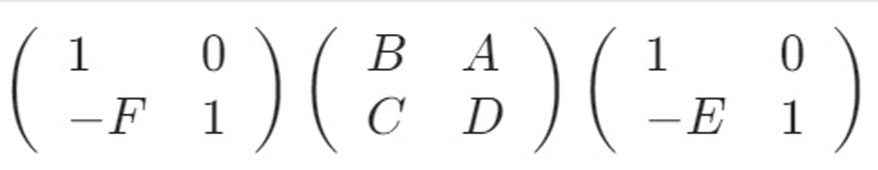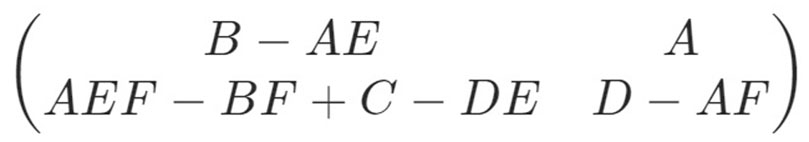
近軸光線の屈折について、基礎からご説明します。
近軸とは、光軸に極限まで近付いた光線のことで、理想的な結像をすることは経験的にも分かっていますが、そのままでは作図も考察も出来ないため、常に高さ(h)のある光線を想定することになります。
言い換えますと、近軸光線追跡は、完全無収差の光学系による理想結像をシミュレートするものです。
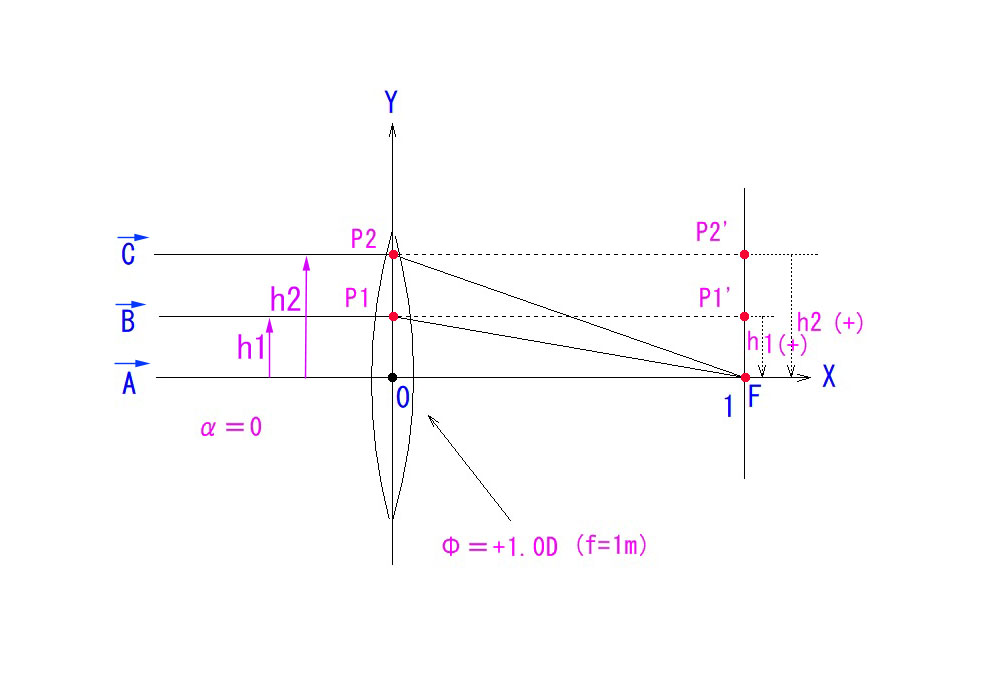
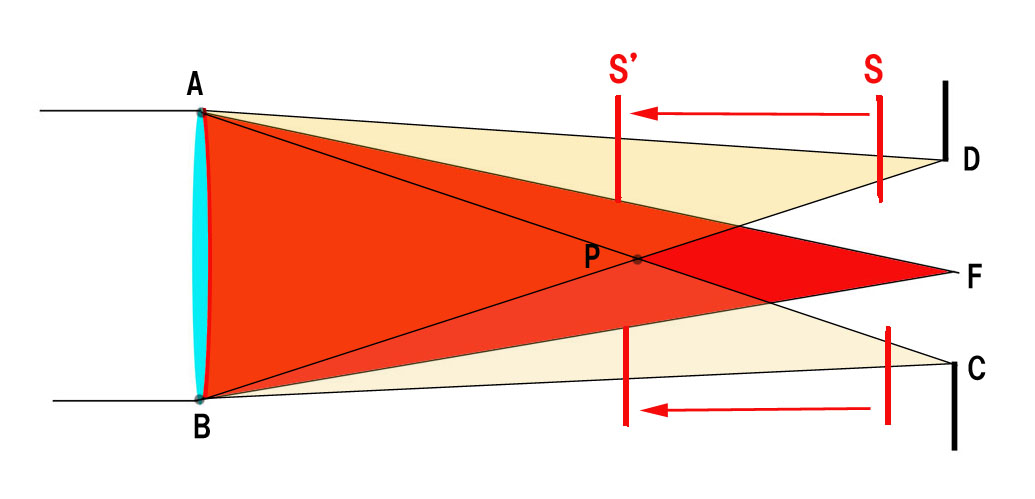
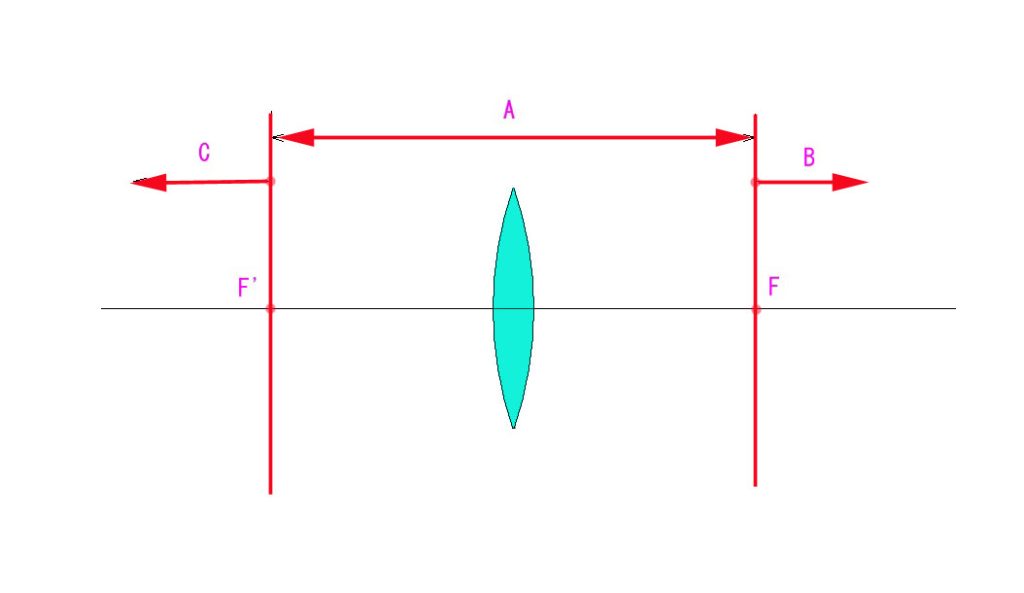
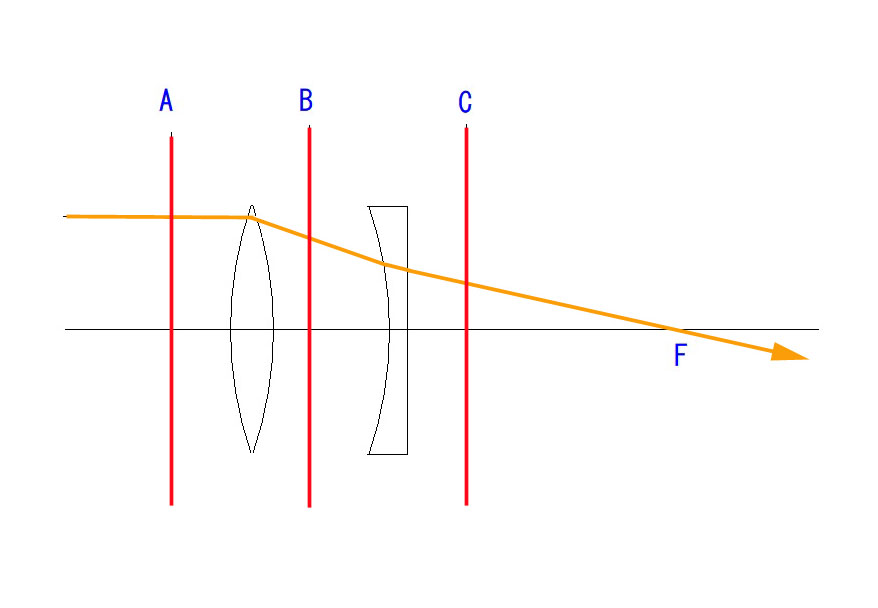
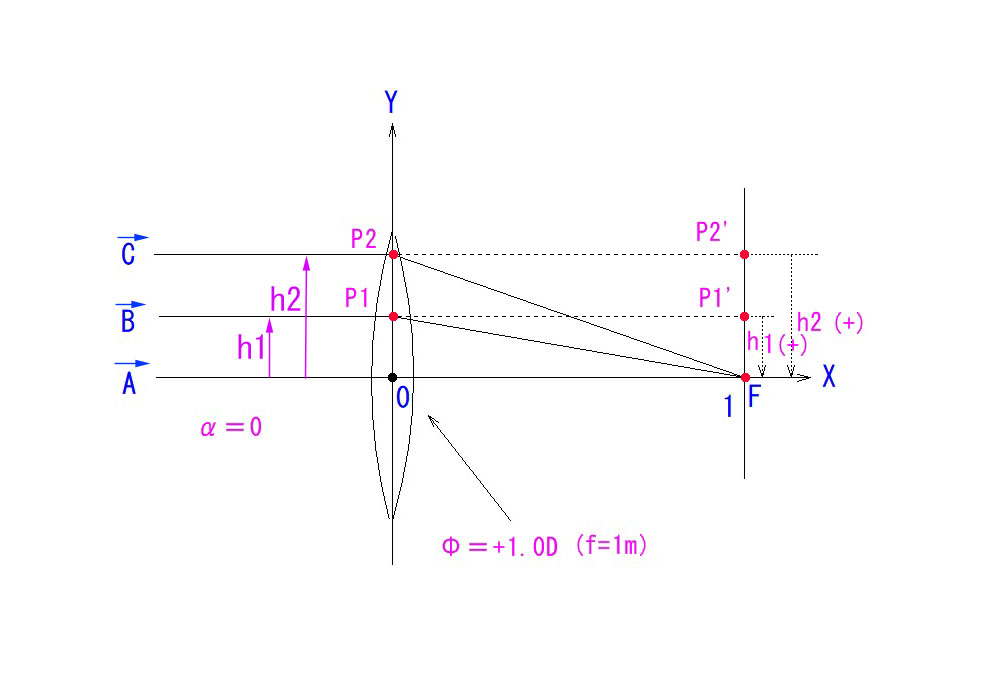
上図のように、平行光線 A, B, C が全て F に結像するのが、理想結像です。
今回も、レンズは厚みが無視できる、度数Φ=+1.0(焦点距離=1.0m)の凸レンズとします。
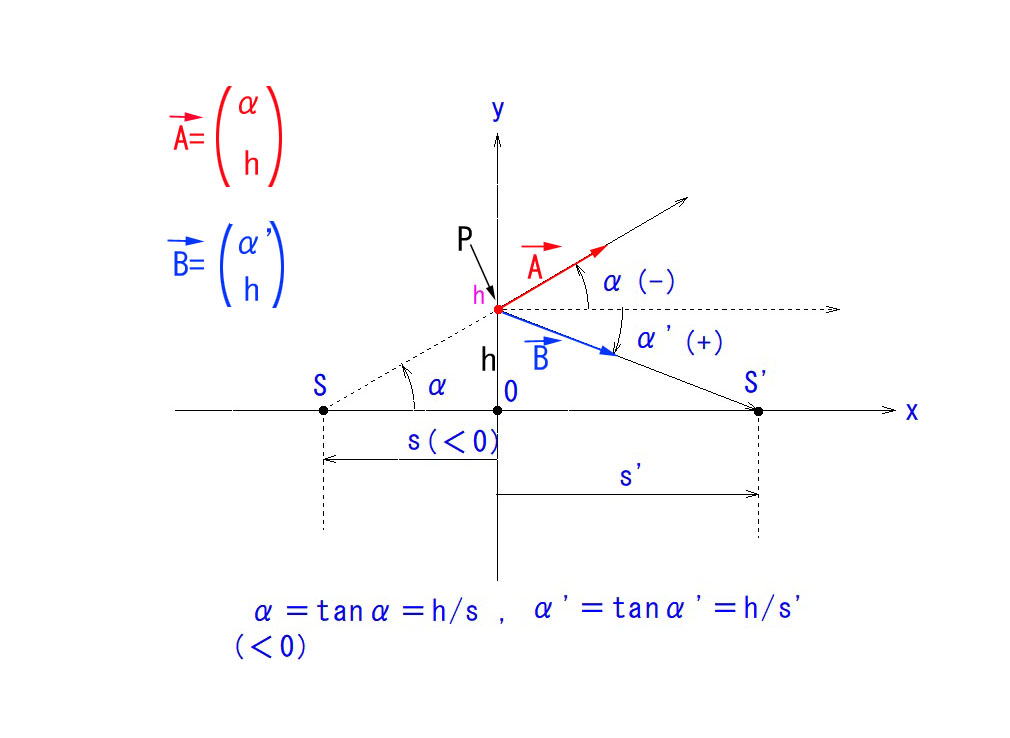
Φ=1.0Dとしたのは、光線傾角 tangent の分母が常に1になり、傾角要素のαが、α=tanα=h となって、長さの要素として可視化できるためです。(αは、下向きが+で、上向きがーです。)
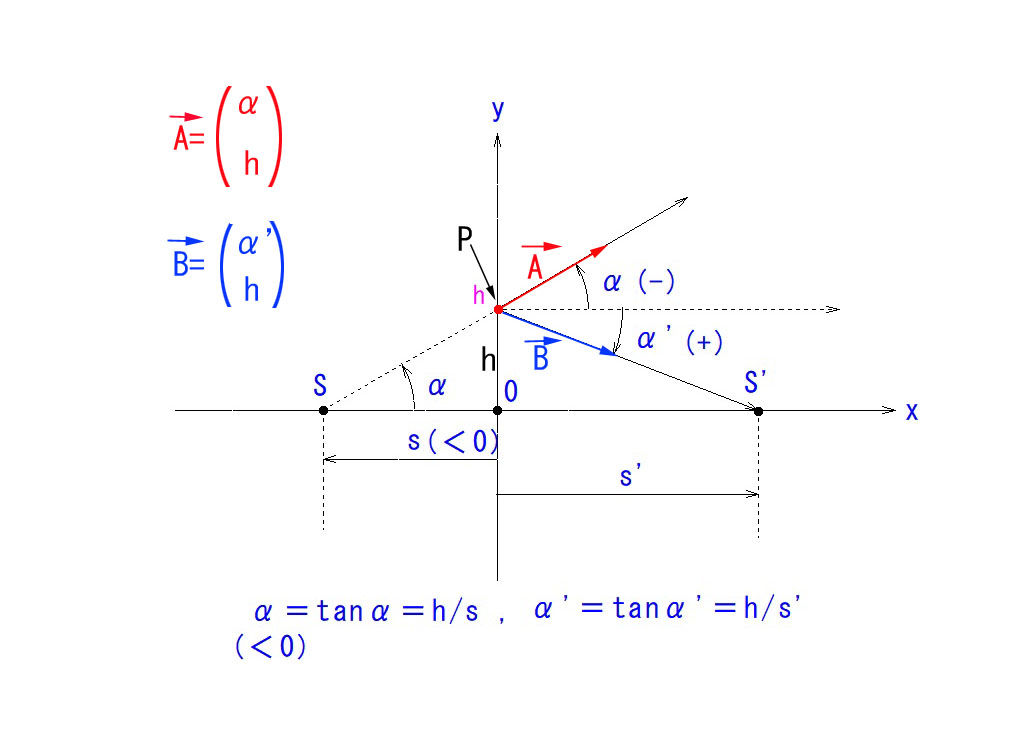
入射光線の傾角 α について、パワーΦの屈折面を高さ h で通過後に α’ となるとすると、
α’=α+hΦ (Φはレンズの度数、1/f ) となることについて、図に則してご説明します。
P2で光軸に平行に入射する光線 C は、傾角α=0,h=h2, Φ=1, を、それぞれ上式に代入すると、
α’=0+h2 = h2 となり、焦点 F でX軸と交わります。
光線 B も同様に計算できます。(α’=h1)
光線は、屈折点Pで、レンズの度数と、光軸からの屈折点の高さに比例した角度で折れ曲がるということです。(α=tanα で定義された屈折角度) 上例は、入射角 α=0ですが、α の値とは無関係に、屈折面に突入する高さhでの光線の折曲がり角度(α=tanα で定義された屈折角度)は一定なのです。
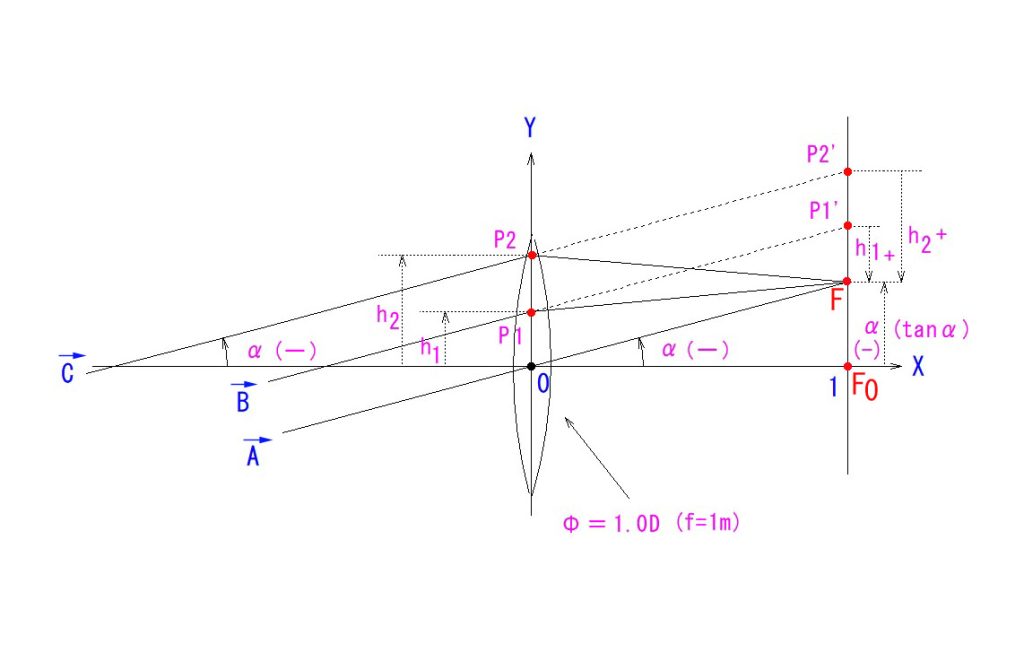
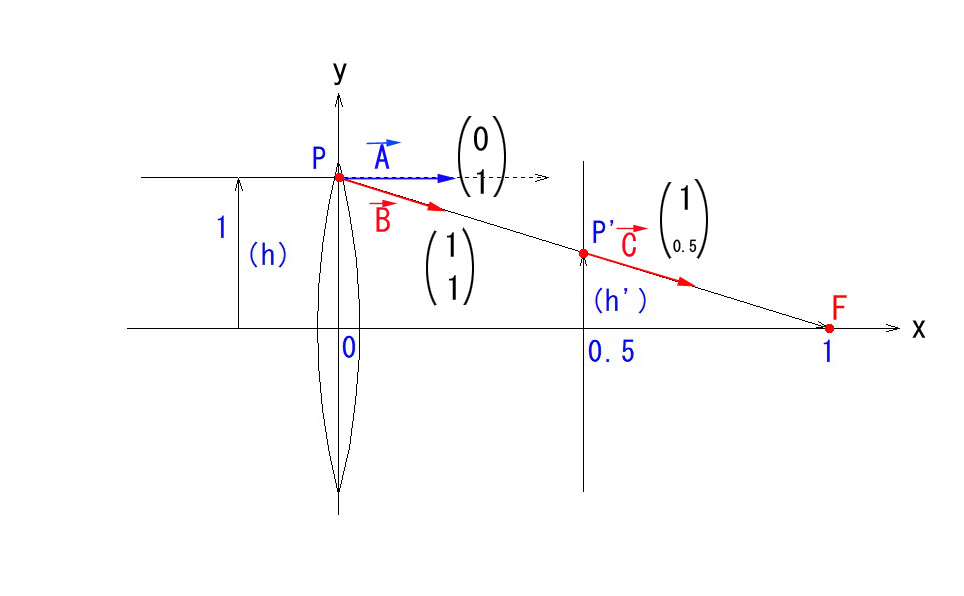
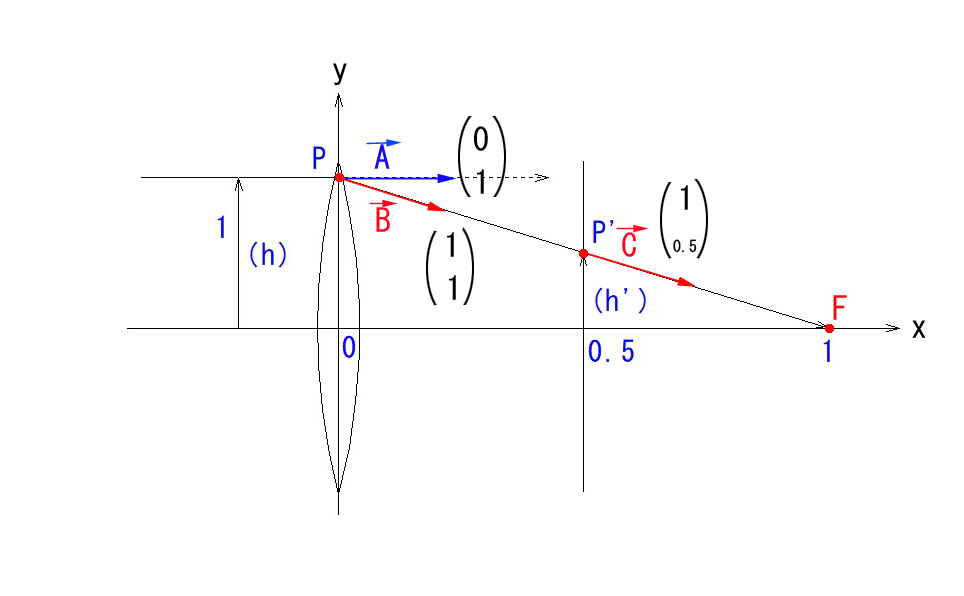
先ほどは、入射角 α=0 の特殊なモデルでご紹介しましたが、上図のようなケースも、全く同様にご説明できます。
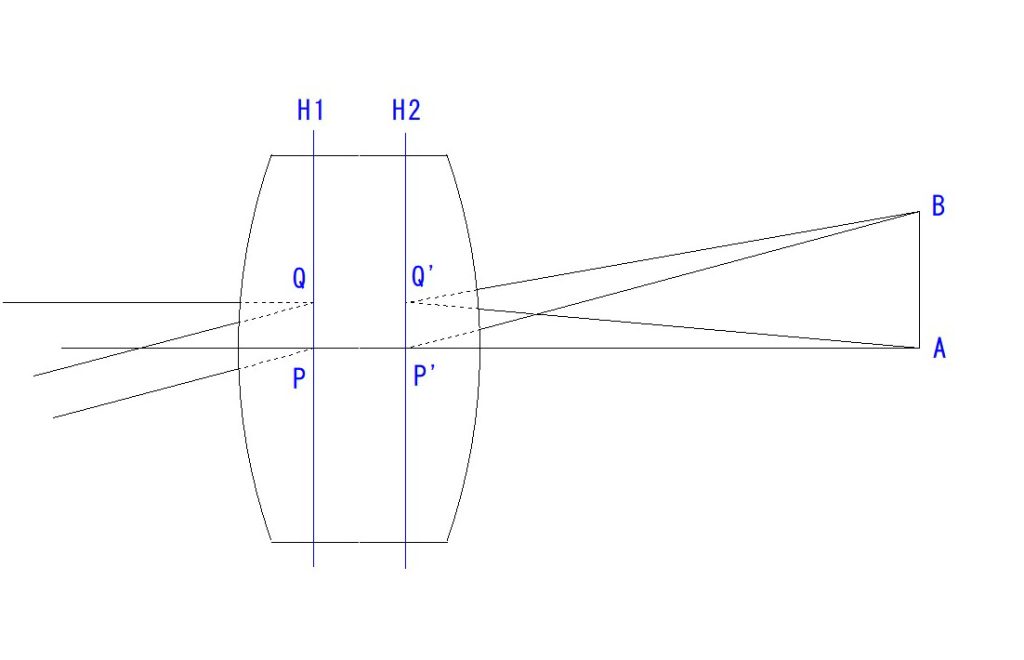
入射光線 B についてご説明しますと、P1で屈折しない場合は、P1’に到達しますが、屈折により、P1’→Fに移動するわけです。
お気付きと思いますが、αもα’も、通常の角度ではなく、tanα で定義されているところが重要です。
この図でも、α’=α+hΦ となっていることがお分かりになると思います。
理想の薄レンズに入射する光線は、「レンズ上の入射点の高さ h とレンズの度数 Φ に比例した角度で曲がり、それは入射光線の傾角に依存しない。」—ということです。(ただし、角度は下向き “tangent”で定義された値。)
* h の初期値には、全く制限がなく、どんな数字を入れてもかまいません。(計算に好都合な初期値で良い);
繰り返しになりますが、
α’=α+hΦ
h’= h
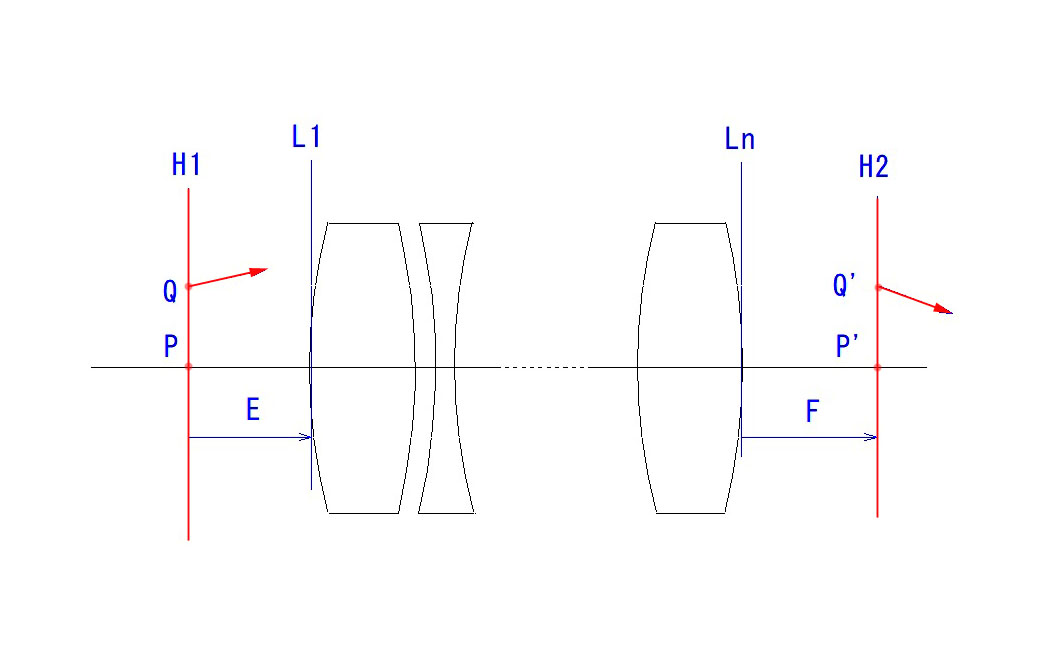
これを行列表記すると、こうなります。↓
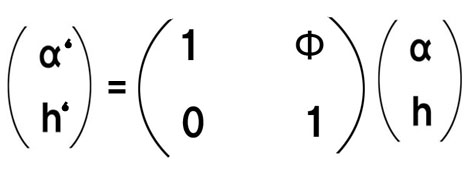
また、2つの屈折面に挟まれた空間は屈折せずに直進するため、αは変化せず、h のみが変化します。
通過間隔(光の進行方向=+)= t とすると、
α’=α
h’= h – αt
これを行列で表記すると、こうなります。
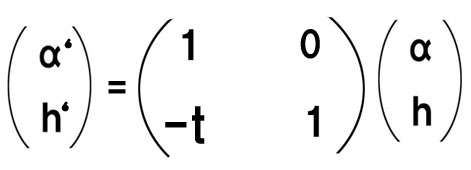
どんなに複雑に見える光学系も、屈折マトリックスと移行マトリックスを次々に掛け合わせることで、その全系のシステムマトリックスが得られるわけです。結果として得られたシステムマトリックスの行列式の値も1です。
*一見、通常の平面上の幾何学的ベクトルと混同し勝ちですが、そうではありません。
α、α’はx座標ではなく、その光線の基点に於ける傾角(特別に定義された)です。