代数的考察には踏み込まない、と一旦申しましたが、シンプルな方法が閃いたので発表させていただきます。
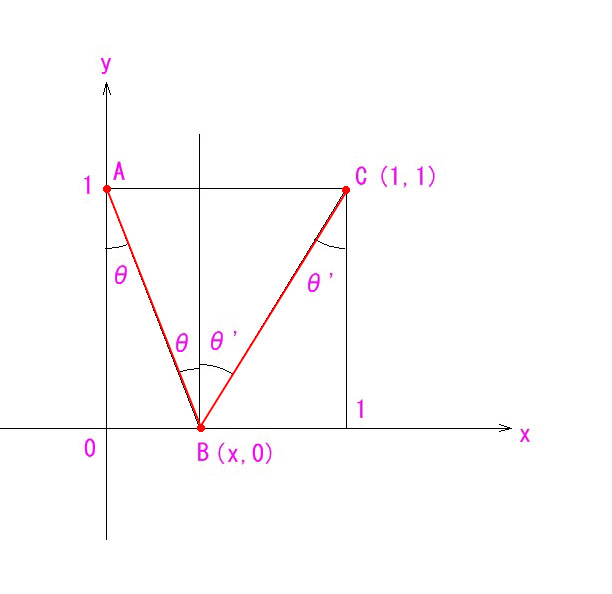
　まずは、反射の法則から・・・。
　通常は、AB = √(x^2+1) , BC = √｛(1-x)^2+1｝から、f(x)=√(x^2+1)+√｛(1-x)^2+1｝を微分して法則を導き出すのですが、証明したい法則は θ = θ‘ なので、最初から三角関数を用いた方がシンプルになります。
AB + BC = 1/cosθ + 1/cosθ‘ —– f(θ)
　　と、総光路長が非常にシンプルに表せられます。

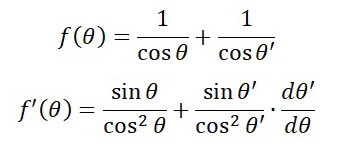
θ で微分すると、上記のようになります。
dθ’/dθ が邪魔物ですね。
そこで、もう一つの関係式、tanθ + tanθ’ = 1　の両辺を微分してみます。

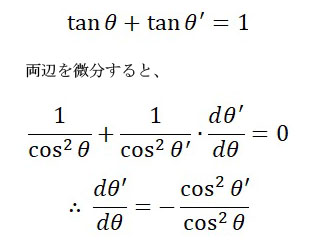
これで、最初の f'(θ) の式から、dθ’/dθ を消去できます。

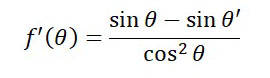
　厳密には、これをさらに微分するのですが、今回は割愛して、0＜x＜1 の間に解が一つある前提で進めます。
f'(θ) = 0 のときに、f(θ) が最小値になるので、
　　　　　sinθ = sinθ’ 、すなわち、θ = θ’ が導けました。

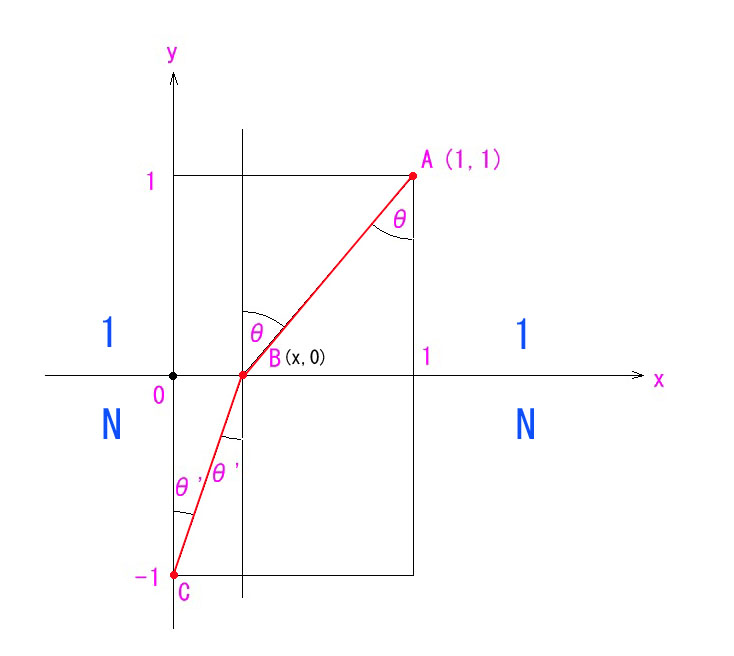
屈折の法則も、同様の方法で導けます。

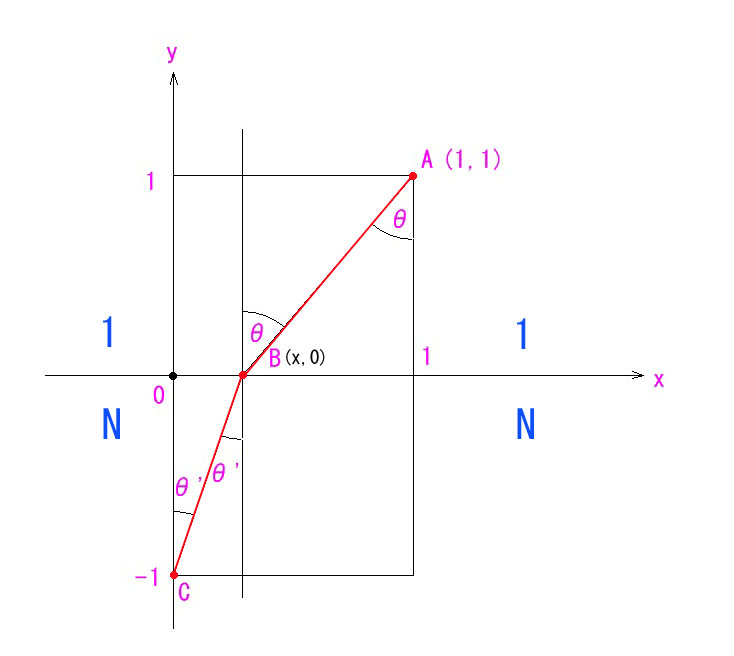
　反射の例との違いは、Y 軸の負領域と正領域で屈折率が違うということです。
上図では、Y 軸の正領域は空気中で屈折率1，負領域の屈折率をNとしています。
光の速度は屈折率に反比例するので、同じ距離でも、Y軸の負領域では、時間がN倍かかるわけです。
Y軸の正領域の速度がN倍、と考えても同じことです。
　従って、最小所要時間の経路を求めるには、Y軸の負領域の光線の長さを最初からＮ倍して考察することになります。
AB + BC = 1/cosθ + N/cosθ‘ —– f(θ)

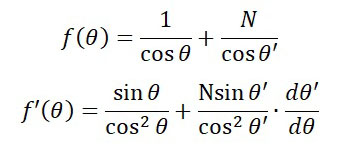
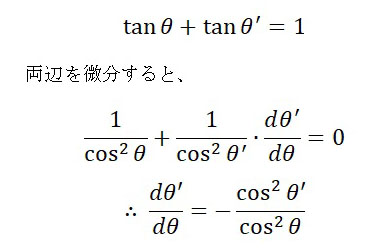
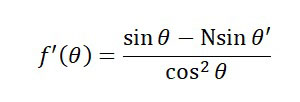
先程と同様に、f'(θ) = 0 のときに、f(θ) が最小値になるので、
sinθ = Nsinθ’　　が導けました。

　いかがでしょう？　反射と屈折で数式がほとんど同じですね。
以上から、反射面は光線の向きが反転することも考慮して、屈折率＝”-1″の特殊な屈折面として、通常のレンズの追跡方法に一般化出来ることが分かりましたね。