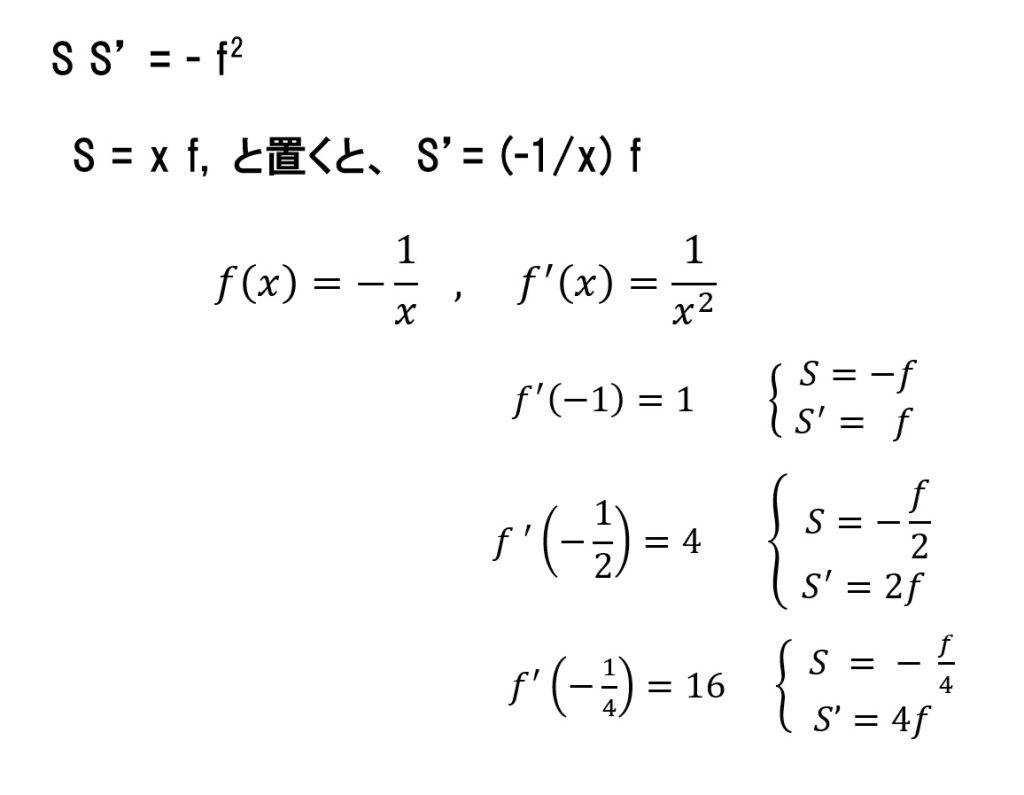
行列を用いた近軸光線追跡や、主点位置の算出について、不慣れな方が多いと思い、追加説明をさせていただきます。
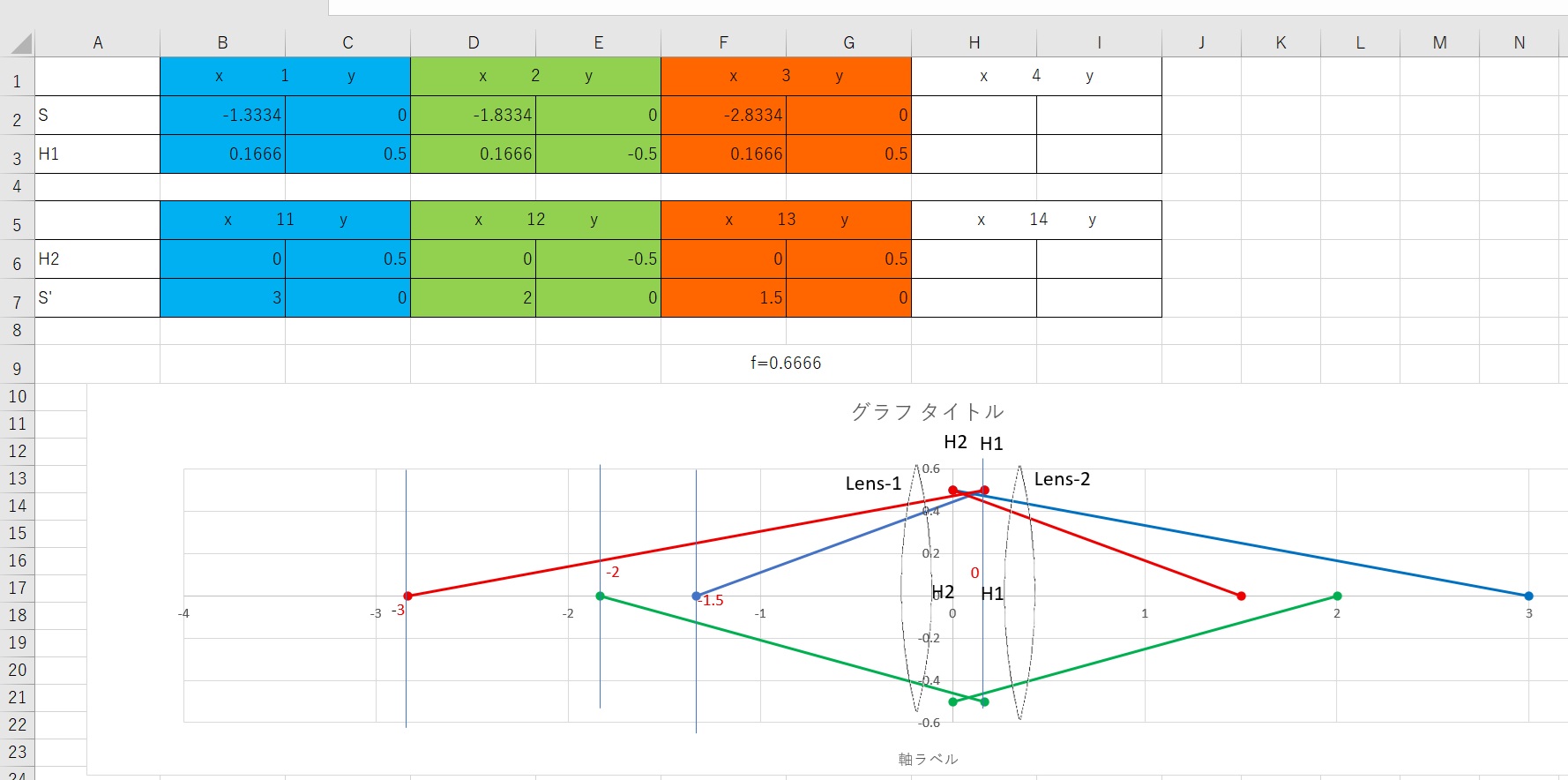
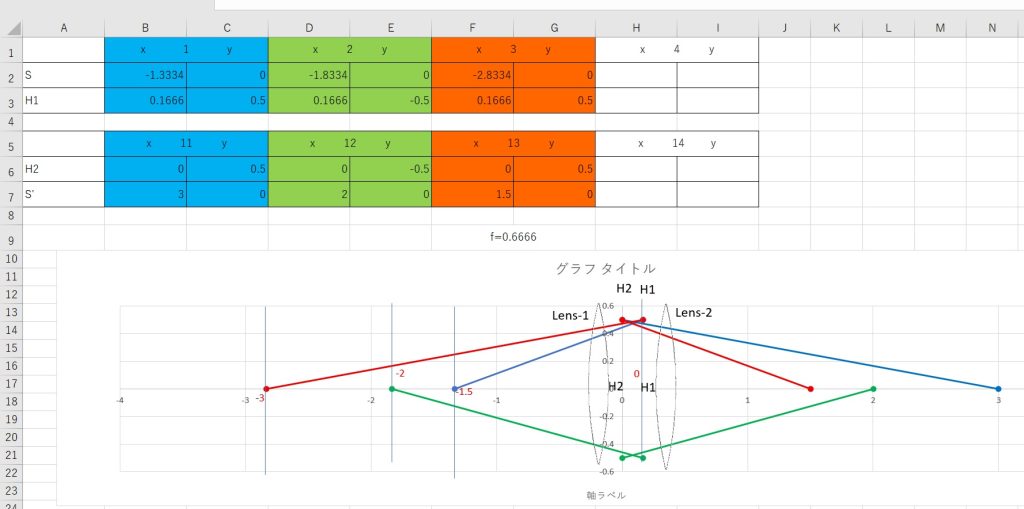
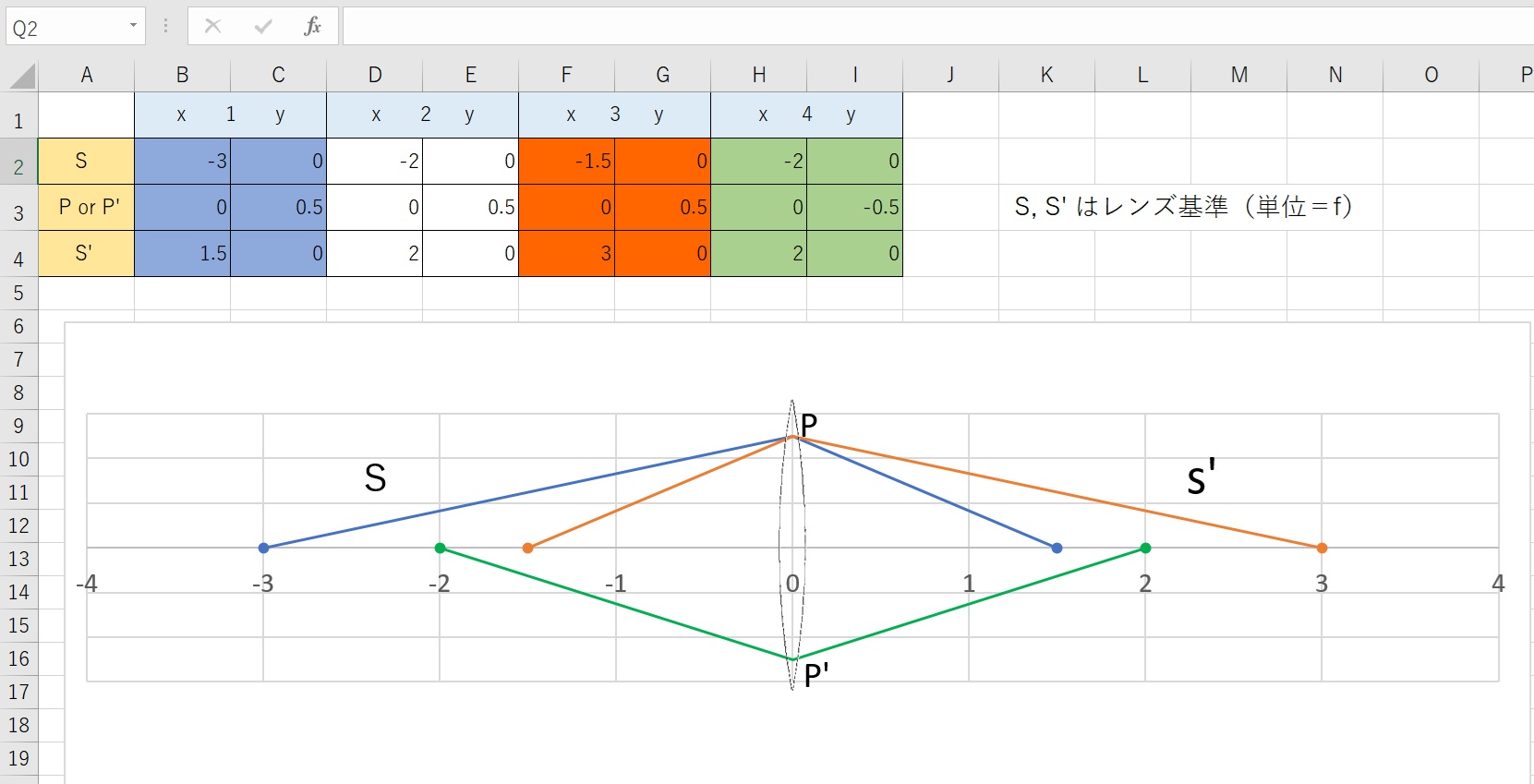
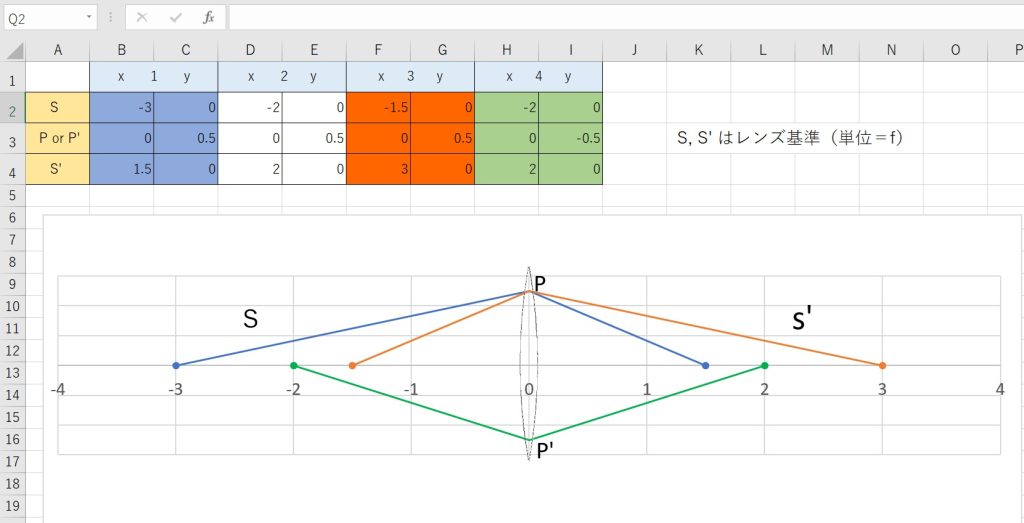
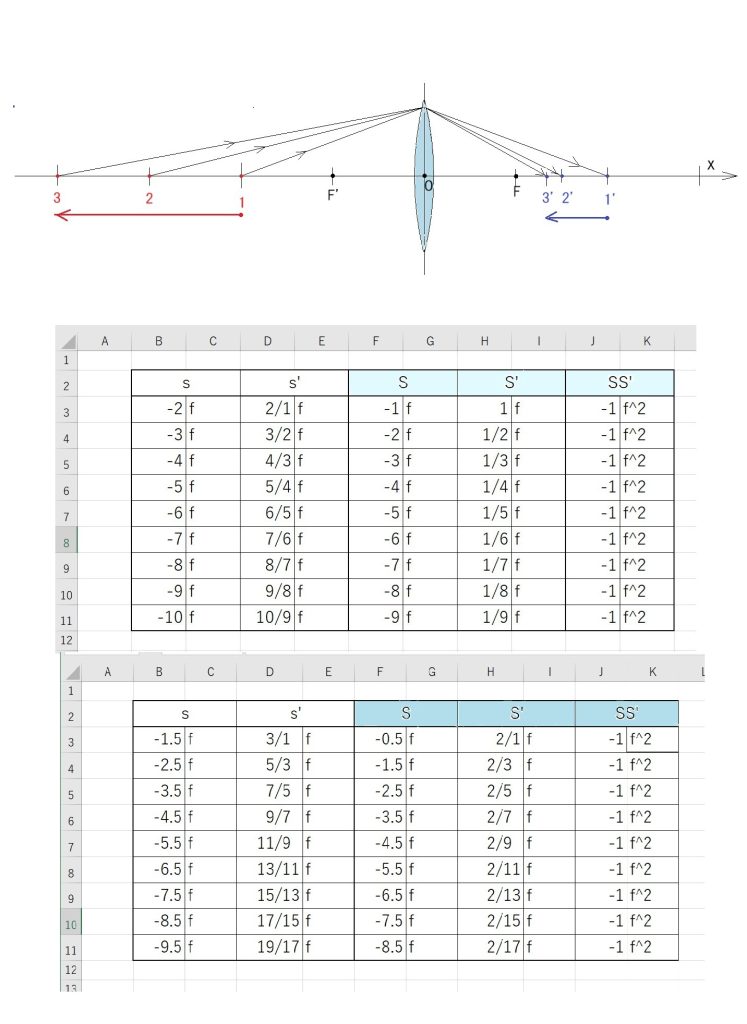
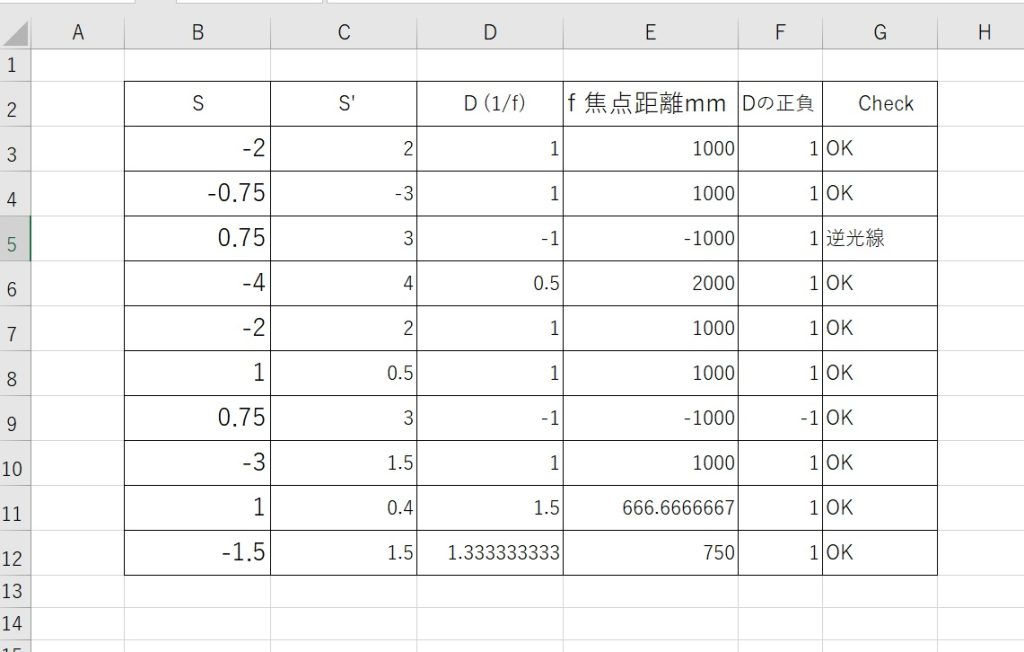
まず、レンズ系のモデルは、+1.0D の薄い凸レンズを2枚、0.5mの間隔で保持した、シンプルなものです。 シンメトリックな光学系なので、両主点位置も対称配置になります。
薄レンズは、シンプルな屈折マトリックスで表現できます。
レンズ間隔は、これもシンプルな移行マトリックスで表現します。
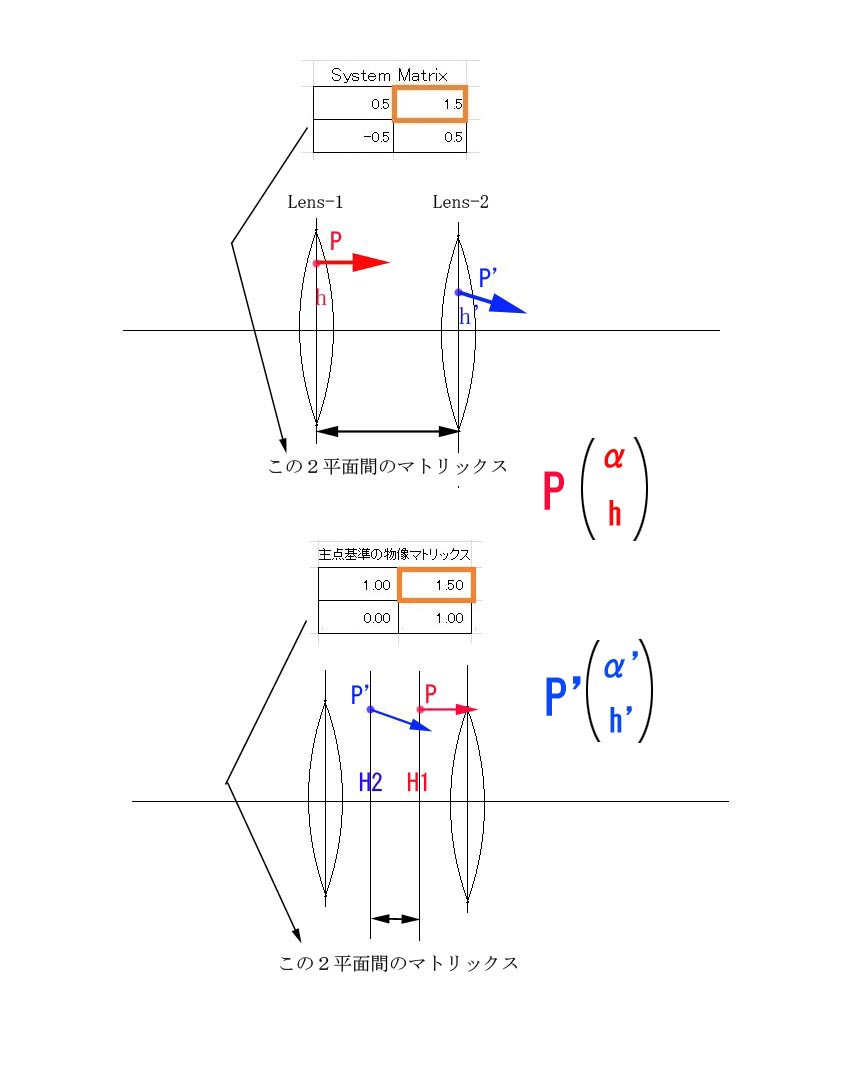
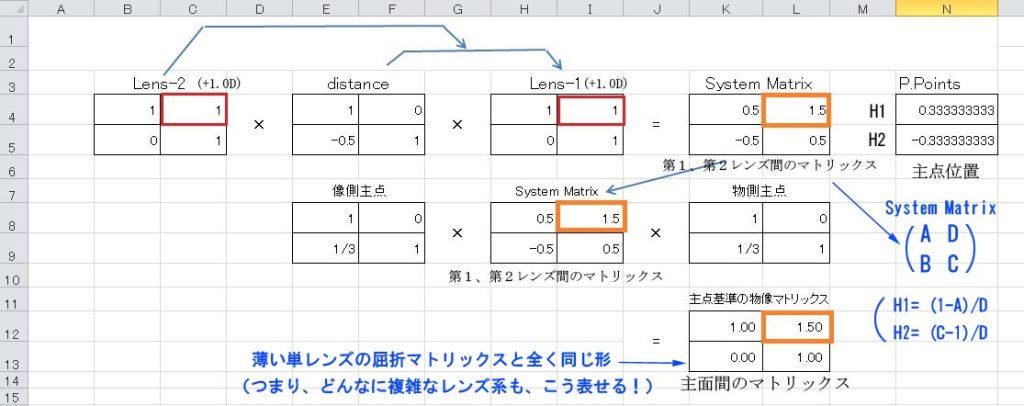
まず、単純に、レンズ1の屈折マトリックスにレンズ間隔の移行マトリックスを掛け、それにレンズ2の屈折マトリックスを掛けると、レンズ1~レンズ2の間のシステムマトリックスが得られます。
そのシステムマトリックスから、主点位置が簡単に求まります。
さらに、そのシステムマトリックスを挟むように、両主点位置の移行マトリックスを掛けると、両主面間の別のシステムマトリックスが得られます。 何と、それは薄レンズの屈折マトリックスそのものになります。
システムマトリックスは、計算途中を含め、右上の要素が常に合成パワーになり、行列式の値は常に1です。
今回は、ご参考のために、主点基準のシステムマトリックスの導出をお示ししましたが、実は、この計算は全く不要で、合成パワーが最初のシステムマトリックスで分かれば、それを単レンズのパワーとして、屈折マトリックスを組めば良いのです。
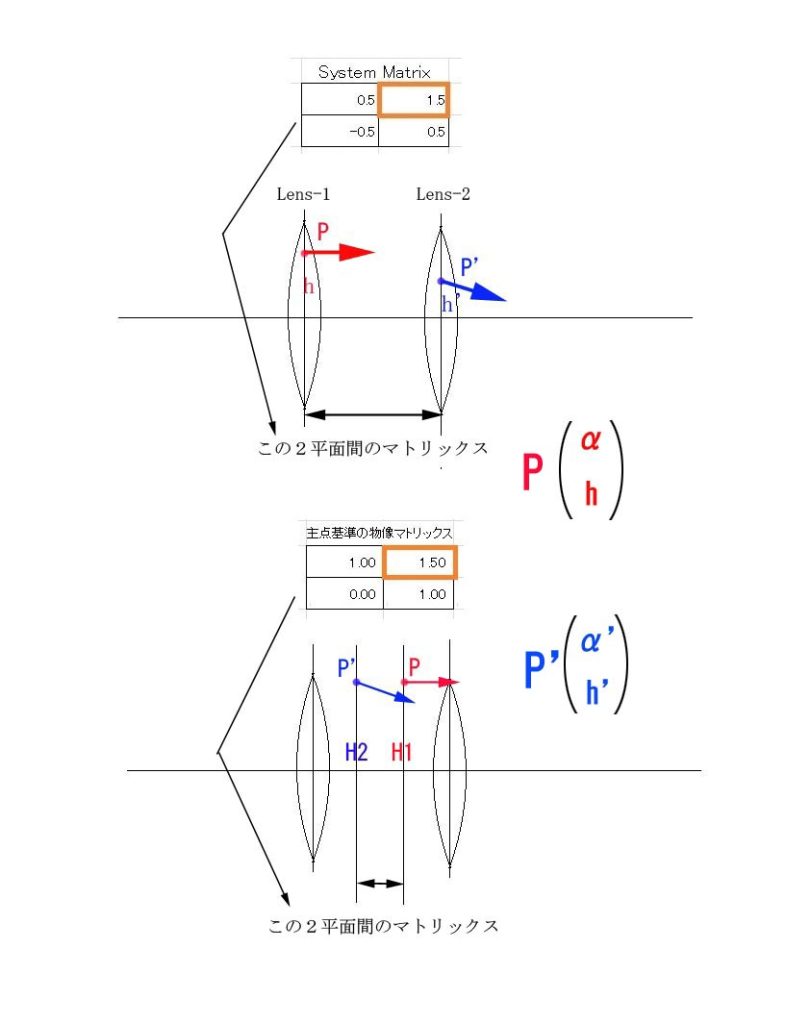
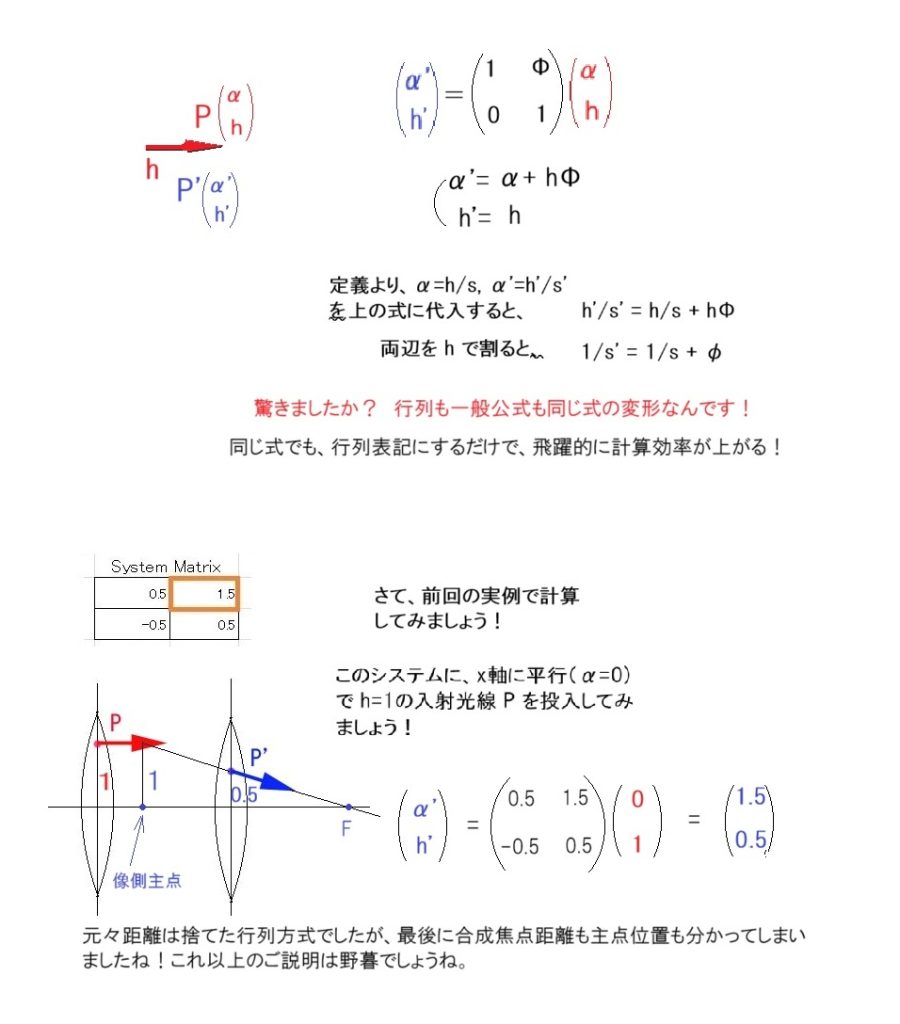
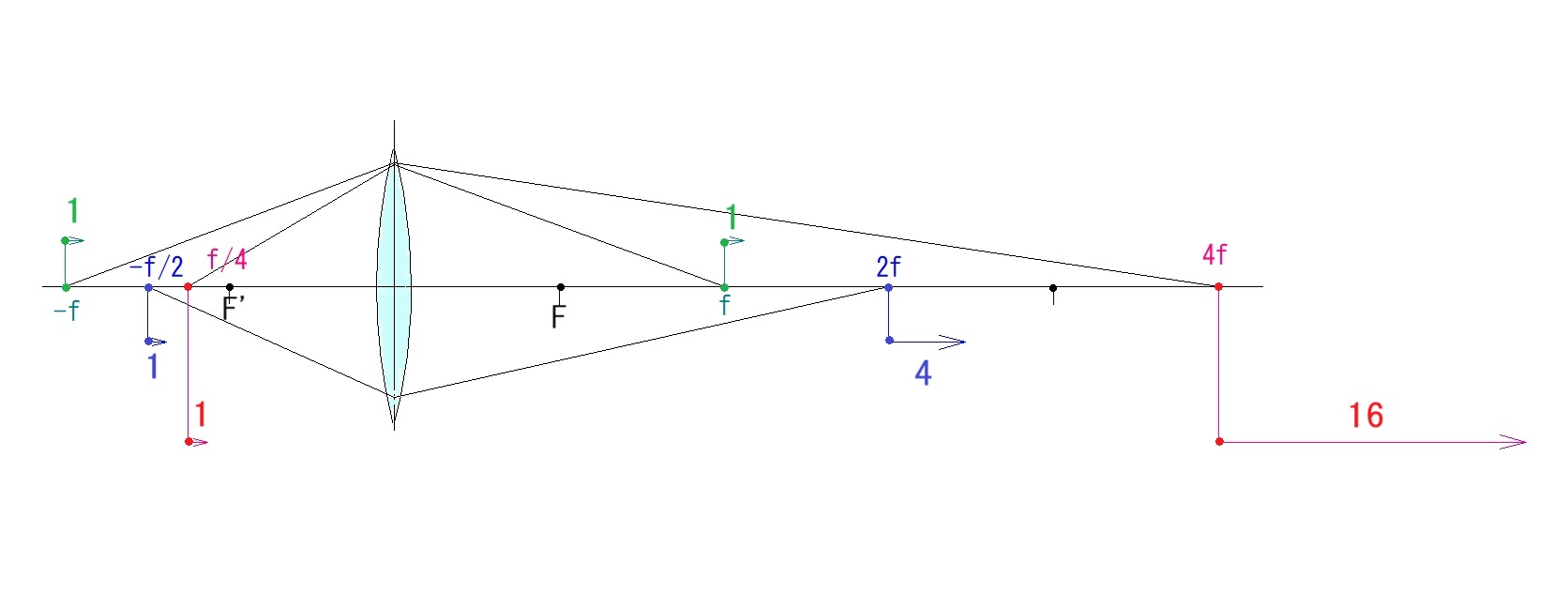
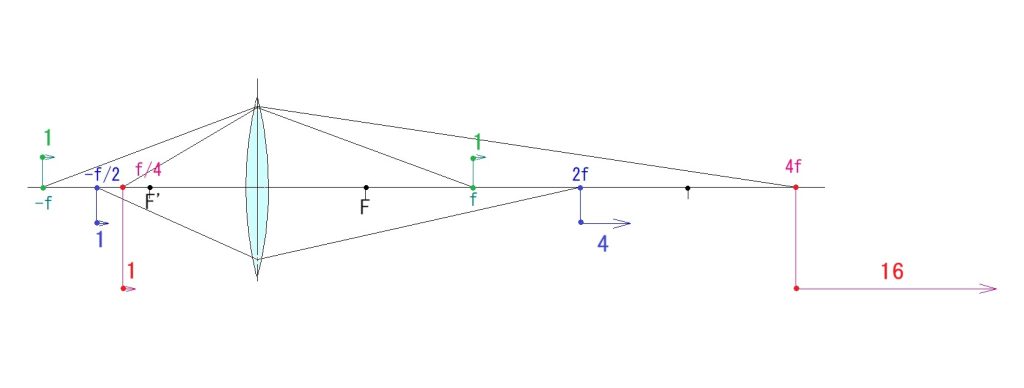
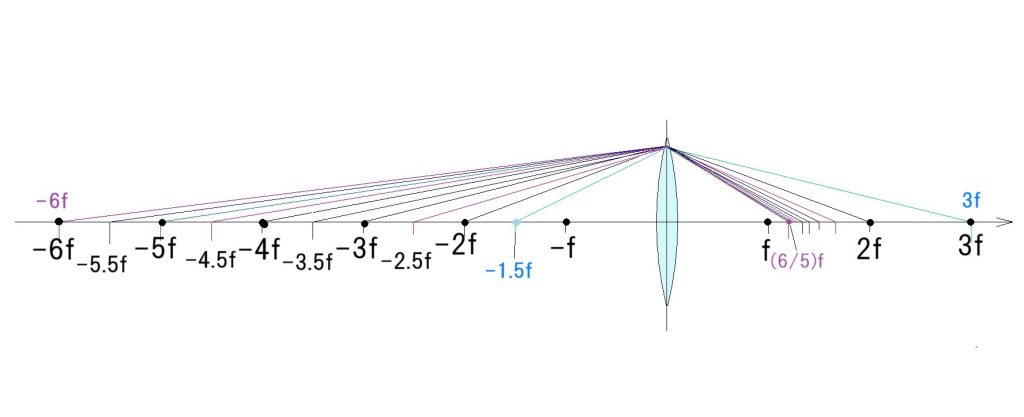
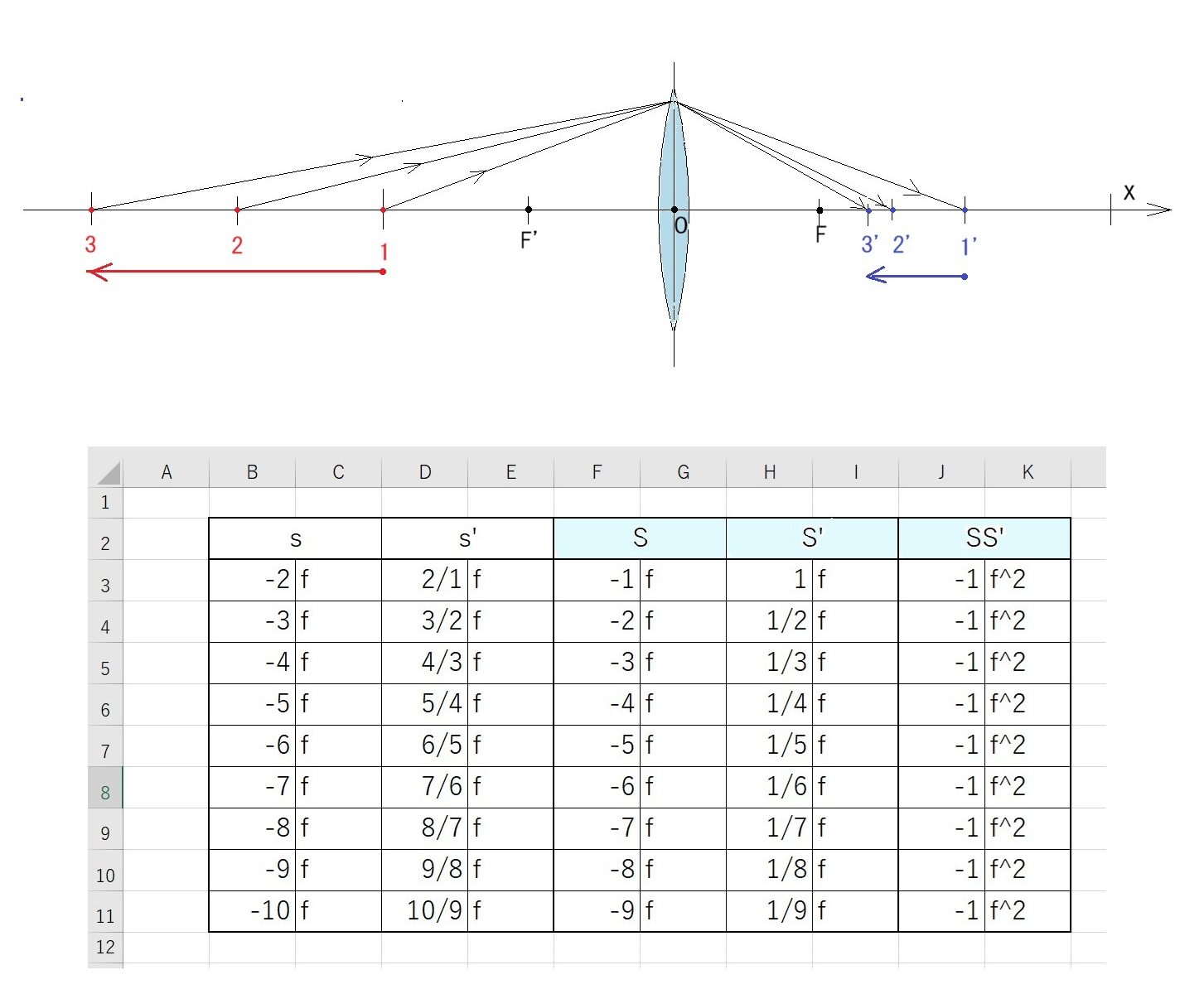
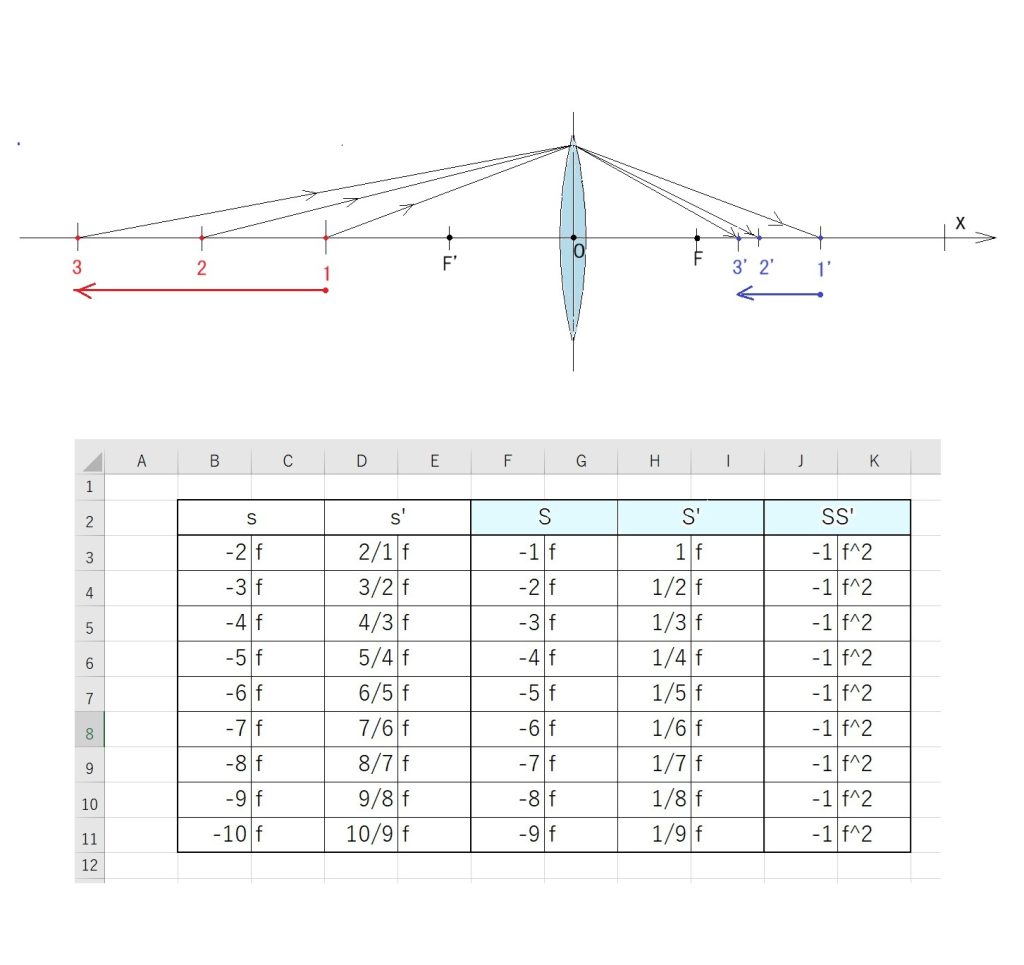
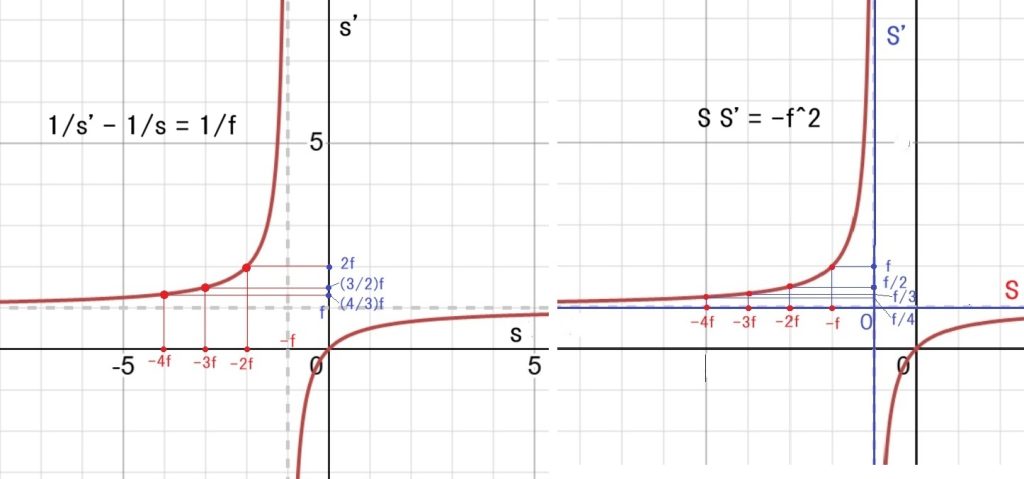
一般的な結像公式(1/s’ – 1/s = 1/f ) は、3つの向きを持った距離同士の関係式ですが、
行列の方法は、距離を問題にせず、指定した2面間を通る光線の通過点に於ける光線のx軸方向に対する傾き(α)と、その点の高さ(h)を求めます。 当初は、何でわざわざ?と思うでしょうが、一般的な結像式は、単レンズの光線追跡には有効ですが、レンズ枚数が多くなるほど、計算が複雑になるのです。行列の方式だと、何個でもその構成行列を掛け合わせることが出来るのです。
システムマトリックスは、指定した第1の面上の P から、もう1つの面の P’ を得るための行列です。
興味を持たれた方は、今までの屈折マトリックス等の関連記事を今一度ご参照いただけると、よりご理解が深まるかと存じます。