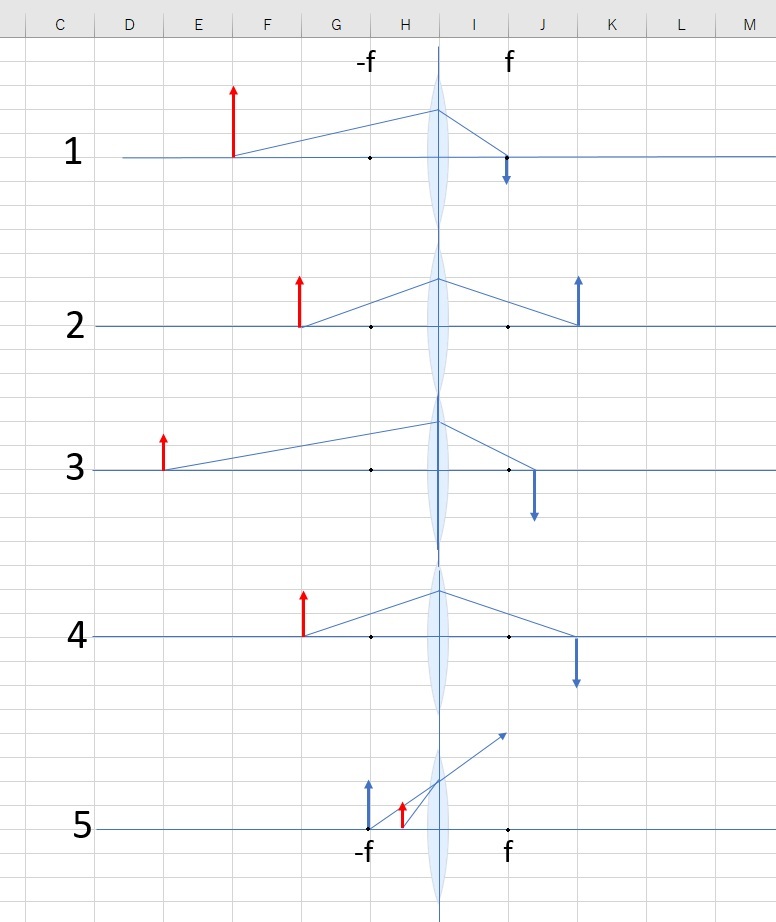
問題: 上の1~5 の光路図で、間違っている物(番号)を全て挙げよ!
* セルの横幅= f とします。
* 赤い矢印が物体で、青い矢印が像です。5は、虚像です。
* 光線はヒントになり過ぎるので、敢えて最小限に省いています。
その代わりに、セルの罫線がヒントになります。

Innovation of Astronomical Telescope
正立ミラーシステム(EMS)を開発した松本龍郎のサイト。 たった2回の反射で天体望遠鏡の像を正立像にします。
Tatsuro Matsumoto; Inventor of the EMS, Erecting Mirror System. EMS offers non reversed upright image with no additional undesirable abberations.
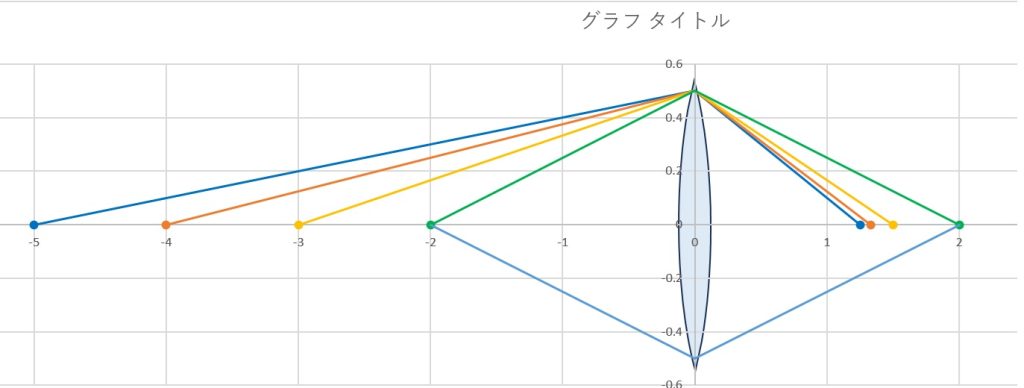
Lens shape in the optical diagram of paraxial imaging is not so important. But the lens shape in the diagram will definitely enhance the intuitive understanding of the readers. And the beautiful lens shape will add value to the diagram.
I have been struggling with this issue, drawing a beautiful lens shape, with Excel for a whole day and night, in vain.
The issue made me feel tired and sleepy this morning!
I asked my nurses for the solution of this issue with Excel this morning in vain, but after 15 minutes, my attending physician kindly came to my room, and She was able to show me the perfect solution in Excel almost instantly!!
Above is the best lens shape I could make with the help of my loving Doctor!
近軸光線追跡は、レンズの厚さを”0”と想定しており、光路図にレンズ形状を挿入することは、さほど重要ではありませんが、読者の直感的な理解のためと、光路図自体の審美性には、欠かせません。
寝不足で、憂鬱な朝を迎えた今朝でした。
エクセルに長けた看護師さんが2名ほど来てくれても解決せず、半ば諦めていたところ、15 分後に、何と、主治医の先生が病室に来てくれ、すいすいと、ほぼ一瞬で感激の解決! 上図が、それでゲットした、今までで一番綺麗な ”レンズシェイプ” を挿入した、初めての光路図です。 これで、下がっていた免疫値も回復しそう!LOL
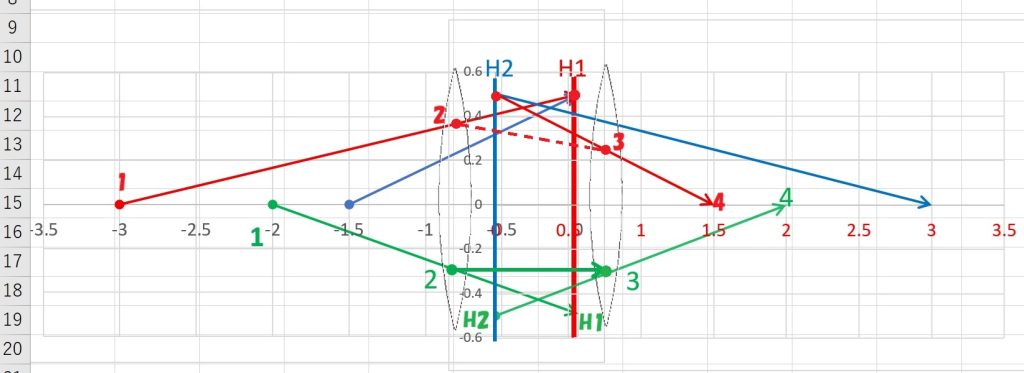
順番が交叉した両主面について、全くご質問がないので、先回りしてご説明します。
当初は、物空間にあるのが物側主点で、像空間にあるのが像側主点だと思うのが自然ですからね。初学の段階で、交叉した主点(主面)関係を見せつけられたら、真面目に取り組んでいた方ほど、頭をガーンと殴られたような衝撃があったはずです。(私も当初はそれで悶絶しましたから。)
初めて交叉した主面の光路図を見せられたら、光線が両主面間で折り返しているのか?と思ってしまう方もいるかも知れません。
そうした方に安心していただくため、あるいは、勉強の継続を断念してしまった方を呼び戻すために、少々ややこしい作図 ↑ をしてみました。
分かりやすく可視化したつもりで、図から直感的にご理解いただけると思っています。
赤と緑の系列だけに、実際の光路 (1→2→3→4) をお示ししました。光線自体は、両主面上の H1 も H2 も通るわけではなく、そこ(H1)に向かって、そこ(H2)から出て行く、というものです。(H1,H2 はそれぞれ、虚物点と虚像点ですから。)
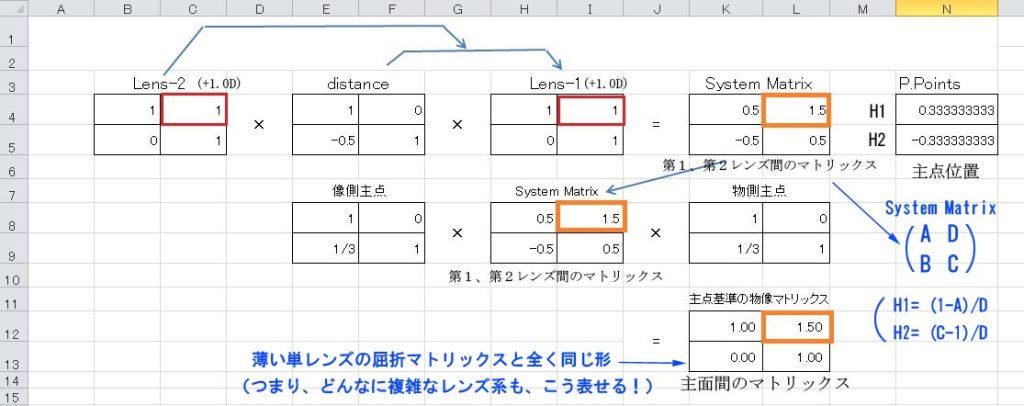
行列を用いた近軸光線追跡や、主点位置の算出について、不慣れな方が多いと思い、追加説明をさせていただきます。
まず、レンズ系のモデルは、+1.0D の薄い凸レンズを2枚、0.5mの間隔で保持した、シンプルなものです。 シンメトリックな光学系なので、両主点位置も対称配置になります。
薄レンズは、シンプルな屈折マトリックスで表現できます。
レンズ間隔は、これもシンプルな移行マトリックスで表現します。
まず、単純に、レンズ1の屈折マトリックスにレンズ間隔の移行マトリックスを掛け、それにレンズ2の屈折マトリックスを掛けると、レンズ1~レンズ2の間のシステムマトリックスが得られます。
そのシステムマトリックスから、主点位置が簡単に求まります。
さらに、そのシステムマトリックスを挟むように、両主点位置の移行マトリックスを掛けると、両主面間の別のシステムマトリックスが得られます。 何と、それは薄レンズの屈折マトリックスそのものになります。
システムマトリックスは、計算途中を含め、右上の要素が常に合成パワーになり、行列式の値は常に1です。
今回は、ご参考のために、主点基準のシステムマトリックスの導出をお示ししましたが、実は、この計算は全く不要で、合成パワーが最初のシステムマトリックスで分かれば、それを単レンズのパワーとして、屈折マトリックスを組めば良いのです。
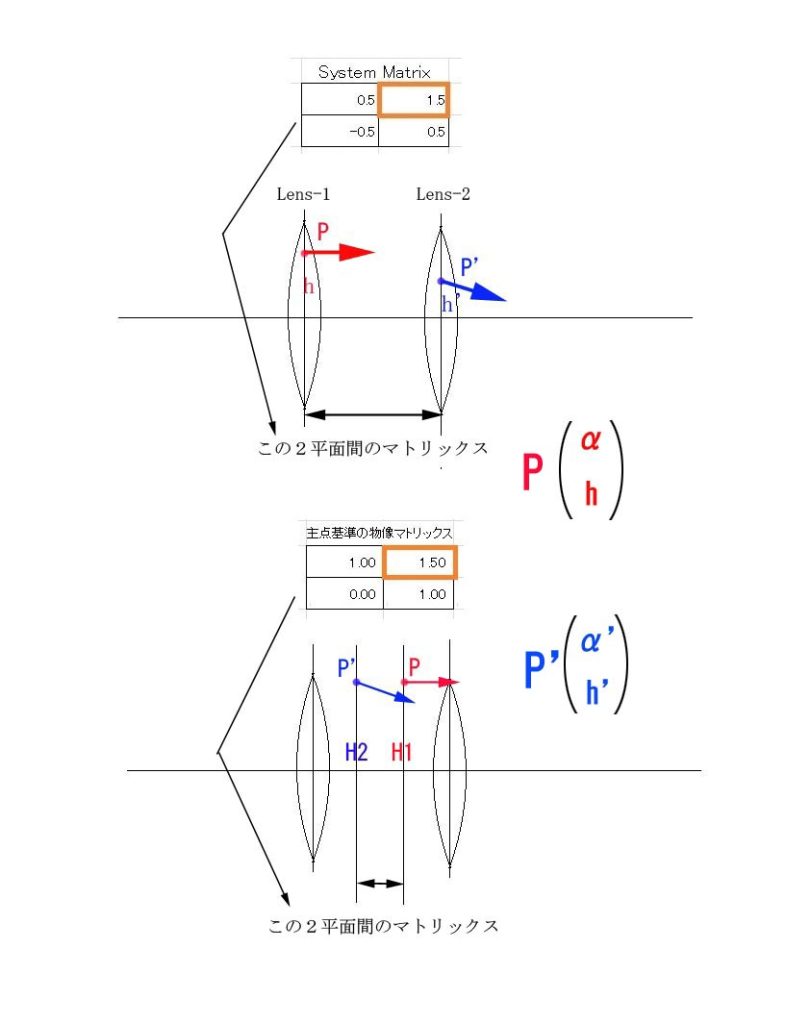
一般的な結像公式(1/s’ – 1/s = 1/f ) は、3つの向きを持った距離同士の関係式ですが、
行列の方法は、距離を問題にせず、指定した2面間を通る光線の通過点に於ける光線のx軸方向に対する傾き(α)と、その点の高さ(h)を求めます。 当初は、何でわざわざ?と思うでしょうが、一般的な結像式は、単レンズの光線追跡には有効ですが、レンズ枚数が多くなるほど、計算が複雑になるのです。行列の方式だと、何個でもその構成行列を掛け合わせることが出来るのです。
システムマトリックスは、指定した第1の面上の P から、もう1つの面の P’ を得るための行列です。
興味を持たれた方は、今までの屈折マトリックス等の関連記事を今一度ご参照いただけると、よりご理解が深まるかと存じます。
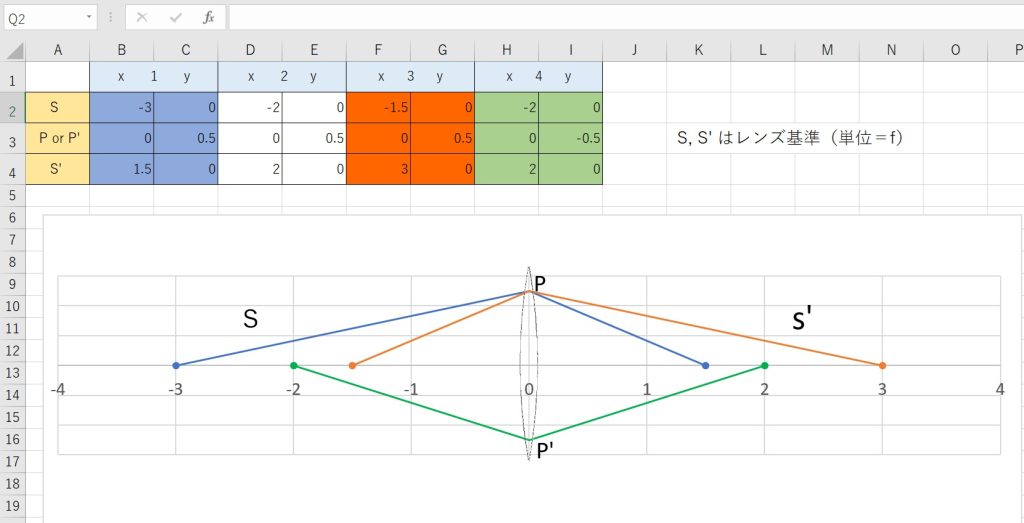
先日投稿した光路図は、S,S’ のデータ表(エクセル)から製図ソフトで線画を描き、それをプリントスクリーンしたものをPAINT(Windows アプリ)で装飾(編集)していました。
エクセルで表作成→製図ソフト→PAINT の順です。
慣れて来たのもあり、さほどの手間でもなかったのですが、どうせエクセルで表を作るのだから、そのままエクセルで、それなりに説得力ある光路図は描けないものか?と、ネットを頼りに、苦手なエクセルとしばし、格闘!
レンズのアウトライン(背景削除、透かし)だけは、製図ソフトとPAINT を使いましたが、これは、後で何度でも使いまわし、複写が可能なので、お許しいただきたい。^^:
わざと表を見せているのは、エクセルならではの特権。^^
セルの色と光路図の光線のデータ系列の色調を合わせました。
今まで、PAINT で意外に苦労していたのは、光線末端のドットの描画で、微妙な位置調整に何度も再トライしていました。今回のエクセルの散布図の描画では、同じデータ系列の光線の始点と終点にドットを簡単に打つことが出来ました。ネット検索のお陰で、自分では到底探せませんでしたが、何と、光線を矢印に変更する際の OPTION に先 ー● があったのです。
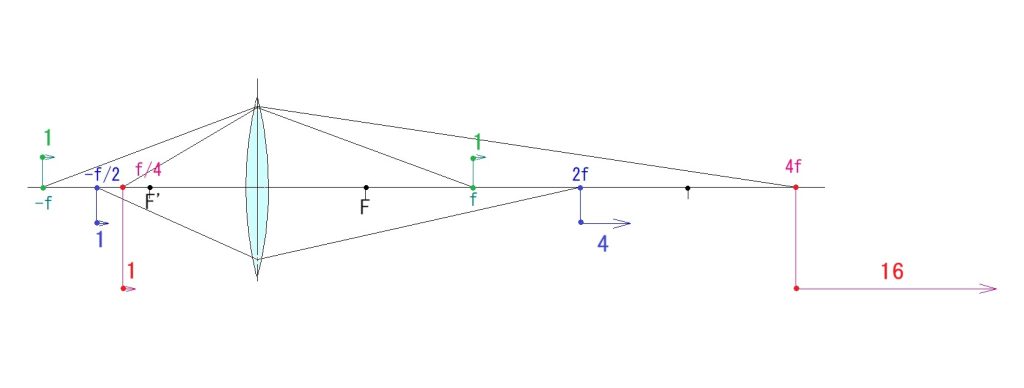
物点を -f → 0 (F’) に向けて速度Vで動かす時、像点の速度がその何倍で右に動くか?について検証してみました。
物点距離 S=-f , 像点距離 S’ = f の時、両点の速度は同じです。
物点距離 S=-f/2 , 像点距離 S’ = 2f の時、
像点の速度は 4 V となります。
さらに、物点距離 S=-f/4 , 像点距離 S’ = 4f の時、
像点の速度は 16 V となります。(ニュートン公式基準なので、物点距離、像点距離はレンズの両焦点から測定)
で、仮に S=-f/1000, S’ = 1000 f の時は、
像点の速度は、1000000 V (100万V)となるので、レンズに向けて弾丸を発射すると、弾丸の像は光速を超えます。
(f/1000)は、レンズの焦点距離が1000mmなら、1mmに相当します。焦点直前ですね。
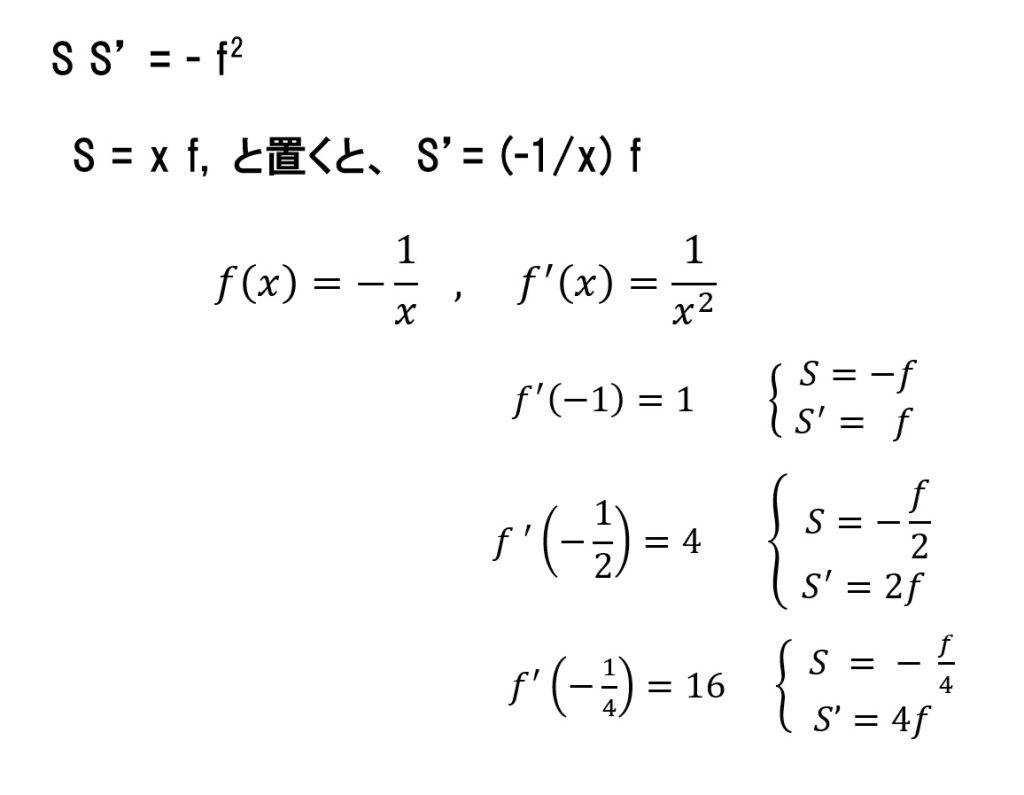
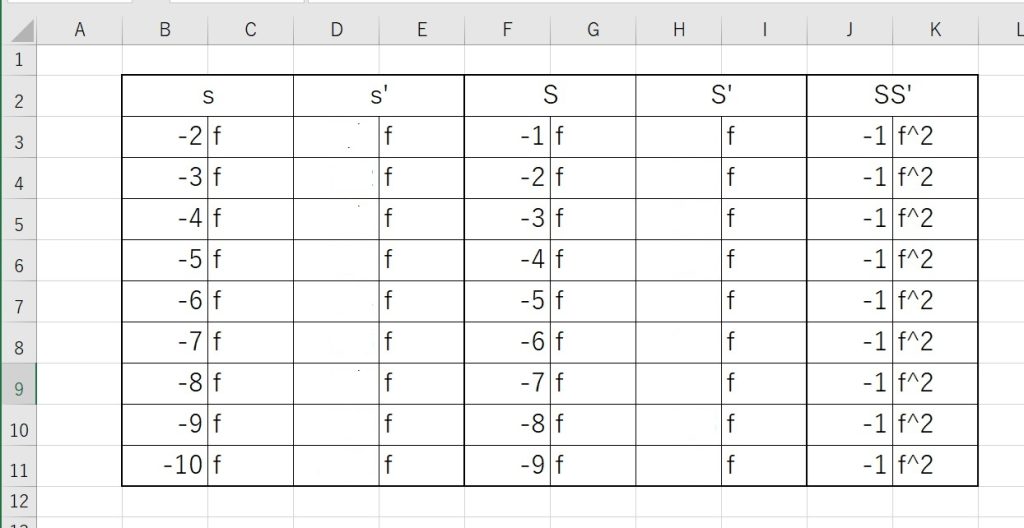
先日の、ニュートンの公式の検証についての講座が友人に不評で、原因を探っているところですが、前提のご説明が不十分だったのでは?と思い、少し、仕切り直しです。
いきなり整然とした計算結果表を見せ付けられても、威圧にしか取れない方もあったのかも知れません。
そこで、ほぼ計算前の表をお示しし、何をやろうとしていたのか?ということをまずは共有させていたくのが先決だと気付きました。
そして、結果として、(今後は)計算不要な法則が見つかった感激を、少しでも皆様とシェアさせていただけたら、大変励みになります。
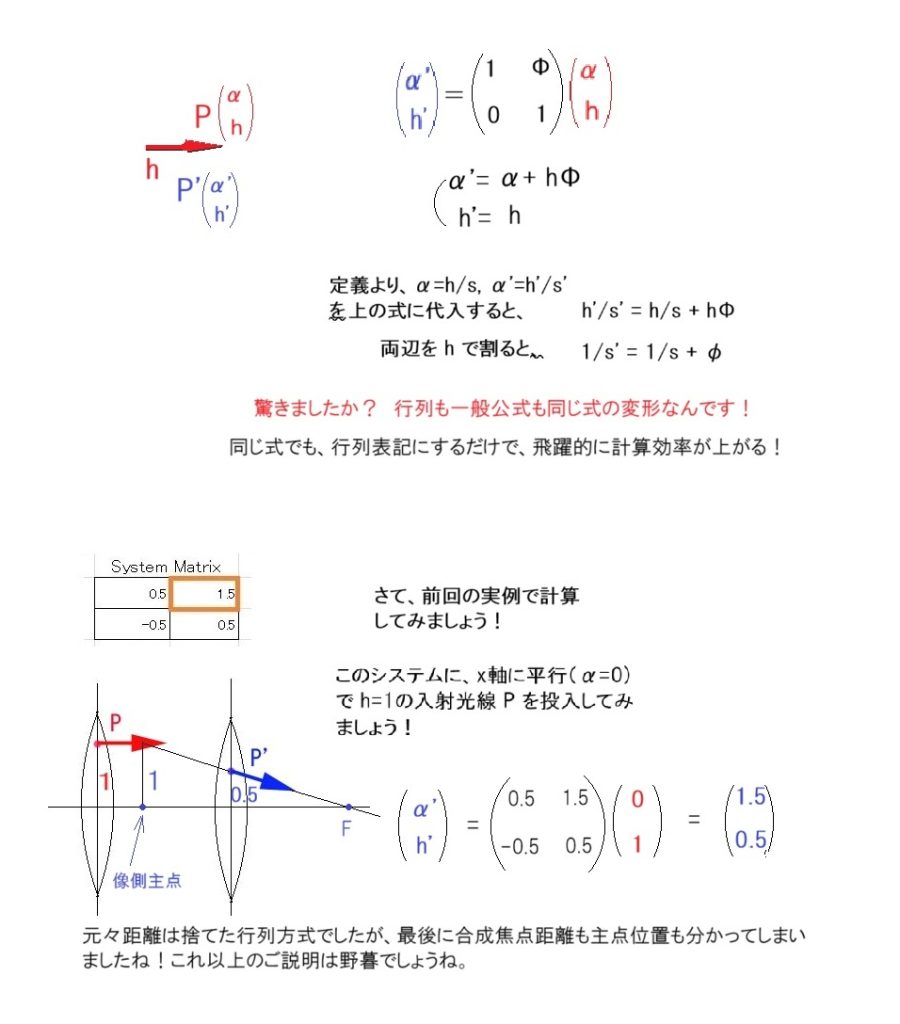
上の表は、これから何を求めるか?の最初の前提です。レンズの焦点距離= f に於いて、任意の物点距離 (s, S,) に対する像点距離 (s’, S’,) をそれぞれ求めて、本当に両者の結果が合致するのかを確認しよう、というわけです。
ニュートンの公式の方は、式そのものが極めてシンプルなので、もともと計算に困難はないですが、今回は、敢えてそれを疑って一般的な結像公式 ( 1/s’ – 1/s = 1/f ) を使用して検証してみようというものでした。
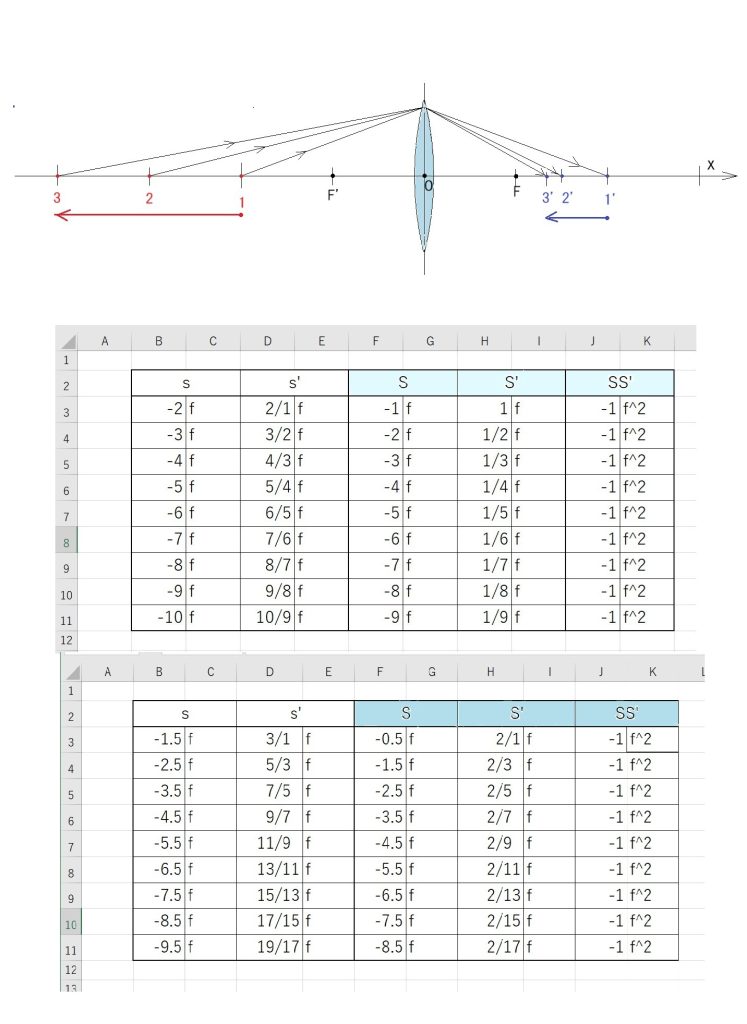
上の表が前回ご紹介した、計算結果で、仮分数出力をしてみたところ、今後は計算がほぼ不要になる法則を発見して狂喜した次第です。(数学が得意な方には、何を今更?と笑われそうですが。)*仮分数
で、実はさきほど作成した下の表は、物点距離を焦点距離の整数倍ではなく、先の表のデータ間の中央を埋めるべく、-0.5f 刻み( s は -1.5f, Sは – 0.5f スタート ) で計算してみた結果の表です。
また、新たな類似の法則が見えて、さらに感激したところです。
s (= n f ) の係数を n と置くと、s’ の係数 n’ = n / (n+1) でした。
ニュートンの公式の場合は、最初からさらにシンプルで、同様に、S (= N f) の係数を N とすると、N N’ = -1 です。(N’ = -1/N ) です。
再三ご説明していますが、一般の公式はレンズ位置基点で物点、像点距離を定義し、ニュートンの公式は、両焦点が基点ですので、
S= s + f ; S’ = s’ – f ; の関係があります。
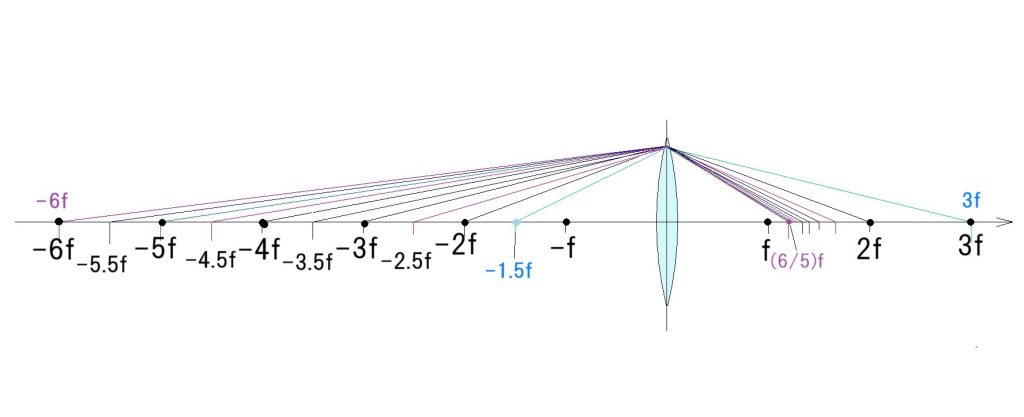
光線が密集していて、全ての光線ペアをマーキングできませんが、出来る限りマークしてみました。
この作図で学べる事ですが;
1.物点が左に向けて -6 f 付近に来ると、像点の左向きの動きが急激に減速し、早くも、さらに物点が左無限遠に行くと、像点が像側焦点に収束する(焦点の定義)ことを予感させますね。
2.逆に、物点が物側焦点に接近すると、像点が急速に右側に逃げて行くことも分かります。物点が物側焦点に来ると、像点は+∞に逃げて行きますが、その傾向がすでに物点 -1.5 f から見え始めていますね。
3.以上から、実物点と実像は、-f ‘ ~f の間には共存できないことも、実感として体感できます。
4.最近発見した、焦点距離を単位とした物点距離と像点距離の数値の法則性から、今回は全く標準的な光路図を作成することも、複雑な計算もすることもなく、製図ソフトを使用して上の画像を作成しました。通常は2本以上の光線の交点を確認するのですが、今回は、先に物点と像点が確定していますので、たった一本の光線で結像が表現できました。