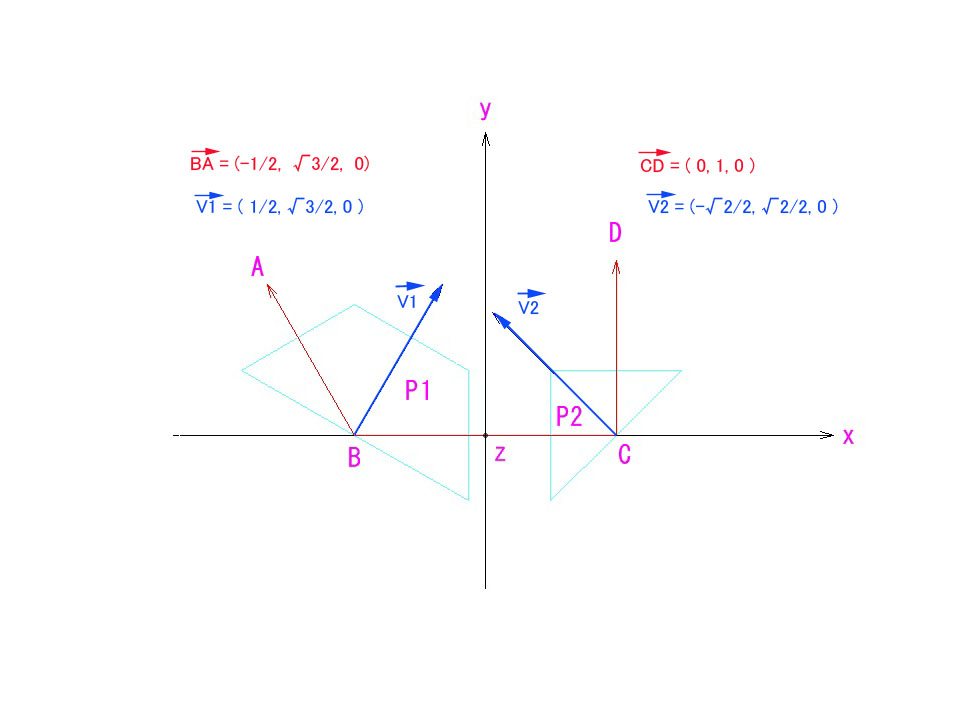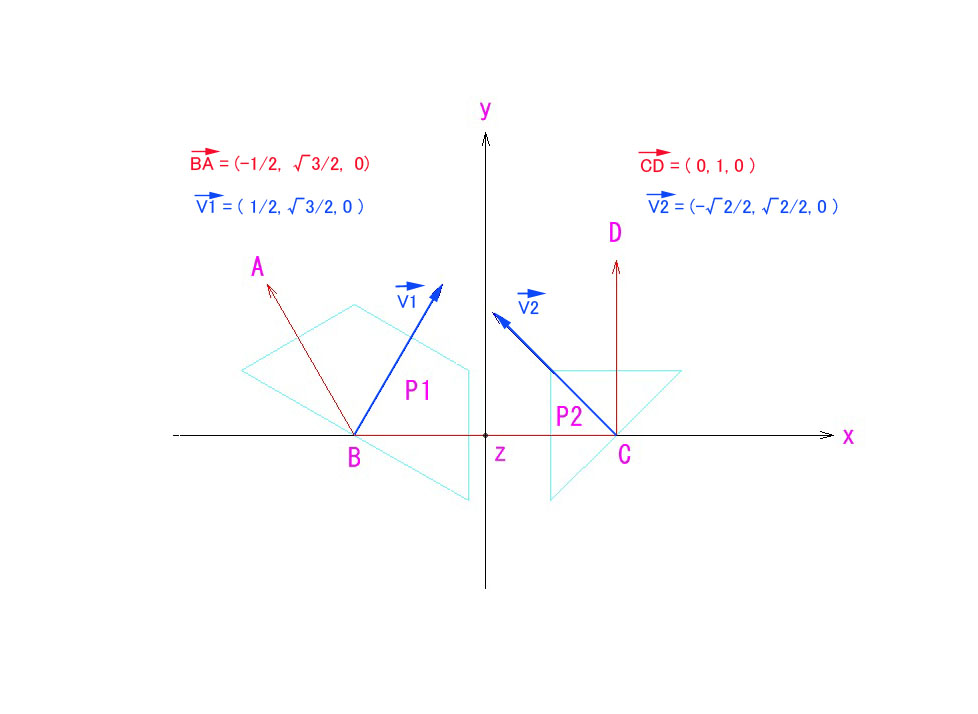
60度転向のプリズム/ミラーを２つ接続して、所定のアングルだけねじると、90度対空の正立ミラーになる、というのがEMSの原理であることは、すでによくご存じと思いますが、その内の１つのプリズムを90度プリズム（直角プリズム）(P2)に交換しても、別の正立解があるのです。
　まず、P2をX軸の回りにθ回転させてみます。→　V2’→
すると、V1→とV2’→が直交するときが正立解なので、直交条件の内積＝0　から、回転させるべきθが求まります。(cosθ＝1/√3）
　次に、求まったθ(cosθとsinθ）から、P2 回転後の (CD)’→が求まるので、(CD)’→とBA→の内積を求めれば、その角度が求まります。(CD)’→とBA→の角度＝αとすると、cosα＝1/2となり、α＝60°、従って、対空角度は180-60=120°、ということが分かります。これは、90度対空よりもさらに30°下を覗き込む角度になります。
(※ V1→、V2→は、反射点、B,Cに於けるそれぞれの法線単位ベクトル。図示したその他のベクトルも全て単位ベクトルとする。）