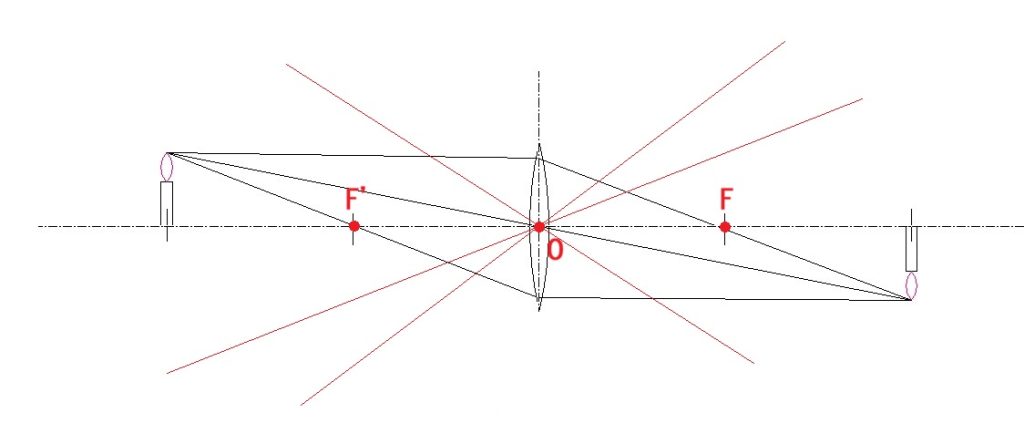
中学理科から見慣れた薄レンズの結像図だと思います。
近軸理論では、薄レンズの厚み＝０と想定しますので、レンズ中心（O）が、全ての基点となり、厚いレンズ系のように、主点の概念を導入する必要はありません。
　中学のおさらいですが、上図のように、
１：レンズ中心を通る光線は全て直進する。（赤線で示した。）
２：焦点を通過する直線は、レンズを出ると、全て光軸と平行に射出する。（光軸と平行に入射する光線は焦点を通る。）
　上記の２点だけ理解できていれば、薄レンズによる結像は全て作図でき、定量的な解析も簡単です。

　では、分厚いレンズや、複数枚で構成された複合レンズ系ではどうだろう？　という話です。
　恐らく、光学黎明期には、上の薄レンズの（O）のような単独の代表点が複合レンズ系の中にないか？、最初は探したに違いありません。　そして、光学台による実験から、そのような好都合な点は存在しないことがすぐに分かったはず。
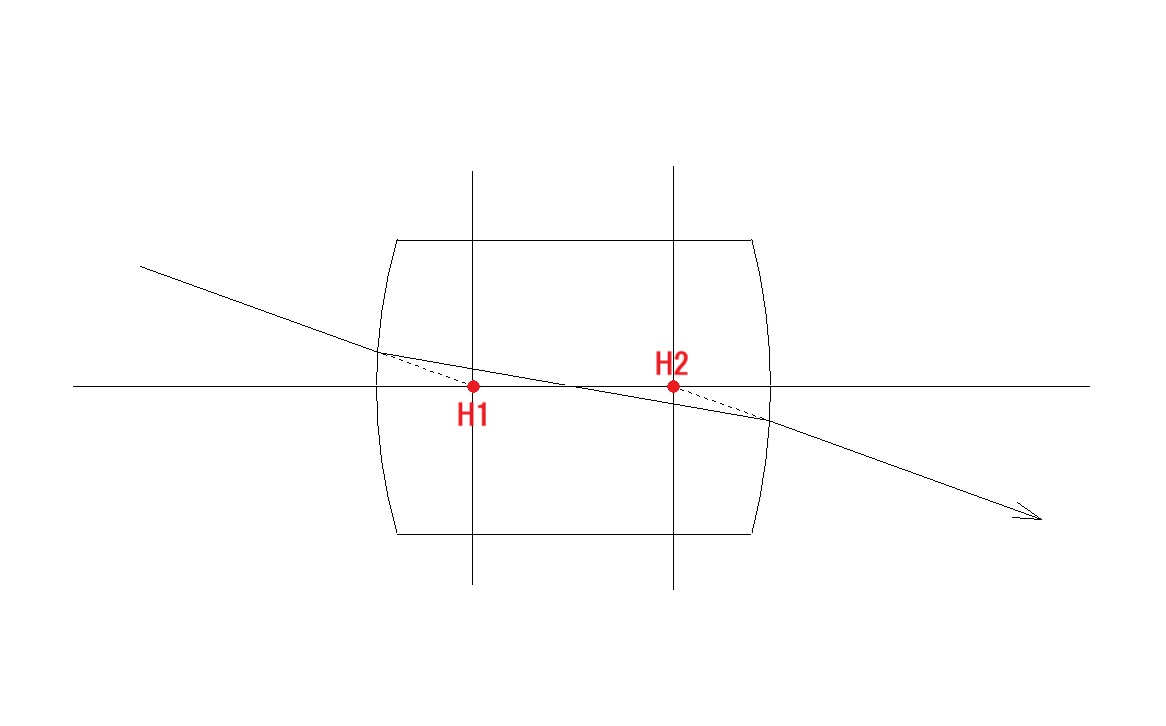
　で、やっと到達した事実が、複合レンズ系では、１点じゃなく、２つの点が、薄レンズの（O）のような”要の点”として存在するということです。次の図を見てください。

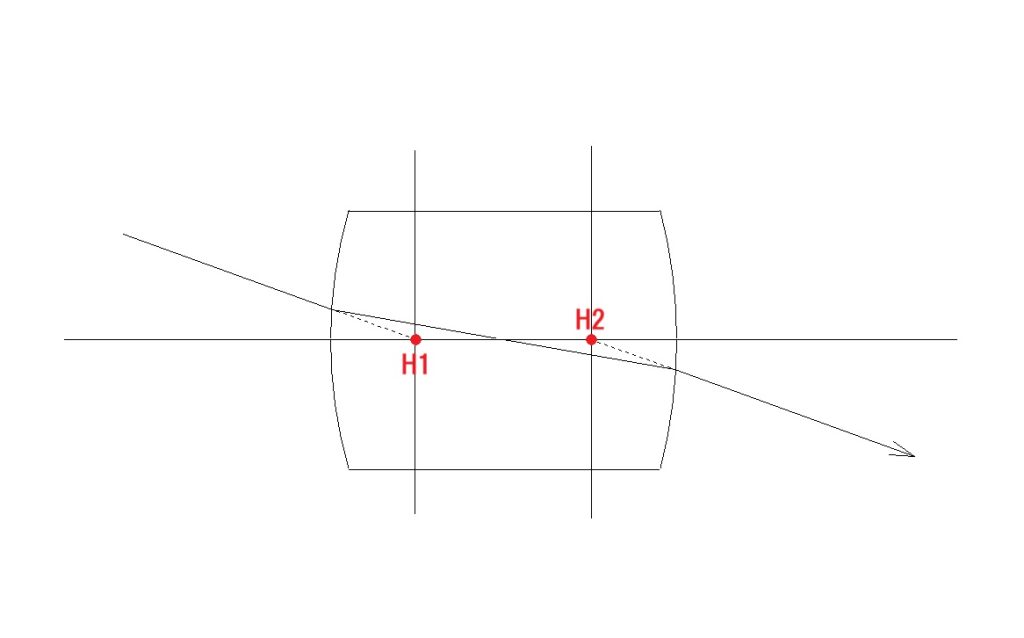
　複合レンズ系には、薄いレンズの（O）のような好都合な単独の代表点は無かったわけですが、食い違いながらも、入射光線と平行に射出して行く光線があることに、光学黎明期の人もすぐに気付いたはず。
　上の図は、厳密には主点ではなく、節点（角倍率＝＋１の共役点）なのですが、物界、像界とも空気の場合は、節点と主点は一致するので、敢えてこの図を示しました。説明がよりシンプルになり、素早く視覚的にご理解いただけると思ったからです。
　この１週間ほど、熱心な天文マニアの方に主点の意味をご説明して来て、あの手この手を考えた結果、到達した ”主点-Tutorial ” です。
　H1に向かう全ての光線が、H2から射出するということ。
（H1,H2は虚物点と虚像点ですから、実際に光線がそこを通るわけではありませんが。）　そして、主点を通り、光軸に垂直な平面が両主面です。
　物側主面の高さ h に入射する光線の全ては、入射角度に関係なく、同じ高さ h の像側主面から射出します。（２つの主面を光学的に定義すると、横倍率=＋１倍の共役面ということになります。 光学で言う、横倍率の横とは、Y軸（縦）方向のことであり、縦倍率というのは、Ｘ軸方向（横方向）のことです。）
　当初はブラックボックスだった複雑な複合レンズ系の骨格を、シンプルに理解するために発見された至宝の点、それが主点であり、節点なのです。
（図は分かりやすく描いていますが、物側主点と像側主点の定義は、その存在位置とは無関係で、像空間に物側主点が来ることや、レンズの外にあることもあります。像側主点も同じ。　従って 物側（第１）主点 と 像側（第２）主点 の並び順が本例とは逆になることもざらにあります。）

　「これでやっと主点の意味が分かった！」と感動してくださった方、ご連絡いただけると、大いに励みになります！ LOL

(主点（節点）とも、一般の光学系は収差のために光線の角度や光軸からの高さによって位置がずれますが、角度も高さも限りなく光軸に近付けた極限値を以って、それらの点を定義します。）