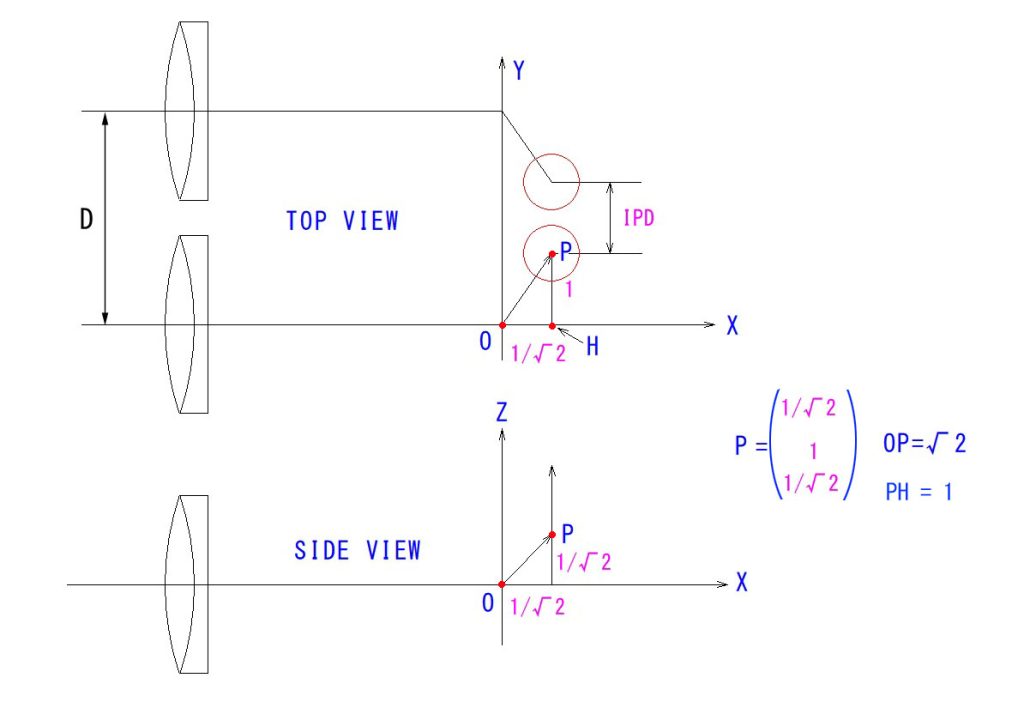
EMSの横シフト量と光路長の関係がよく分かるように可視化しました。
　空間のことについて、2次元で考えていても埒が明きません。
　X-Y-Z 座標で考えましょう。
　OはEMSの第１反射点で、座標軸の原点とします。
PはEMSの第２反射点です。
Pの座標は、( 1/√2, 1 ,1/√2 )となるので、
　OP= √ ( 1/2 + 1 + 1/2) = √2 になります。
　
　つまり、横シフト量を１単位増やすと、光路長は√2増えるということになります。
　　逆に言うと、OPの実長の目幅方向への射影＝OP/√2 ということです。

　ついでに、
OP→とX軸の実角度 θ を求めてみましょう。
OP→ (1/√2, 1 ,1/√2) と X軸方向の単位ベクトル ( 1, 0, 0 ) との
内積＝(1/√2)･1 + 1･0 +(1/√2)･0 ＝1/√2
2つのベクトルの絶対値の積＝√2
cos θ =(1/√2)/√2　＝ 1/2
　　より、 θ =60°　と分かります。