今度は、シンプルな実例で解説します。
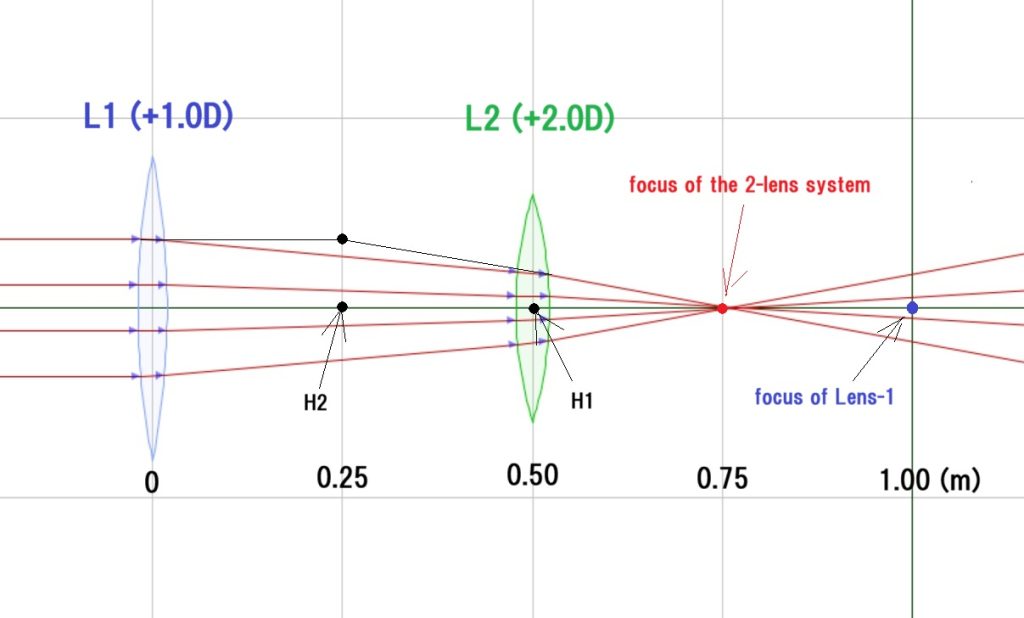
　L1 は、最初に掛ける老眼鏡くらいの度数(+1.0D)の凸レンズです。-Dは、レンズの度数の単位で、”１/焦点距離(m) ”つまり焦点距離の逆数です。
　L2 は、最初の老眼鏡が見辛くなって、2～３回目に更新する度数に近い、+2.0Dの凸レンズです。
（H1は物側主点、H2は像側主点です。両点は、光線の進行方向の並びのこともあれば、本例のように交差していることもあります。）
　図形的に見ても答が出そうな、シンプルな組み合わせですが、最初のサンプルとしては、好適な実例かと思います。
　L1とL2を上図のように配置した時に、２枚レンズ系システムの合成パワー(D)や、各主点の位置がどうなるか？という話です。
　中学校理科（高校物理？）辺りから出て来る、レンズの結像公式( 1/s’ – 1/s = 1/f )を駆使しても答は出ますが、行列（屈折マトリックスと移行マトリックス）を使うと、ずっと計算が楽になりますよ！という話です。

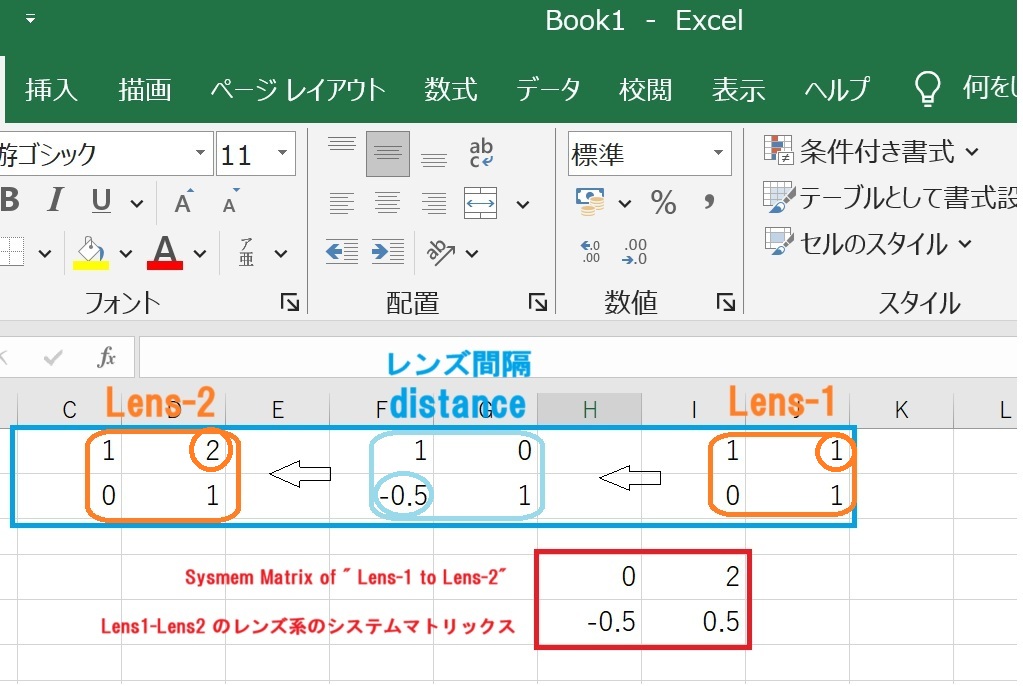
　下の 赤い四角 で囲ったのが、L1～L2 の２枚レンズ系の システム・マトリックス です。上の３つの行列を順に掛け合わせたものです。
　レンズの行列の、朱色の〇 で囲んだ要素が度数で、間隔の行列の水色の〇 が ”間隔×(-1)” です。そこに任意の度数や間隔を代入して掛け合わせれば、全系のシステムマトリックスが得られるわけです。
　レンズの行列は、右上の度数の対角要素は常に０で、他は全て 1 、間隔の行列は、左下の間隔×(-1)の対角要素は常に０で、他は全て 1 、両者とも、行列式の値＝常に 1 です。システムマトリックスも同様。
　前回もご説明した通り、何枚のレンズ、間隔を掛け合わせても、得られるシステムマトリックスの右上の要素には必ず全系のパワー（度数 / D）が来ます。これから主点位置を算出することも出来ますが、今回は割愛しますので、興味がある方は、HPのサイト内検索をしていただくか、直接ご質問ください。
　一度システムマトリックスを求めれば、それが何十枚のレンズで構成されていようが、その後は、システムマトリックスが一枚のレンズと見なせ、想定した物点に対する像点が簡単に算出できるのです。従来の結像公式では、光軸上の位置しか分かりませんが、行列（マトリックス）の方法だと、光軸から任意の高さにある物点に対する像点の高さも同時に得られます。
　２行２列の行列の演算ですから、簡単かと思いますが、エクセルで計算した実例 ↑ をお示しします。MMULT という、行列の積の関数がエクセル内にあります（やり方はネットで検索してください。）ので、行列の演算を忘れた方は利用されると良いです。

( 行列の積は、結合法則は成り立ちます ((AB)C=A(BC)) が、交換法則は成り立たない (ABC≠ACB,CBA) のでご注意ください。また、左から右に掛けていく行列の約束から、行列の並びが光線とは逆の方向になっています。
　これについてご質問があったので、追記(5/27)します。　
実数の場合、”AにBを掛ける”　は　普通 ”A×B ”と表記しますね。（実数の場合はB×A でも結果は同じで実害はないですが）
”行列 (A) に 行列 (B) を掛ける”　は、必ず” (B)(A)”と表記し、計算も、 (B)→(A)　と、左から右に掛ける約束があるのです。
つまり (A)(B) としてしまうと、結果が違ってしまいます。これが、行列の並び順が光の進行方向とは逆になりますよ！という意味です。））