一昨年～去年にかけて連載しました ”松本の光学講座” が不評で、かなりのトラウマを負いましたが、病室で時間がたっぷりあることから、再度の挑戦です。今度こそ、一人でも良いので、「目から鱗が落ちた！」と言わせたい。
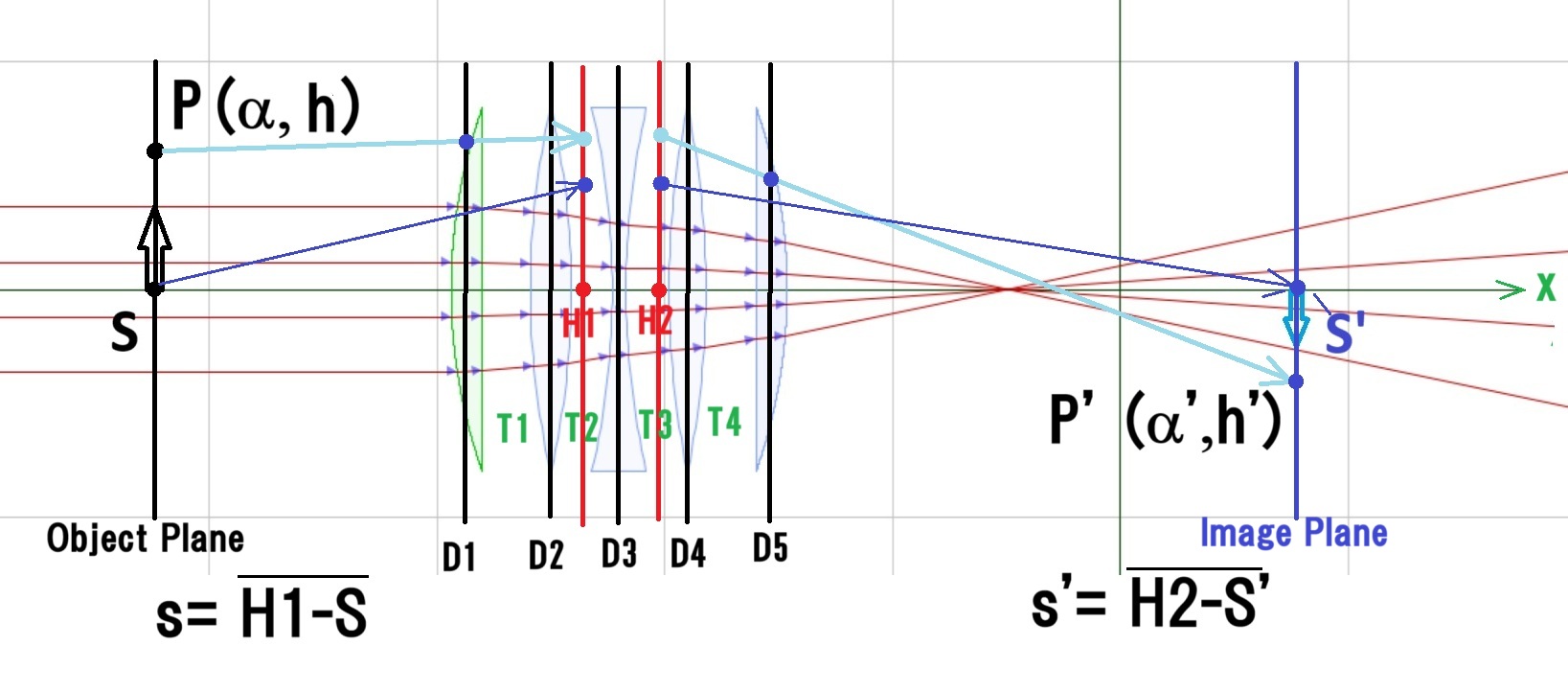
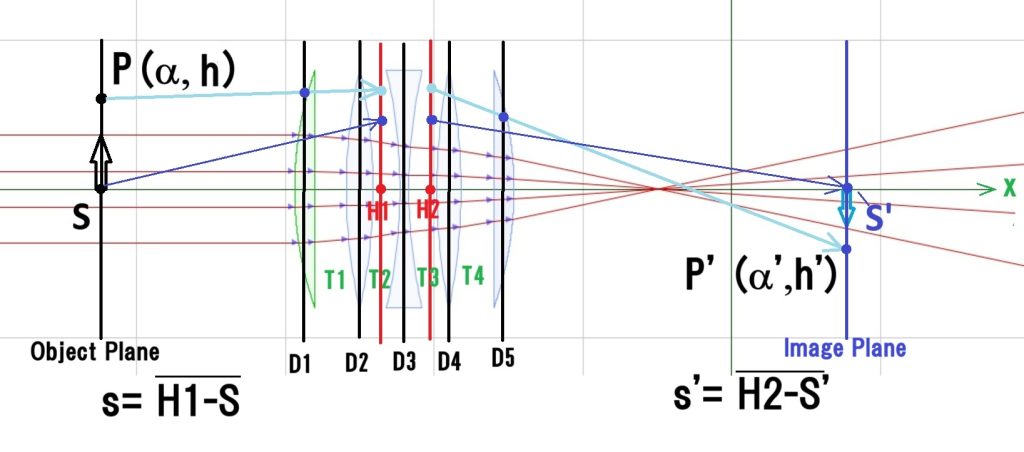
　一般的な 薄レンズの近軸結像公式 の、”1/s’ – 1/s = φ (1/f) ” は良くご存じと思いますが、上図のように、多数のレンズが連なった光学系となると、レンズ1枚ごとに上の公式を当てはめて像点や主点を決定するのは大変な作業になり、現実的ではありません。
　そこで、光軸上の 物点S から 像点S’ を求める、一般的な上記公式ではなく、Meridioal面（光軸とy軸を含む面）の任意の点 P から指定面上の点 P’ が決まる；屈折マトリックスと移行マトリックスの利用 について、前回までの講座でご説明していました。今回は、HPで検索、復習していただきたいところですが、かいつまんで解説させていただきます。

↑ 屈折マトリックス。

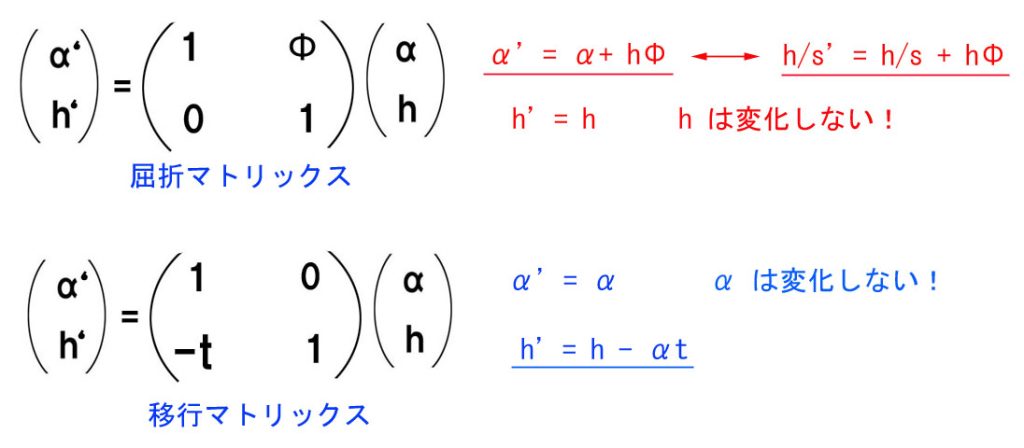
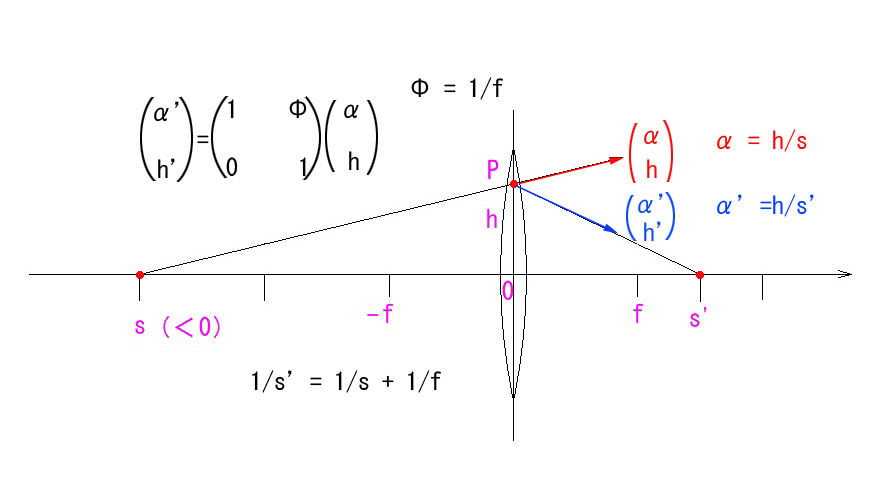
　上が屈折マトリックスです。↑　P を二次元平面ベクトルのように、二元数で表します。ただし、h については x-y 平面の y 座標そのもの（尺度は別です）ですが、α については、x 座標でないことに注意が必要です。
　ｘ座標の席には、α＝tan α で定義された角度が入ります。
　屈折マトリックスでは、P と P’ の二次元平面的な位置が重なります。h = h’ で、α のみが変化するわけです。s’ は直接は求まりませんが、α ‘と h’ から、最後に計算すれば簡単に求まります。

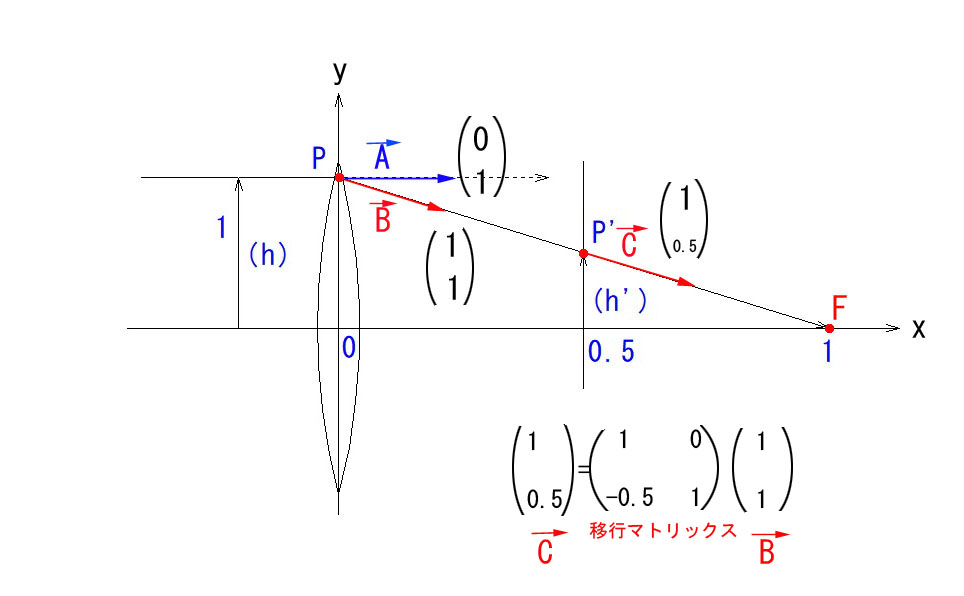
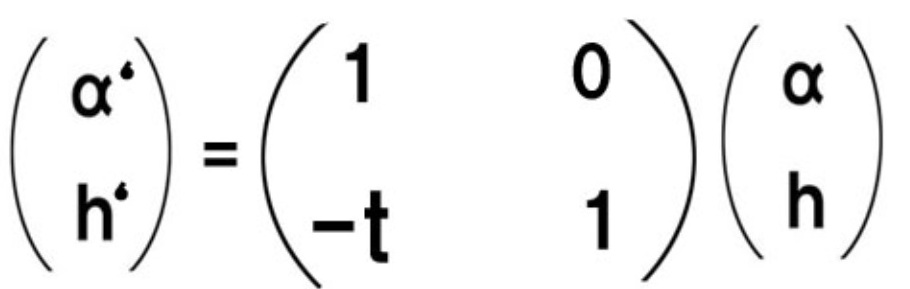
これが移行マトリックスです。
　移行マトリックスは、さきほどの屈折マトリックスとは逆で、α は変化がなく(α’= α )、h のみ変化します。
　以上、屈折マトリックスと移行マトリックスについてご説明しましたが、どちらも行列式が”１”となることにご注目ください。これが、主点位置の決定他、ものすごい効力を発揮します。
　つまり、レンズを任意の間隔で何枚連ねようと、各行列を順に掛けて行って最後に得られる、光学系全体のマトリックスの行列式も”１”になるということです。

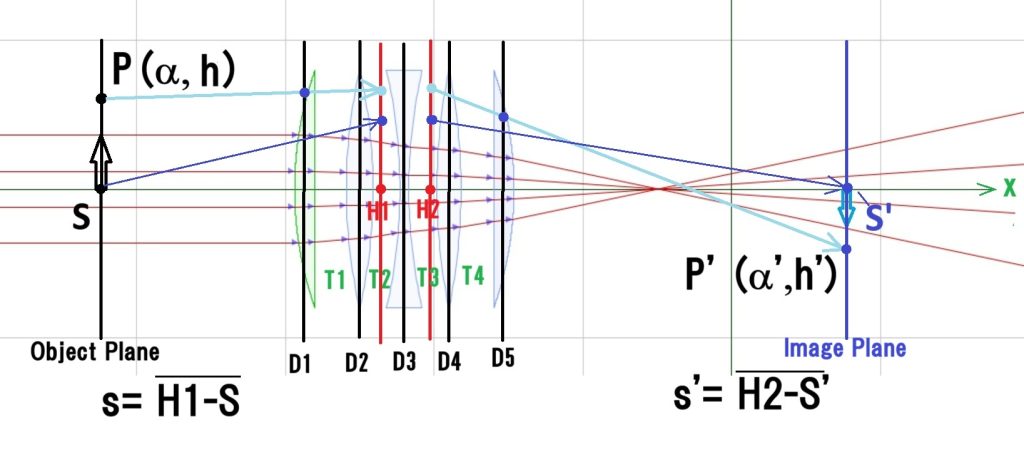
A D
B C　は、S 面（物面）上の任意の点 P ～ S’ 面（像面）上の点 P’ までのシステムマトリックスで、多数の構成要素の行列を掛け合わせた結果として得られるものですが、これを物像マトリックスと言います。マトリックスでもかなりの計算量にはなりますが、上図の理由で、B = 常に０であり、C も常にこの結像系の横倍率であること、さらには、行列式＝常に１であることを知れば、計算は大幅に省けるのです。
　”∵h’=Ch “ は、物像関係だから言えることで、h’/h は横倍率なので、C は常に定数でないとおかしいのです。B に任意の数が発生するとそれが破綻しますから、B = 常に０なんです。
　それから、D=常に光学系の合成パワー(φ＝1/f) となっていることも忘れてはいけません。どんなに長く要素を連ねた光学系であっても、システムマトリックスの右上の要素が常に合成系のパワーだなんて、興奮しませんか？

　D1～D5までの構成要素の行列を積算すると、この光学系全体のシステムマトリックスが算出できますが、それからさらに基点が S 面と S’ 面になるように両サイドに移行マトリックスを掛けると、SーS’ 面間のシステムマトリックスが求まり。Ｓ面上の任意（Meridional面限定）の点 P が S’ 面のどこに達するかが分かるわけです。
　恐らく、初心の方は、近軸前提の理論なのに、光軸からの高さを扱うのは矛盾していないか？と思われるはずです（私もそうでした。）が、高さは相対的な意義がある（図のスケールを真に受ける必要はなく、単位はmmだろうと、ミクロンだろうと関係ない）し、無収差の光学系と仮定すれば良いわけで、主点や結像点の位置のみならず、光学系の絞りの位置や口径を考察するのに、この二元数表記が奏功するわけです。　光学系の設計の最初のたたき台としての”骨格”を決定するための、極めて有効で利用価値の高いツールなのです。

　蛇足ですが、「厚みが無視できるレンズにしか役に立たない理論じゃないのか？」というご質問に先回りしてご説明します。　レンズの厚みが無視できない場合（普通はそうですよね！）は、レンズの前面と後面を限りなく薄く削いだ片平レンズと想定し、２枚の薄レンズの間に平行ガラス板を挟んだ物と想定すれば良いのです。中間の平行ガラス板の厚みは、1/N（屈折率）の距離の空気層と等価なので、換算距離を用いれば、理想の薄レンズの集合体と見なせるわけです。