以前の”EMSの種明かし”が理解できない、と言う方が多いので、
今回は全く切り口を変えてご説明します。

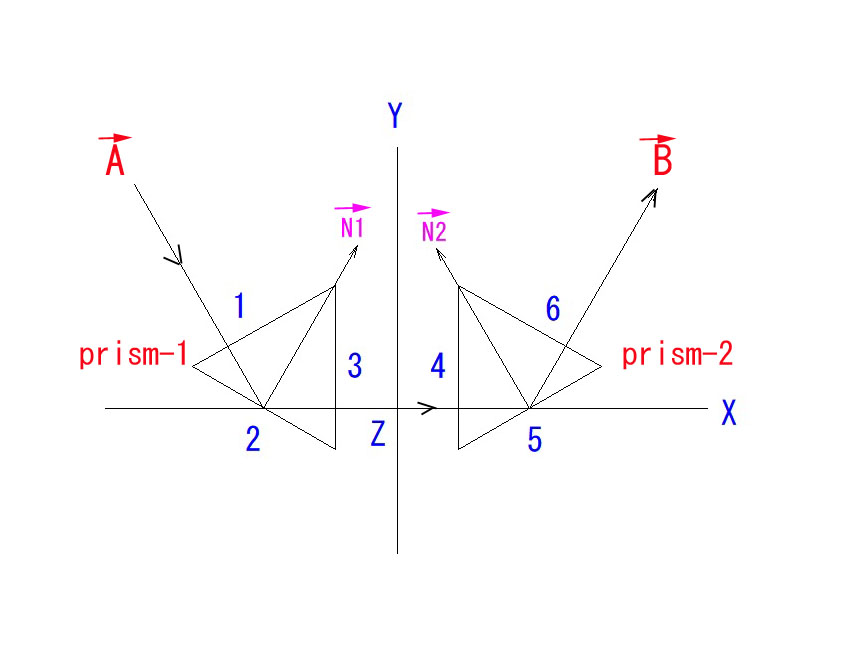
　まず、上図のように、正三角（実際は台形になりますが）プリズム2個を対面させて、プリズム2をＸ軸の回りに一定角回転させると、正立プリズムになるということ、これを既成事実として受け入れてください。
　次に、どのくらいねじると、正立解になるのかご説明します。
　これも、専門的に追及すると、スキップされると思うので、２つのプリズムの反射面（２と5）の法線が
直交する時が正立解になることも、アミチプリズムの既成事実として受け入れてください。

　上記の前提で、話を進めます。

　主光線ベクトルAは第１プリズムの反射点２→第2プリズムの反射点5を経てベクトルBとなります。

2つの反射点での法線ベクトルをそれぞれ、ベクトルN1,ベクトルN2とします。

ベクトルN1は、
|　1|
| √3|
|　0|　　と表せます。

ベクトルN2は、
| -1|
| √3|
|　0|　　と表せます。

プリズム2をθだけX軸の回りに回転させた時が正立解で、その時、ベクトルN1とN2が直交、
即ち、→N1と→N2の内積＝0　になれば良いので、式を立てます。

| 1 　 　 0 　 　 0 | 　 |　-1| 　　 　 |　　-1　 |
| 0 　 cosθ 　-sinθ | 　 | √3| 　= 　 | 　√3cosθ|
| 0 　 sinθ 　 cosθ | 　 |　 0| 　　 　 | 　√3sinθ|

上の式の右辺が、プリズム2の回転後のベクトルN2’です。

| 1| 　　 　 | 　 -1 |
|√3| 　 . 　 |√3cosθ| 　= 　 0　
| 0| 　　 　 |√3sinθ|

↑ベクトルN1とN2’の内積＝0　ということ。

展開すると、

-1+3cosθ=0

cosθ= 1/3

いかがでしょう？　同様の方法で、ベクトルAと、プリズム2の回転後のベクトルB’が直交していることも分かります。