先日の、ニュートンの公式の検証についての講座が友人に不評で、原因を探っているところですが、前提のご説明が不十分だったのでは？と思い、少し、仕切り直しです。
　いきなり整然とした計算結果表を見せ付けられても、威圧にしか取れない方もあったのかも知れません。
　そこで、ほぼ計算前の表をお示しし、何をやろうとしていたのか？ということをまずは共有させていたくのが先決だと気付きました。
　そして、結果として、（今後は）計算不要な法則が見つかった感激を、少しでも皆様とシェアさせていただけたら、大変励みになります。

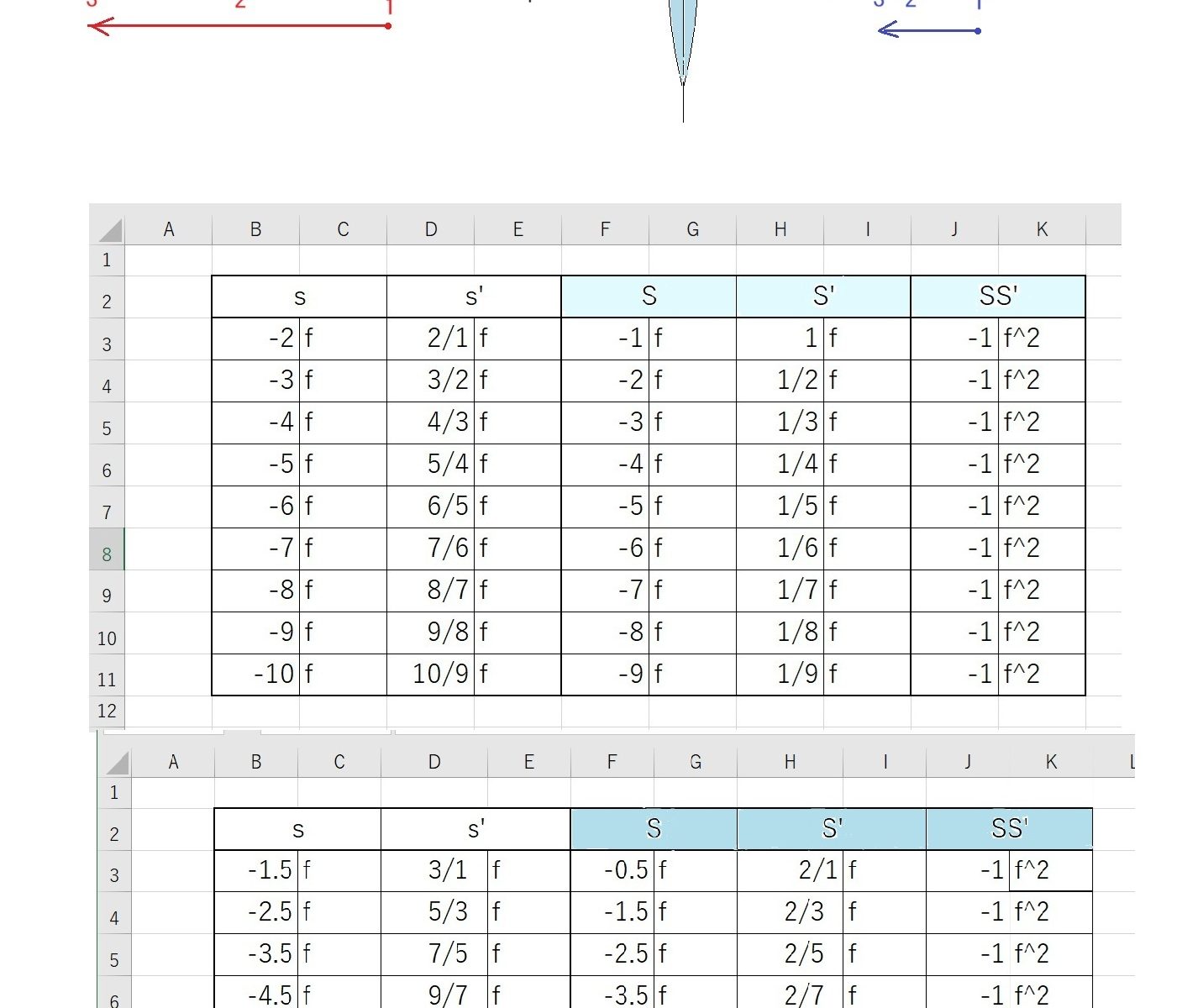
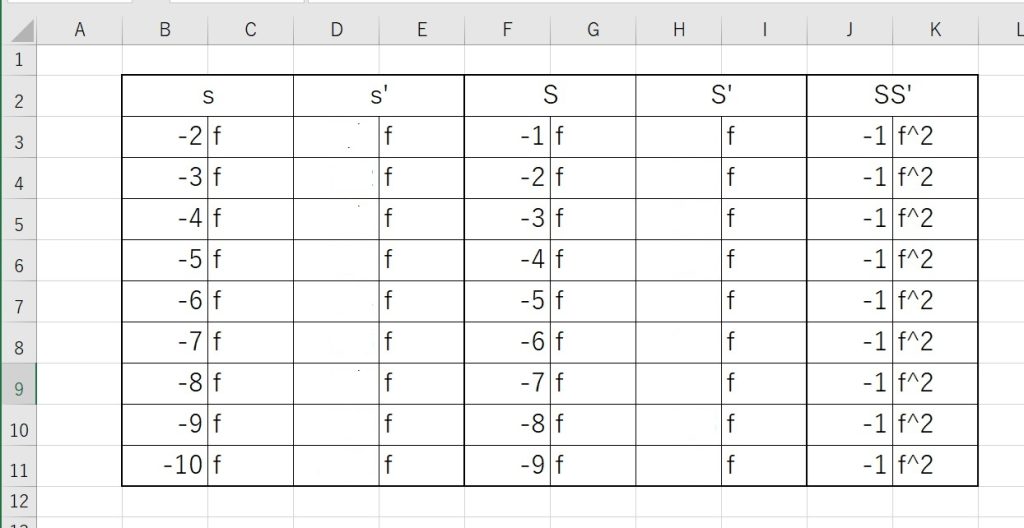
　上の表は、これから何を求めるか？の最初の前提です。レンズの焦点距離＝ f に於いて、任意の物点距離 (s, S,) に対する像点距離 (s’, S’,) をそれぞれ求めて、本当に両者の結果が合致するのかを確認しよう、というわけです。
　ニュートンの公式の方は、式そのものが極めてシンプルなので、もともと計算に困難はないですが、今回は、敢えてそれを疑って一般的な結像公式 ( 1/s’ – 1/s = 1/f ) を使用して検証してみようというものでした。

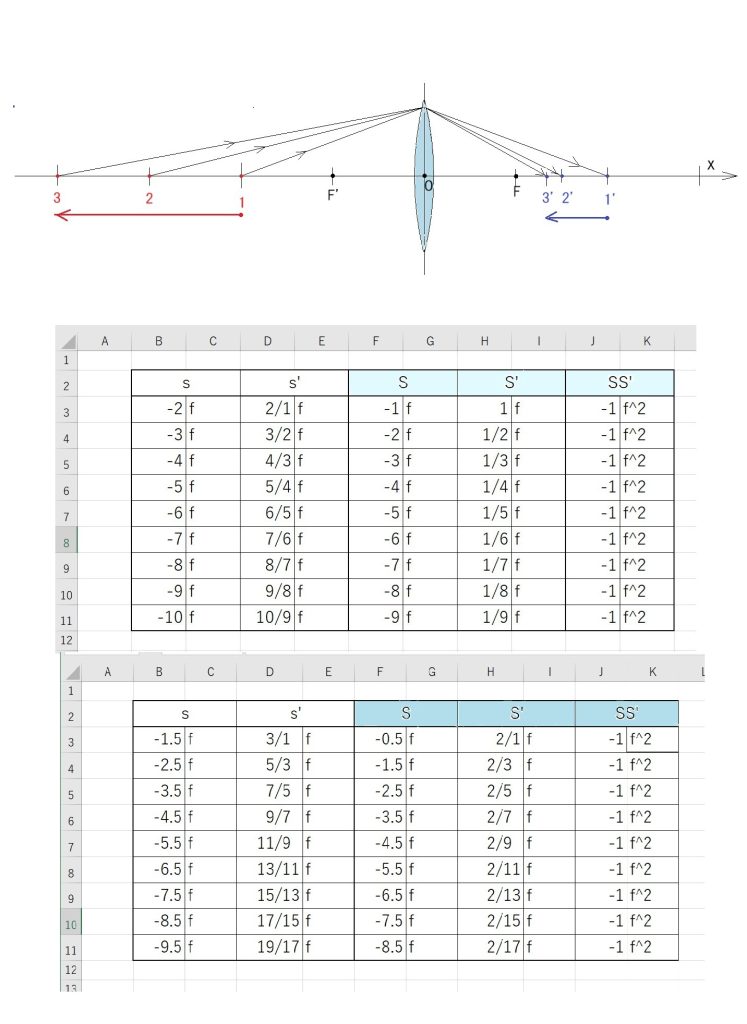
　上の表が前回ご紹介した、計算結果で、仮分数出力をしてみたところ、今後は計算がほぼ不要になる法則を発見して狂喜した次第です。（数学が得意な方には、何を今更？と笑われそうですが。）＊仮分数
　で、実はさきほど作成した下の表は、物点距離を焦点距離の整数倍ではなく、先の表のデータ間の中央を埋めるべく、-0.5f 刻み（ s は -1.5f, Sは – 0.5f スタート ) で計算してみた結果の表です。
　また、新たな類似の法則が見えて、さらに感激したところです。
s （= n f ) の係数を n と置くと、s’ の係数 n’ ＝ n / (n+1) でした。
ニュートンの公式の場合は、最初からさらにシンプルで、同様に、S (= N f) の係数を N とすると、N N’ = -1 です。(N’ = -1/N ) です。
　再三ご説明していますが、一般の公式はレンズ位置基点で物点、像点距離を定義し、ニュートンの公式は、両焦点が基点ですので、
S= s + f ； S’ = s’ – f ; の関係があります。

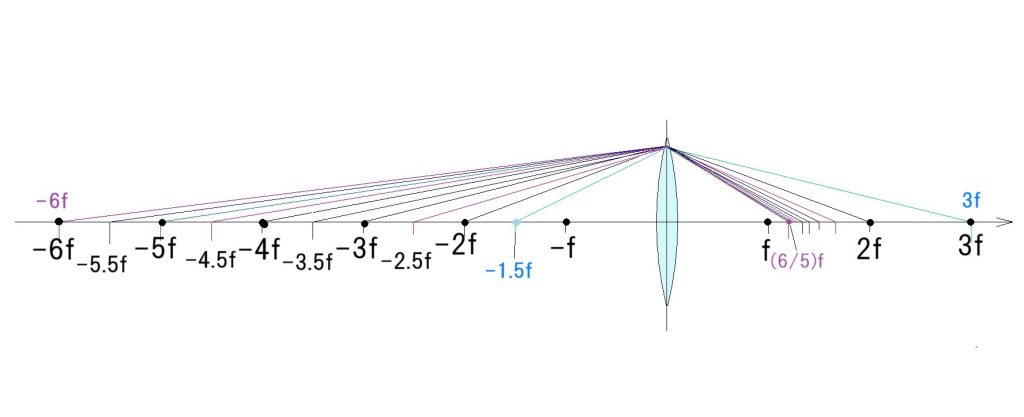
　光線が密集していて、全ての光線ペアをマーキングできませんが、出来る限りマークしてみました。

　この作図で学べる事ですが；

１．物点が左に向けて -6 f 付近に来ると、像点の左向きの動きが急激に減速し、早くも、さらに物点が左無限遠に行くと、像点が像側焦点に収束する（焦点の定義）ことを予感させますね。

２．逆に、物点が物側焦点に接近すると、像点が急速に右側に逃げて行くことも分かります。物点が物側焦点に来ると、像点は＋∞に逃げて行きますが、その傾向がすでに物点 -1.5 f から見え始めていますね。

３．以上から、実物点と実像は、-f ‘ ～f の間には共存できないことも、実感として体感できます。

４．最近発見した、焦点距離を単位とした物点距離と像点距離の数値の法則性から、今回は全く標準的な光路図を作成することも、複雑な計算もすることもなく、製図ソフトを使用して上の画像を作成しました。通常は２本以上の光線の交点を確認するのですが、今回は、先に物点と像点が確定していますので、たった一本の光線で結像が表現できました。