The amazing vitality of YAMABUKI (Japanese Rose)/ 山吹 の生命力!

It is the photo sent by my wife on the LINE with the message below.
Tatsuro ! Here is the News, which will surely cheer you up!
This is the YAMABUKI (Japanese Rose) which I picked up at the mountain last spring.
After firstly enjoying it in the vase for a while, I planted it in a flower pot.
But the twig was sadly broken under the weight of the snow, and I had connected it by the scotch tape as a first aid, with a faint hope of surviving.
Now, I found the BUD just before blooming!
Amazing vitality of the PLANT !
たっちゃん に元気をプレゼント。去年山で取ってきた山吹の花。花瓶に挿していたら、根が出たので土に刺した。
雪で枝が折れたところをセロテープで補修、ダメだと思っていたのに、蕾をつけ花を見せてくれました。強いでしょ。
(離れにいた妻からのラインメッセージ)
Another EMS-UL SET for Korea completed !
松本の光学講座 2024;復習5/Basic theory-6/ 超基礎からの復習- 6/ 3次元座標/久しぶりのクイズ!
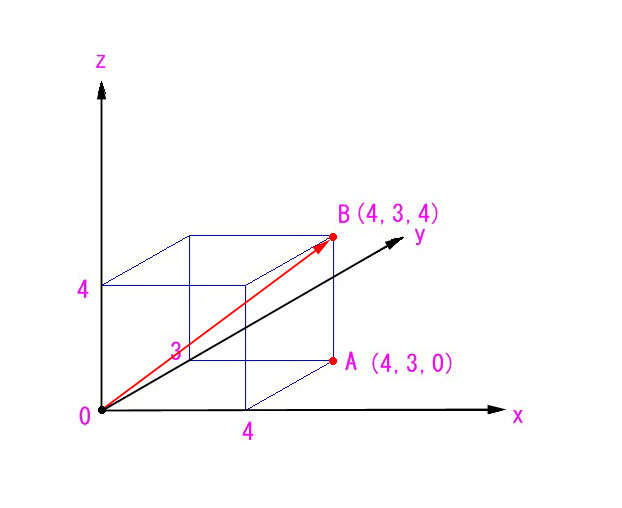
Q1:The length of OA?(OAの長さ?)
Q2 : The length of OB?(OBの長さ?)
角度関係も簡単に求まりますが、今回はここまで。
解答と解説(3/30追記)
解答
Q1 —– 5
Q2—— √41 (SQR41)
X-Y座標(x,y)では、原点からの距離=√(x^2+y^2) となります。
X-Y-Z座標(x,y,z)では、原点からの距離=√(x^2+y^2+z^2) となります。
X-Y-Z座標の A(ax, ay, az), B(bx, by, bz) 2点間の距離は、
√{(ax-bx)^2 + (ay-by)^2+(az-bz)^2} となります。
辺長の比が 3 : 4 : 5 の三角形が、斜辺を5とする直角三角形になることは有名です。
3^2 + 4^2 = 5^2 ですからね。^^(三平方(ピタゴラス)の定理)
さらに、ベクトルの内積を見れば、2つのベクトル間の角度(cosθ)も分かります。
松本の光学講座 2024;復習5/Basic theory-5/ 超基礎からの復習- 5-反射の法則と屈折の法則の代数的検討
代数的考察には踏み込まない、と一旦申しましたが、シンプルな方法が閃いたので発表させていただきます。
まずは、反射の法則から・・・。
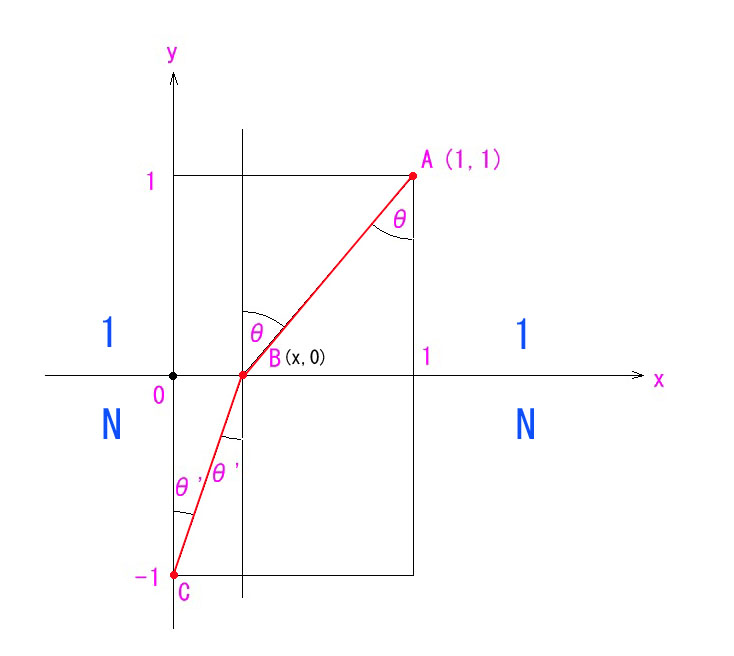
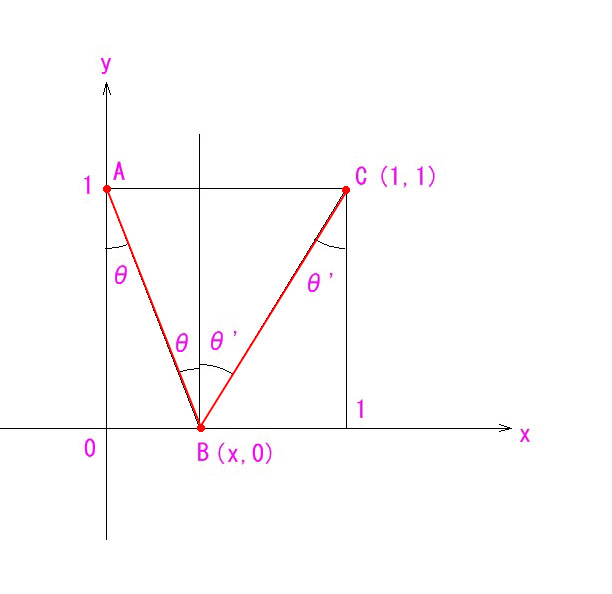
通常は、AB = √(x^2+1) , BC = √{(1-x)^2+1}から、f(x)=√(x^2+1)+√{(1-x)^2+1}を微分して法則を導き出すのですが、証明したい法則は θ = θ‘ なので、最初から三角関数を用いた方がシンプルになります。
AB + BC = 1/cosθ + 1/cosθ‘ —– f(θ)
と、総光路長が非常にシンプルに表せられます。
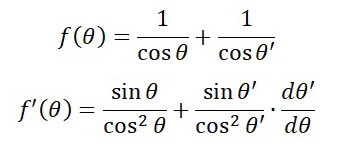
θ で微分すると、上記のようになります。
dθ’/dθ が邪魔物ですね。
そこで、もう一つの関係式、tanθ + tanθ’ = 1 の両辺を微分してみます。
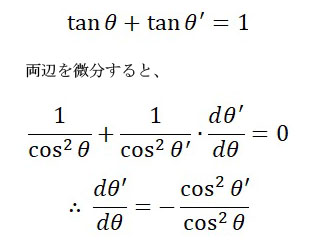
これで、最初の f'(θ) の式から、dθ’/dθ を消去できます。
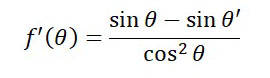
厳密には、これをさらに微分するのですが、今回は割愛して、0<x<1 の間に解が一つある前提で進めます。
f'(θ) = 0 のときに、f(θ) が最小値になるので、
sinθ = sinθ’ 、すなわち、θ = θ’ が導けました。
屈折の法則も、同様の方法で導けます。
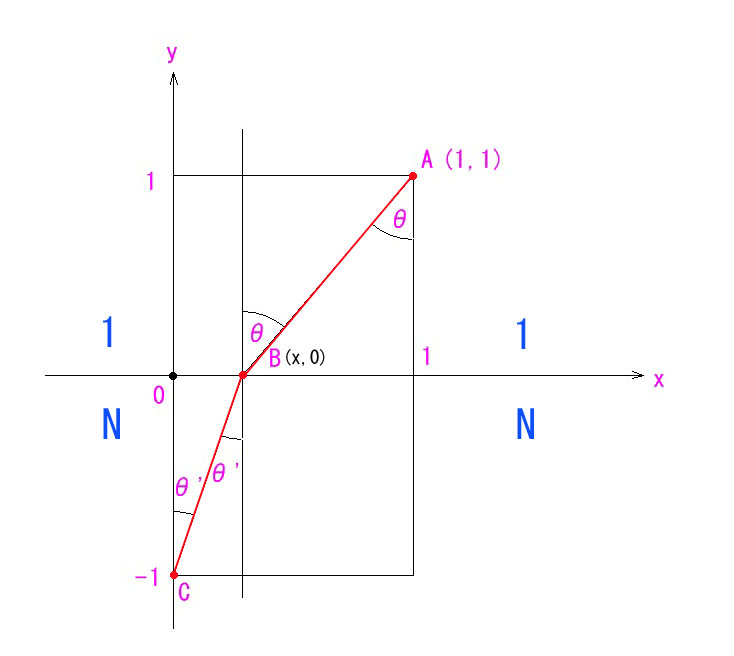
反射の例との違いは、Y 軸の負領域と正領域で屈折率が違うということです。
上図では、Y 軸の正領域は空気中で屈折率1,負領域の屈折率をNとしています。
光の速度は屈折率に反比例するので、同じ距離でも、Y軸の負領域では、時間がN倍かかるわけです。
Y軸の正領域の速度がN倍、と考えても同じことです。
従って、最小所要時間の経路を求めるには、Y軸の負領域の光線の長さを最初からN倍して考察することになります。
AB + BC = 1/cosθ + N/cosθ‘ —– f(θ)
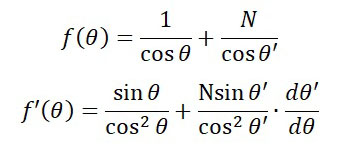
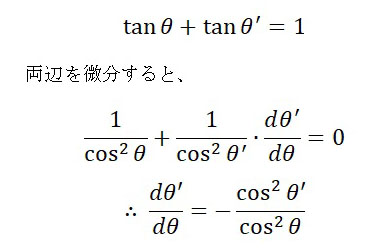
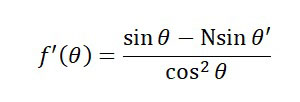
先程と同様に、f'(θ) = 0 のときに、f(θ) が最小値になるので、
sinθ = Nsinθ’ が導けました。
いかがでしょう? 反射と屈折で数式がほとんど同じですね。
以上から、反射面は光線の向きが反転することも考慮して、屈折率=”-1″の特殊な屈折面として、通常のレンズの追跡方法に一般化出来ることが分かりましたね。
松本の光学講座 2024;復習5/Basic theory-4/ 超基礎からの復習-4 反射の法則
前回の屈折の法則、分かりやすく工夫したつもりでしたが、分かりにくかったでしょうか?
反射の法則の方がずっと明快なので、先にこちらをUPすべきだったかも分かりません。
今度こそ、すぐに逃げないで最後までお付き合いください。
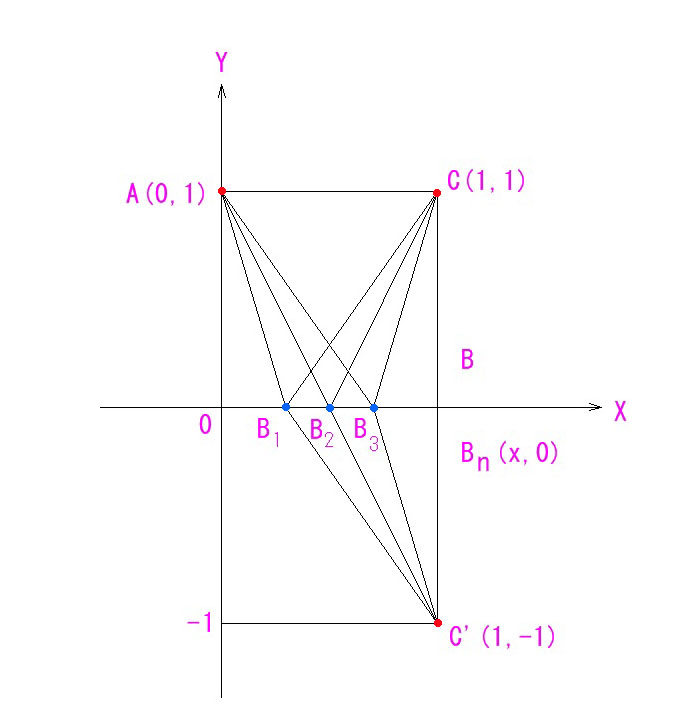
あなたの居る位置を A(0,1) とし、C に最短路で移動したいとします。
それは簡単で、直線 AC に添って進めば良いですね。
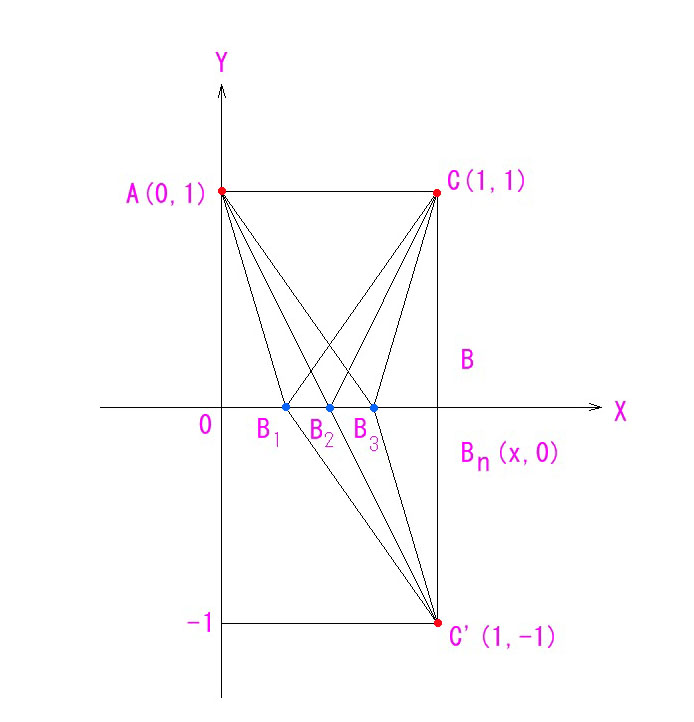
ここで、条件を付けます。Cに行く前に、X軸で代表される壁を一度タッチしてからCに行かないといけないとします。その最短路を考えてみましょう。
X軸の壁にタッチする位置 Bn (x, 0) は、0<x<1 の範囲で候補は無数にあるわけですが、その距離を考える前に、C の、X軸に対して対称な点 C’を作図しておきます。
すると、Bn C = Bn C’ となることが図から明らかです。
ということは、総経路長=ABn + Bn C = ABn + Bn C’ より、
ABn + Bn C’の最短路が 総経路 A-Bn-C の最短路となり、
直線AC’がX軸と交わる点B2 が最短路となるタッチポイントと言えるわけです。
このように、光線は常に最小所要時間の経路を進むことが分かっています。
作図に当たって、A,Cに具体的な座標を与える必要はなかったのですが、代数的に検証してみたい方のために、敢えて数値を与えました。
Another EMS-UL SET for Korea in the making
松本の光学講座 2024;復習5/Basic theory-3/ 超基礎からの復習-3 屈折の法則
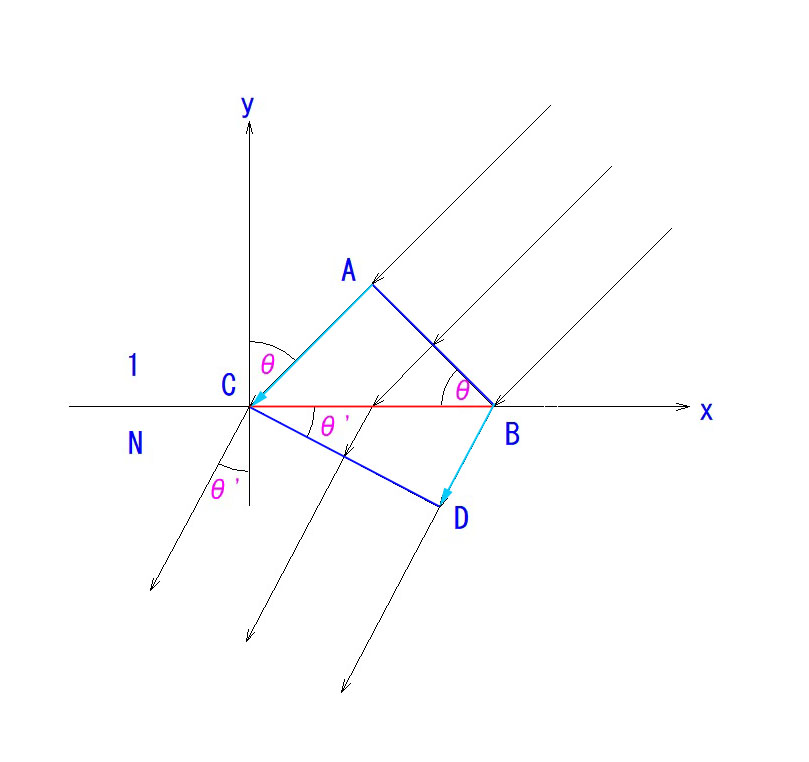
光が最小所要時間の経路を通ることから、所要時間の関数を立てて微分することで、純粋に代数的に屈折の法則を導入できますが、数式を敬遠される傾向が分かったので、今回は純粋に幾何学的、視覚的に納得いただけるモデルを作りました。
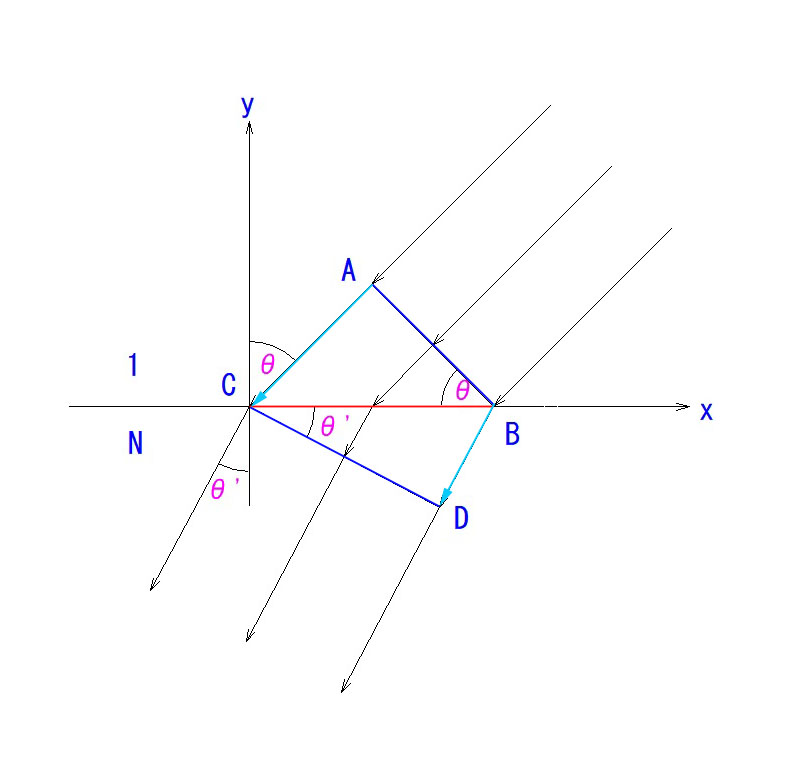
光が光学的密度(屈折率)が異なる界面で屈折する事実—-①、また、平面波(無限遠からの平行光線)の波面(光線に垂直な面)は、屈折前後で崩れない—-② ことも前提として受け入れてください。
さらに、光の進行速度が屈折率に反比例する事実。—③ も認めてください。
つまり、AC間の光の進行速度は、BD間の N 倍になるということです。
波面ABがCDに至る時、ACを移動する時間とBDを移動する時間が同じでないと、上の前提が崩れます。
これより、
sinθ = Nsinθ‘ が確定するわけです。(∵ AC = N・BD)
( x軸より上が空気の例ですが、両サイドともガラス等(/ 液体)であれば、
Nsinθ = N’sinθ‘ )
*BC=1 と置くと分かりやすいです。
EMS-UL SET for Korea completed !
松本の光学講座 2024;復習5/Basic theory-2/ 超基礎からの復習-2
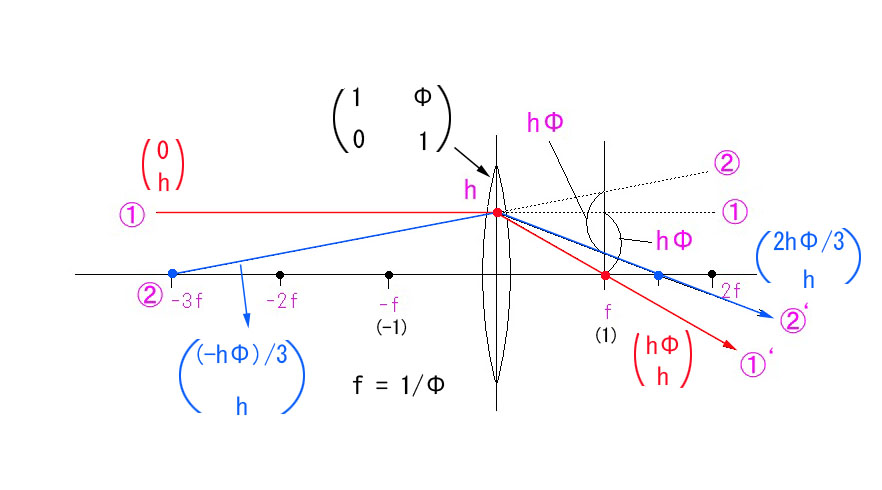
近軸領域では、光線がレンズで屈折するときの屈折角度は、レンズに入射する光線の高さ h とΦに比例します。入射光線の元の傾斜角度を α とすると、屈折後の傾斜角度(←定義された角度)α’ = α+hΦ となります。
つまり、レンズを通過する都度、傾斜角度が+hΦずつ加算される、ということです。Φ>0であれば、左から右に進む光線は、下向きの角度 hΦ ずつ曲がる、ということです。
赤い光線も、青い光線も、同じ角度だけ曲がる、ということになります。
もともと、近軸という特殊な条件で、” h/距離 ” で定義された傾斜角度 α なので、h/α から距離が逆算できるわけです。
入射光線②のような傾き α<0 とし、①のように光軸に平行な入射光線の傾き α =0 とします。
また、屈折光線①’や②’のように下向きに傾いた α >0 とします。
距離の正負の定義から、自ずと傾斜角の正負も決まります。
今一度、整理しますと・・、
*複数のレンズを密着して重ねた場合、合成度数は、単純に各々のレンズのΦ(度数)を合計したものになります。
レンズに間隔がある場合は、
平行光線が最初のレンズに到達する高さ=1として、その光線が各レンズを通過する高さとそのレンズのΦを掛けたものを、繰り返しレンズ枚数だけ加算したものが合成度数になるわけです。
どちらのケースも、ほぼ単純な足し算に帰結するわけです。2行2列の行列が利用できる所以です。