「さっぱり分からん！」という言葉に潜む傲慢さに気付いて欲しい。
それが、分かろうと努力する動機につながるのであれば、傲慢とは逆なんだけど、その裏には、「自分は長年この分野にかかわって来たから、最低限のことは理解しているが、説明がまずいから理解できない。」とか、「そんなことは知らなくても、何の不利益もない。知る必要もない。」と思っている方が結構おられる気がする。
　”焦点”とか、”F値”とか、”入射角”とか、もはや空気のようになっている基礎的部分で誤解しているから先に進めない！ということに早く気付く方は幸いだ。しかし、業者さんや、古参マニアになるほど、基礎的な用語への信念は頑なで、決して疑問に思われることがない。
　「大きなお世話だ！」とお怒りの言葉が聞こえる気がするけど、この仕事を35年続けて来て、引退を数年後に控えた今、何としてもそこに一石を投じたくて仕方がなくなったわけです。それは、社会貢献というよりも、価値観を共有できる人を少しでも増やしたいという、自分の欲求が優っているかも知れませんが。

　今日は、基礎光学の前提とも言うべき、”入射角”について取り上げました。
誤解している方があまりにも多いからです。

図の 1-2, 2-3, 3-4 は、全て同じ長さです。
　1-2-3-4 の光路は、水色の立方体を3個連ねた四角柱の角の 1 から、上の面の対角の 4 に至ります。
　その経路は、他の3面を最短路で辿っています。（3面を展開すると直線になる。）

これをコの字状に折り曲げれば、上の斜視図の状態になります。

　皆さんに宿題があります。
上の方の図をプリントアウトしていただき、右眼仕様の光線を違う色で追記してみてください。
　また、各反射点に於ける面法線も追記してみてください。それが出来たら、EMS内の光路が大分理解できたことになります。

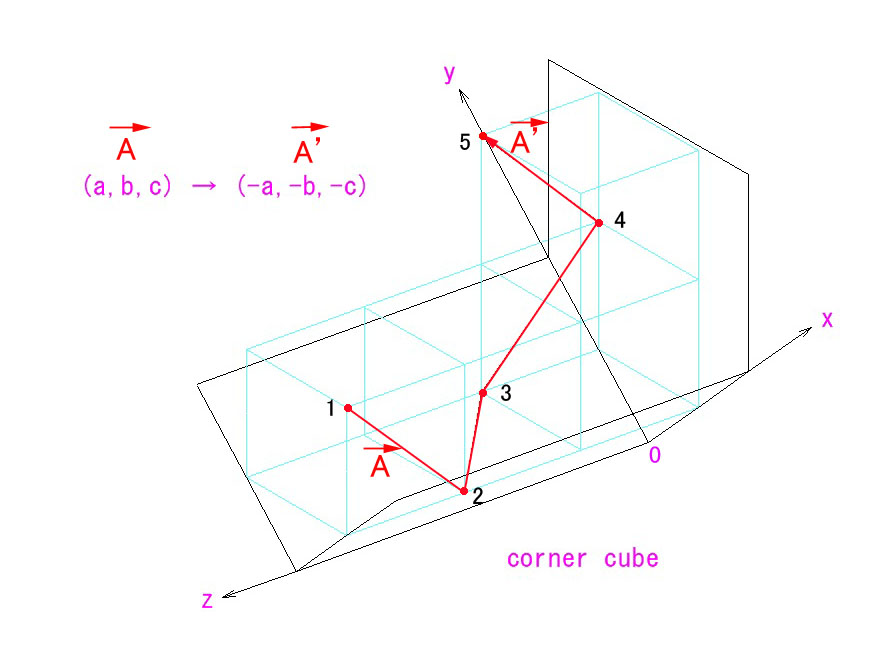
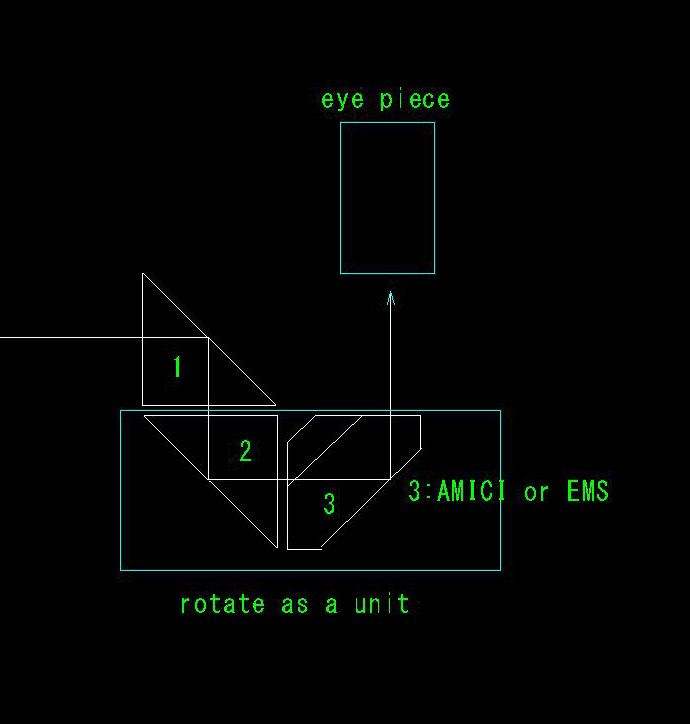
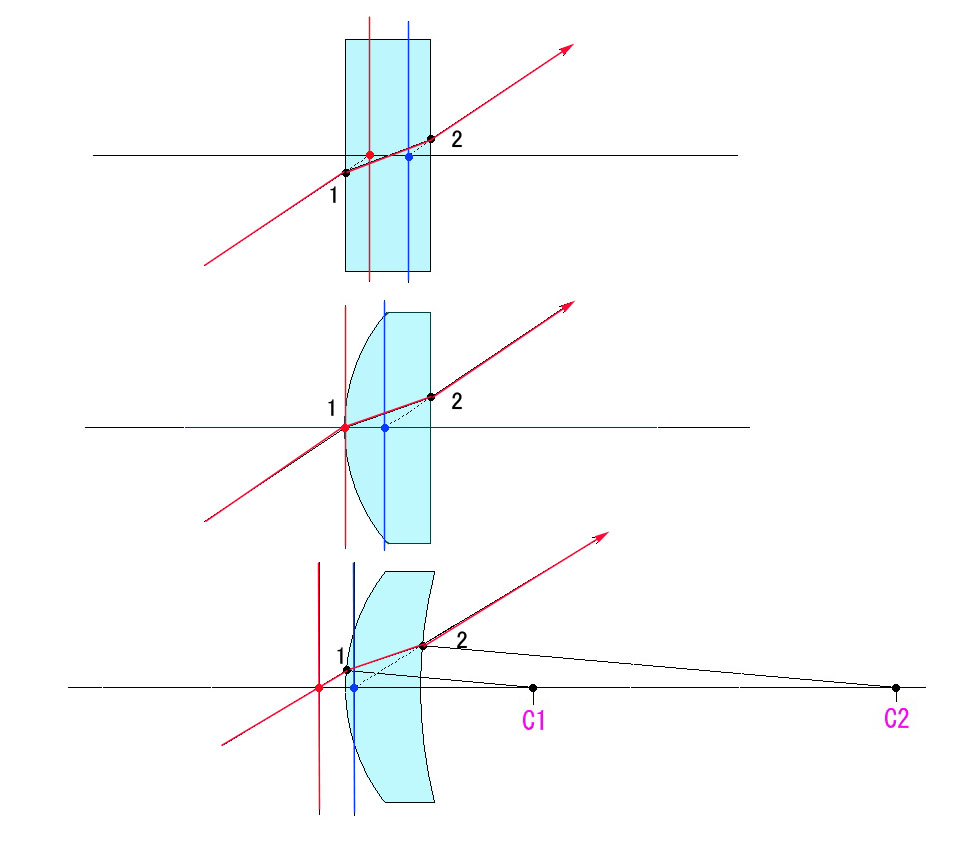
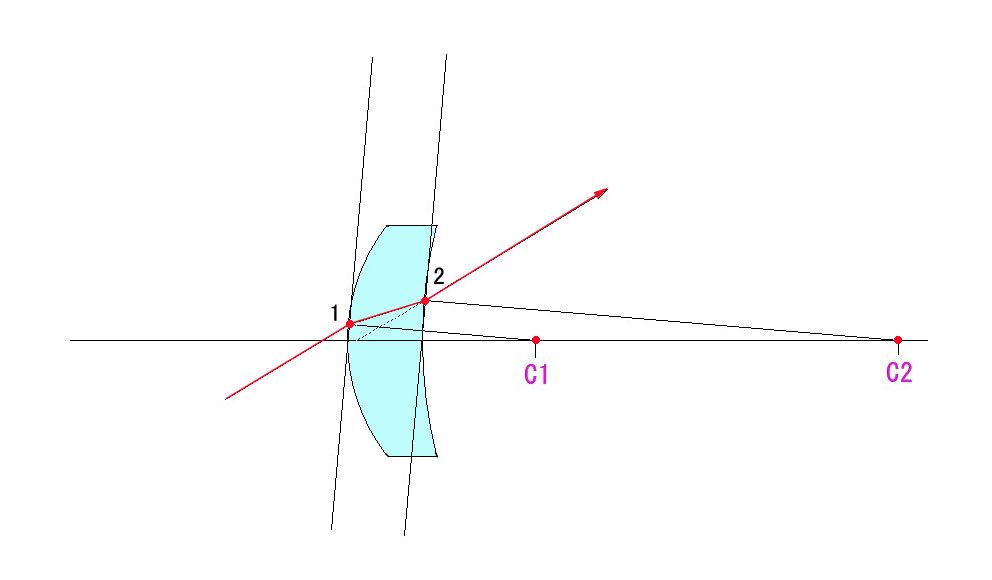
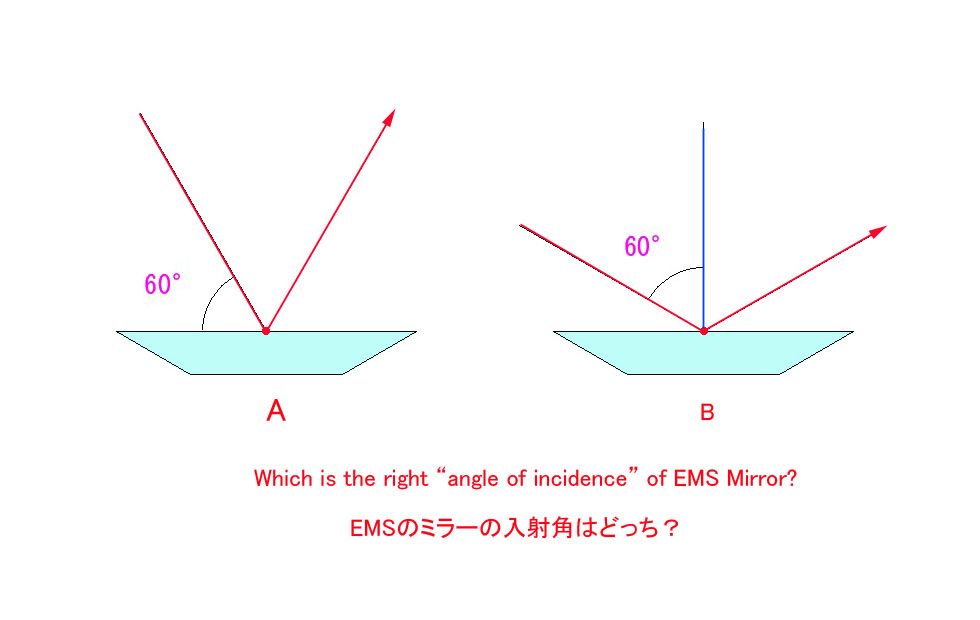
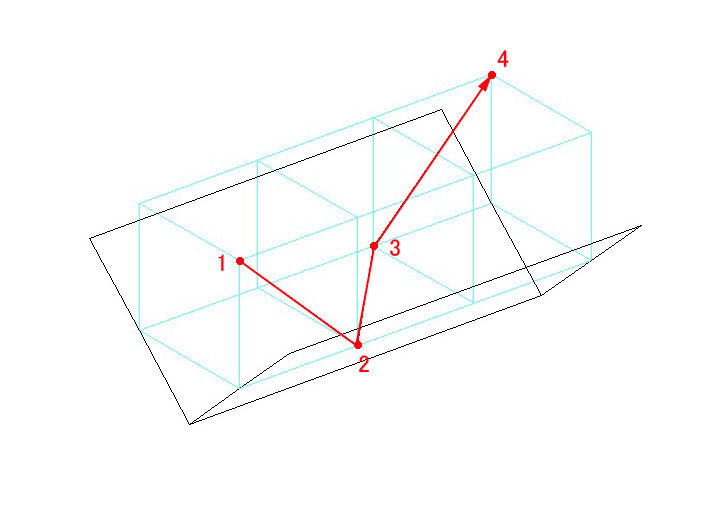
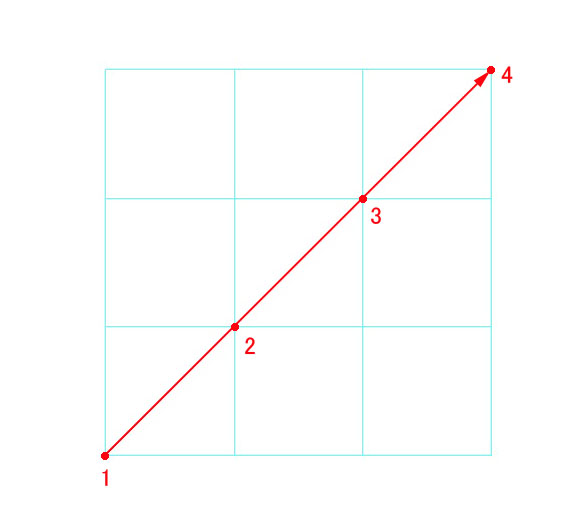
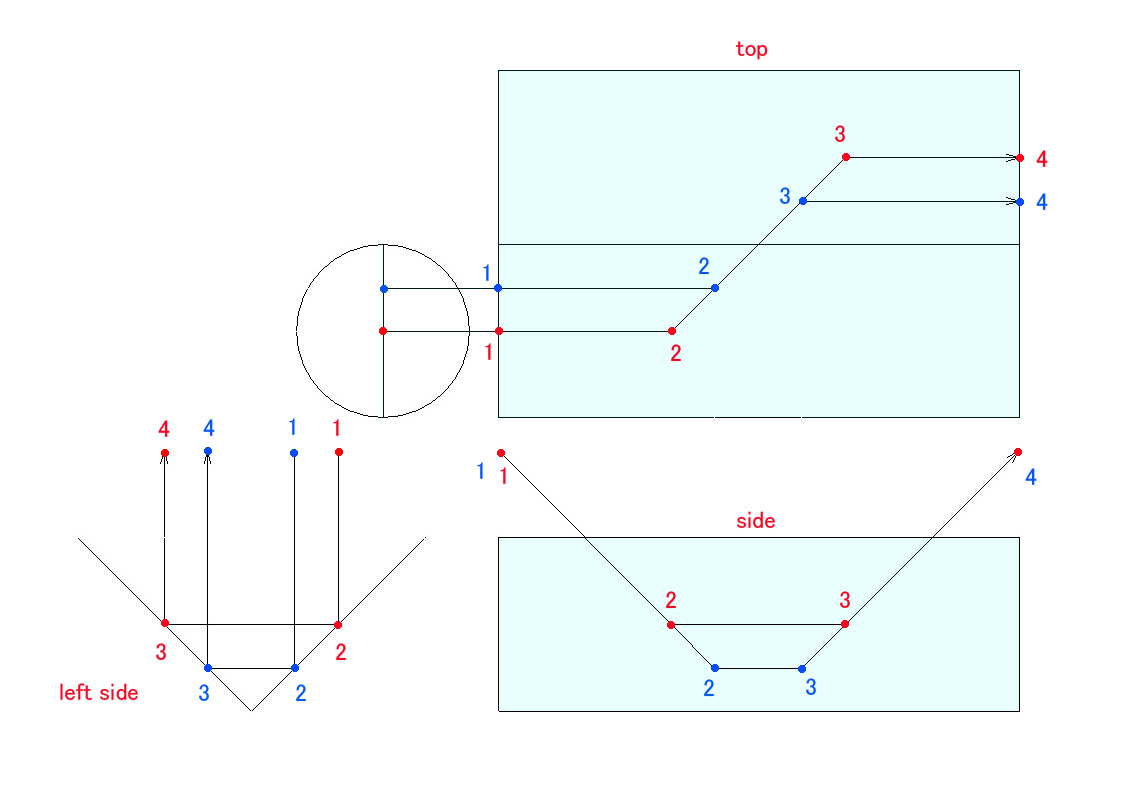
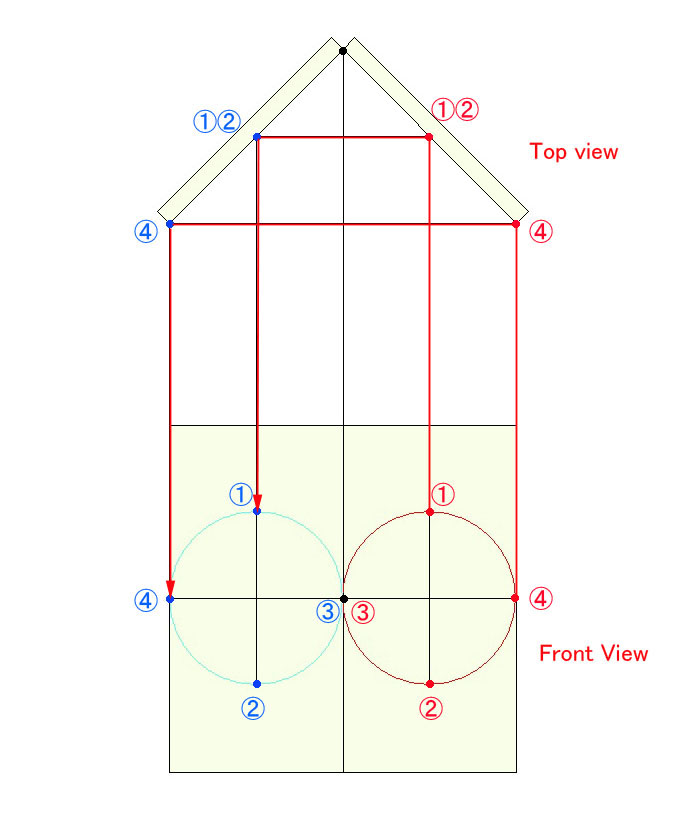
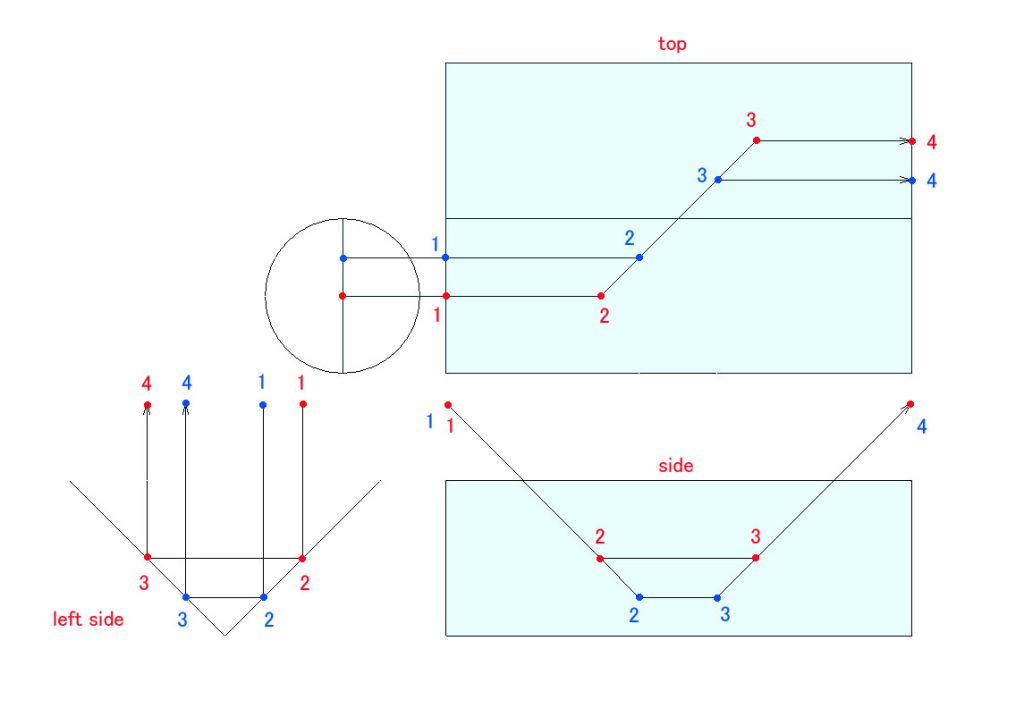
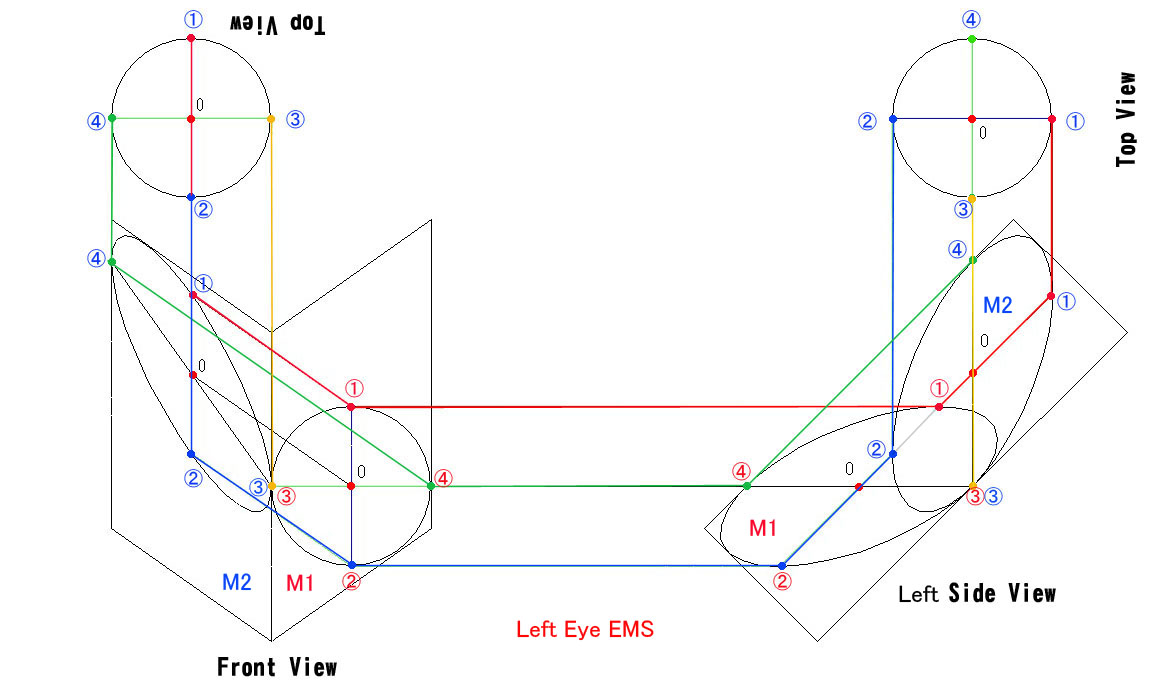
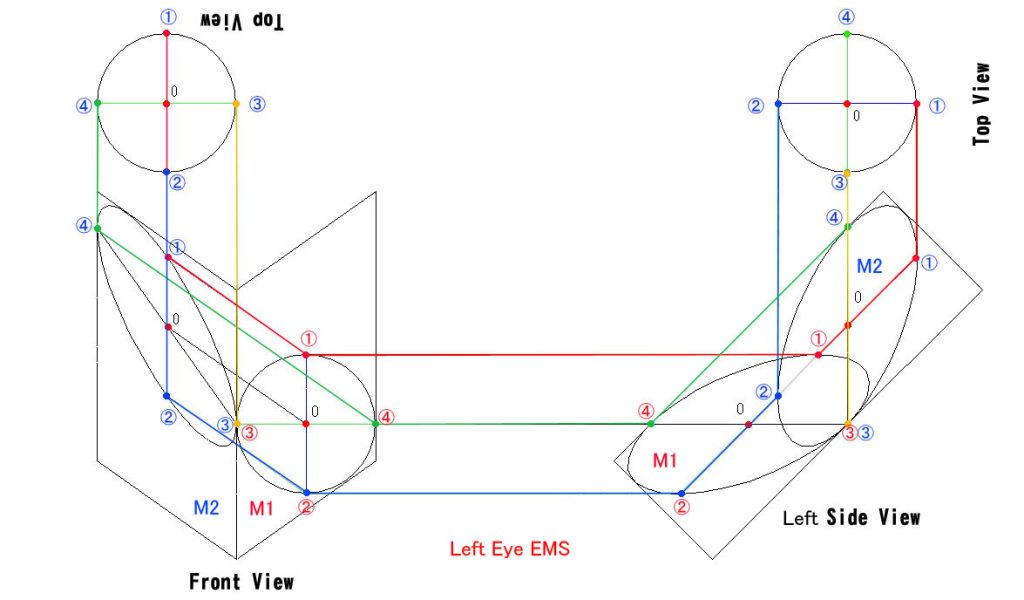
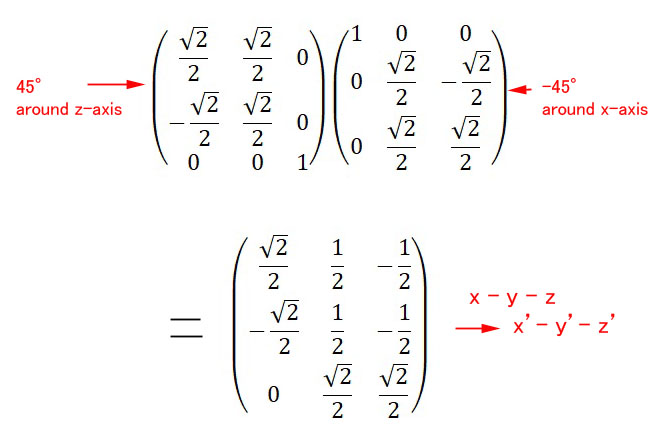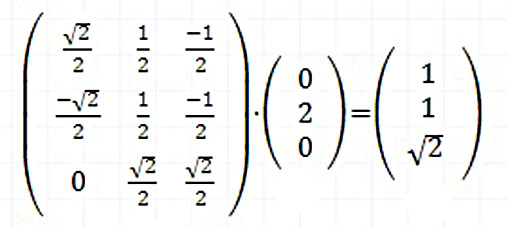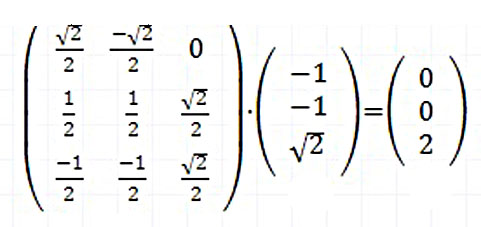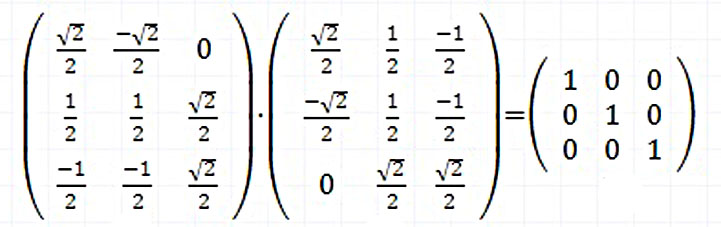　過去2回に渡って、像の向きの反転の様子を視覚的にご説明しましたが、今回は数学的に検証する方法をお示しします。
　まず、目標 AB と2枚鏡（説明略）を上の図のように配置します。座標軸 x-y-z をご確認ください。
AB→ の2枚鏡による像が下の図の A’B’→ のようになっていれば、物の向きが完全反転（上下左右反転）していることになります。90度対空なので、観察者はy軸の正の方向から負の方向を覗くことになります。偶数回反射なので、裏像にはならないため、天地方向の反転を示せば、上下左右の反転を証明したことになります。
　2回反射後の像が本当に A’B’→ のようになっているかどうかを、検証してみましょう。
上の図の座標軸のままですと、計算が複雑になるので、座標軸を都合の良い位置に回転させます。最終的に、下の図の x’-y’-z’ のように座標軸を回転させると、（新座標軸での）AB→ の成分 (a, b, c) が、2回反射後に (-a, -b, c) のように、ｘ座標とy座標だけが符合を反転するだけになります。
　具体的には、まず x 軸の回りに－45度（時計回り）座標軸（全体）を回転させ、次にz軸の回りに+45度（反時計回り）座標軸を回転させると、下の図の x’-y’-z’ となります。この作業は、x’z’平面が第1ミラー、y’z’平面が第2ミラーと一致するためのものです。
　反転作業が終わったら、座標軸を元にもどすと、元の座標系での A’B’→ が求まるわけです。
　座標軸は動かしても、物は元の位置のままであることをご認識ください。お宅の南向きの窓から見た鉄塔が左斜め45度にあったのが、西向きの窓から見たら右斜め45度に見えた、というのと同じことです。物差しの当て方を変えるだけで、測定が極めて楽になるという話です。

　次回以降に、実際の行列計算を辿ってみることにします。

　矢継ぎ早になりますが、実際に計算を辿ってみましょう。
まず、座標軸の回転について、高校時代にやられたのを復習しましょう。
x-y 座標で原点の回りに、x 軸を y 軸の方向にθ 回転させる変換行列は、

cos θ　　sin θ
-sinθ　　cos θ

ですが、x-y-z 座標で表しますと、z 座標は元のままなので、

cos θ　　sin θ　　0
-sinθ 　　cos θ　　0
0　　　　0　　　　1

となります。x 軸、y 軸の回りに回転させる時も、同様のやり方になります。

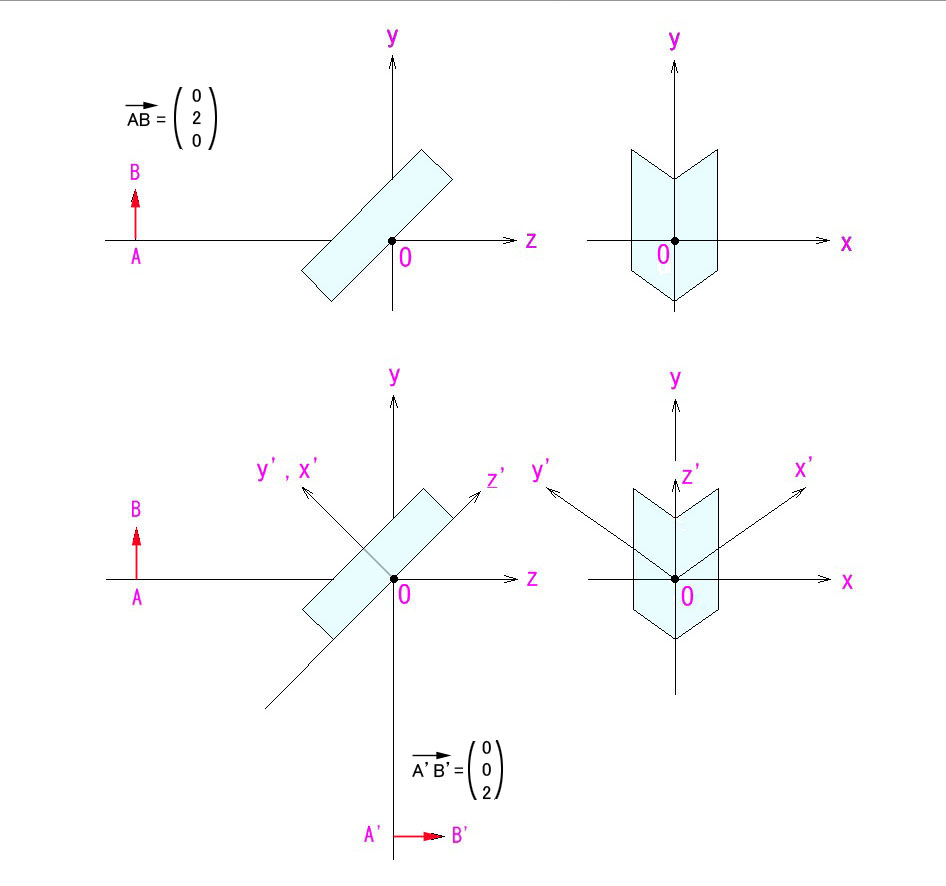
これが、上の図の座標軸 x-y-z を、x’- y’- z’ に変換する行列になります。
新しい座標軸 x’- y’- z’ では、AB→の元の方向ベクトル (0,2,0) が (1,1,√2) になります。

これが、図の2回反射後には、新しい座標軸で (-1,-1√2) になるわけです。

これが、x’-y’-z’ 座標での2回反射による変換行列です。

(-1,-1√2)が元の座標軸でどうなっているか、座標軸を元に戻して見ましょう。
座標軸を元に戻す行列は、前回の操作の逆をたどることになります。
回転の順序が極めて重要で、順番を間違うと全く違う結果になってしまいます。

この行列を使って、さきほど求めたAB→の2回反射後のA’B’→のx’- y’- z’ 座標での(-1,-1√2) が元の座標ではどうなるか、見てみましょう。

どうでしょう？　ちゃんと予想した通りになりましたね。
因みに、x-y-z を、x’- y’- z’ に変換した行列と、それを元に戻した行列は互いに逆行列になっています。
試しに、両者を掛けてみてください。単位行列になることが分かります。

　これならご理解いただけるでしょうか？
本を90度開いた形の2枚鏡です。昨日お見せした光路図、突き詰めると、これとほぼ同じなんです。
信じられますか？
　観察者の向きが180度変わったりしますが、観察者が２枚鏡の裏側に回り、上半身を前屈して股覗き風に見れば、正立像が見られます。180度対空型のEMSですね。
　注目いただきたいのは、①と②が、Open-Bookの谷の同じ深さで反射していること。そして、反対側のミラーでも、同じ深さで反射することです。この現象、昨日のモデルで全く同じなんです。
　それと、光路長が全て同じということ。Open-Bookの谷の奥深くでターンする光線は、代わりに横シフトが小さく、また、谷の浅い位置でターンする光線は横シフトが大きいため、それらが完璧に相殺されて、全て同じ光路長になるのです。

　Open-Book型2枚鏡、このように使っても、上記とほぼ同じ振る舞いをします。
折れ線の光線は、互いに平行のまま折れ曲がり、交差したり、もつれたりせず、実に無駄のない規則に従って最短路を進んでいます。溜息が漏れます。

　長い解説は読んでいただけないと思うので、簡単にご説明します。
左眼用のEMSの光路の解剖図です。
この図面だけを1年間くらいじっと見ていただくだけでも、いろんなことをご理解いただけるはずです。示唆する物があまりにも多いです。
　立体的に傾斜した光路の画面への投影なので、光線同士が交差しているように見ますが、実際はどれも交差していません。それぞれの光線が最短路を進んでいることが分かります。
　左の Front-View と、右の Left Side-View は完全に分けた方が良かったかも分かりませんが、Front View の開口円（真円）を Left Side-View とで共用させていただきました。
　開口円の ①→①→①→① と、同、②→②→②→② が光路長が等しいことが図面上からも明らかです。
（他の番号も同様（一部空間長を配慮する必要あり））
　また、EMSの光線の入射角（面法線と光線の角度）＝60度と、一般の天頂ミラー（入射角45度）よりもずっと反射面との角度が小さいため、開口径に対して非常に長いミラーを要求する点も、EMSの物作りとしてのハードルの高さを物語っています。ミラー同士の干渉を含めて、最大限のミラーを最小限のハウジングに収納するために如何に腐心を重ねた結果であるかをご理解いただけると幸いです。

　直感的に理解しにくい課題は、図を描いてみるのがまずお勧めです。また、図が描けるかどうかが、理解しているかどうかの試金石とも言えます。