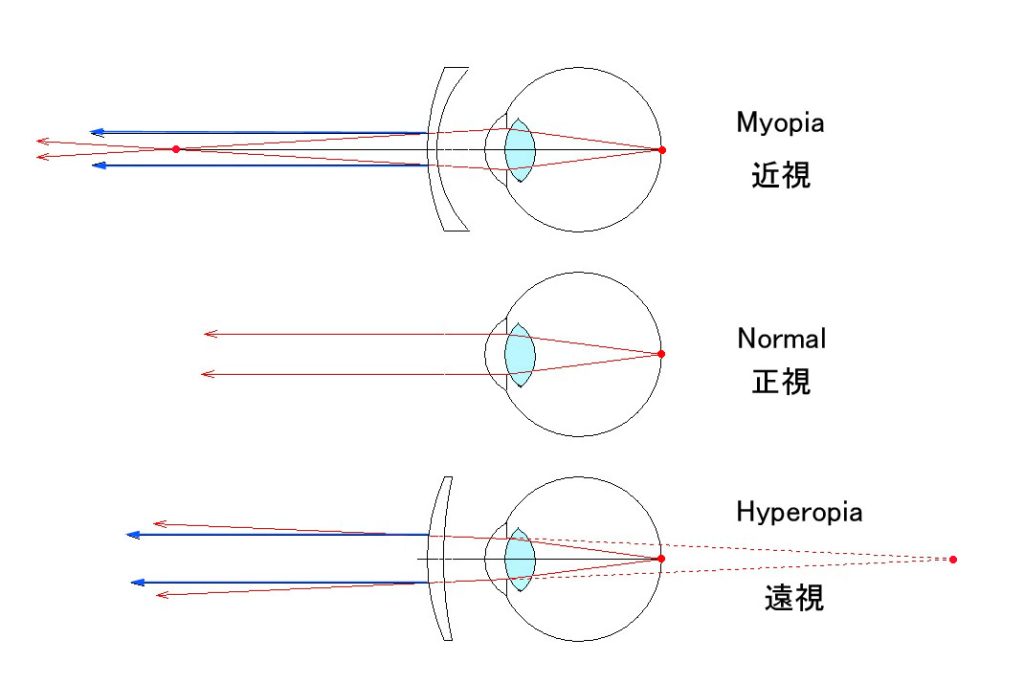
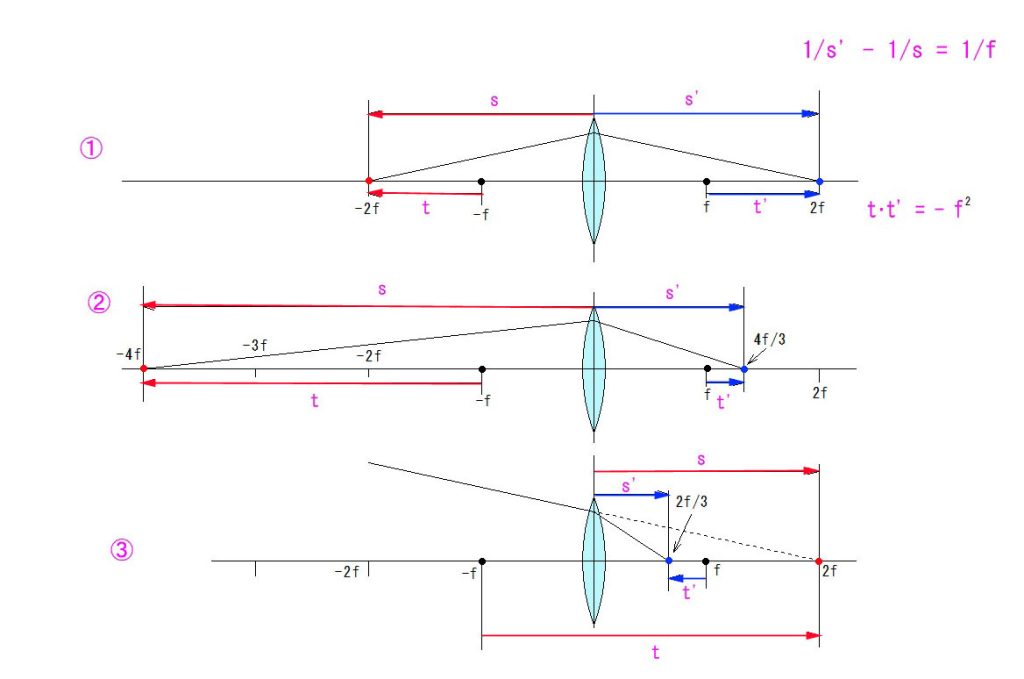
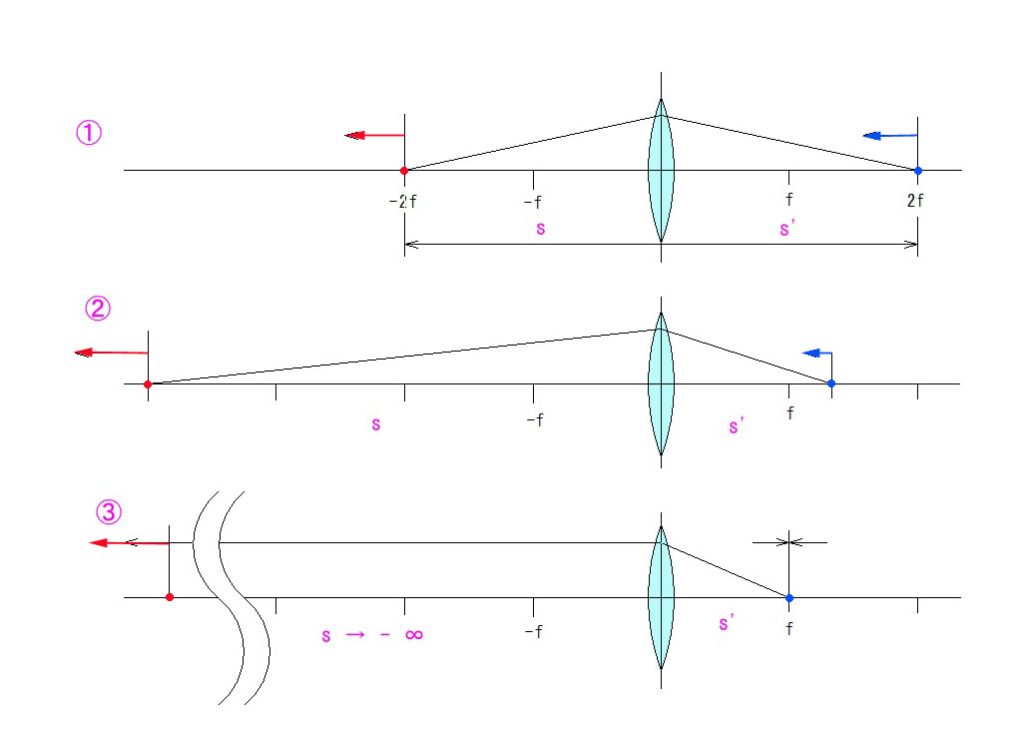
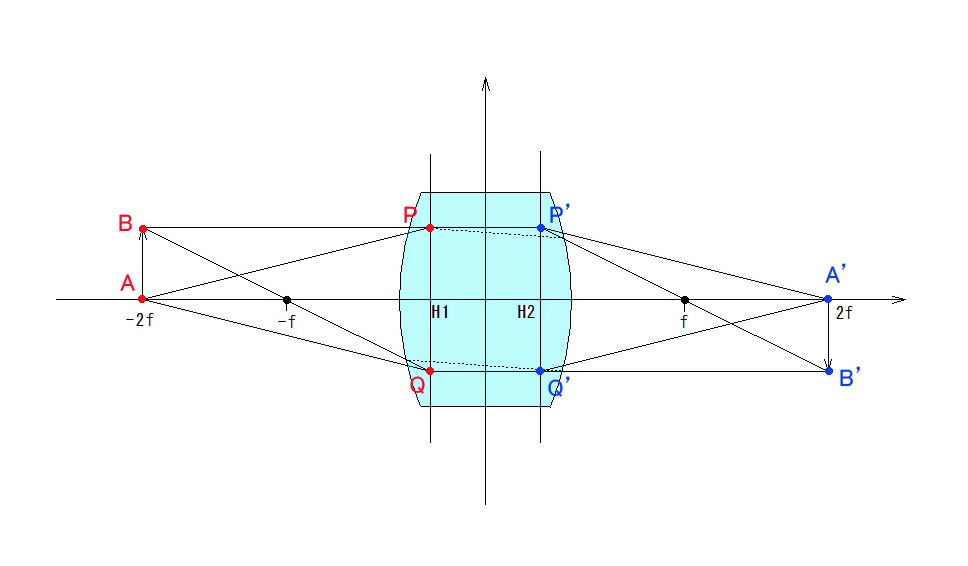
X-Y 調整ノブにリミット制限を掛けるのは、容易ではありませんでした。
ノブに原点復帰用の矢印シールを貼っていても、ユーザーさんが不用意に180°以上ノブを回転させたら、簡単に原点が迷宮入りになっていました。180°以上回すと、矢印の復帰の仕方で、ノブを1回転させてしまうからです。
ノブを回し過ぎないように、サイトで警告していましたが、違反者は無くならず^^;、リミッターをセットするに至った事情は、以前にもご説明した通りです。^^
以前に、テレビで、リサイクル事情のドキュメントをやっていて、ペットボトルのリサイクル工場が、キャップを除去する施設に**億円を投じたとが言っていましたが、それに似てるな!と思ったものです。 違反者がいなければ、不要な施設、装備なんですが、人間、仕方のないものですね。