寒冷の頃、皆さまにおかれましては皆様にはお健やかにお過ごしのことと存じます。
松本龍郎の双眼望遠鏡を応援くださっているユーザーの皆様、これまで有難うございました。お陰様で一月二十五日に無事四十九日の法要を終えました。
主人の双眼を愛し大切に使ってくださっているユーザー様のお声は私にも届いております。本当に嬉しく、心より感謝申し上げます。私も一段ギアを上げ、主人のいろいろを少しずつ供養しながら終わらせて行くつもりです。
店にある沢山の双眼の部品や材料などを手に取る度に工作機械の音が聞こえて来そうな錯覚を覚えます。
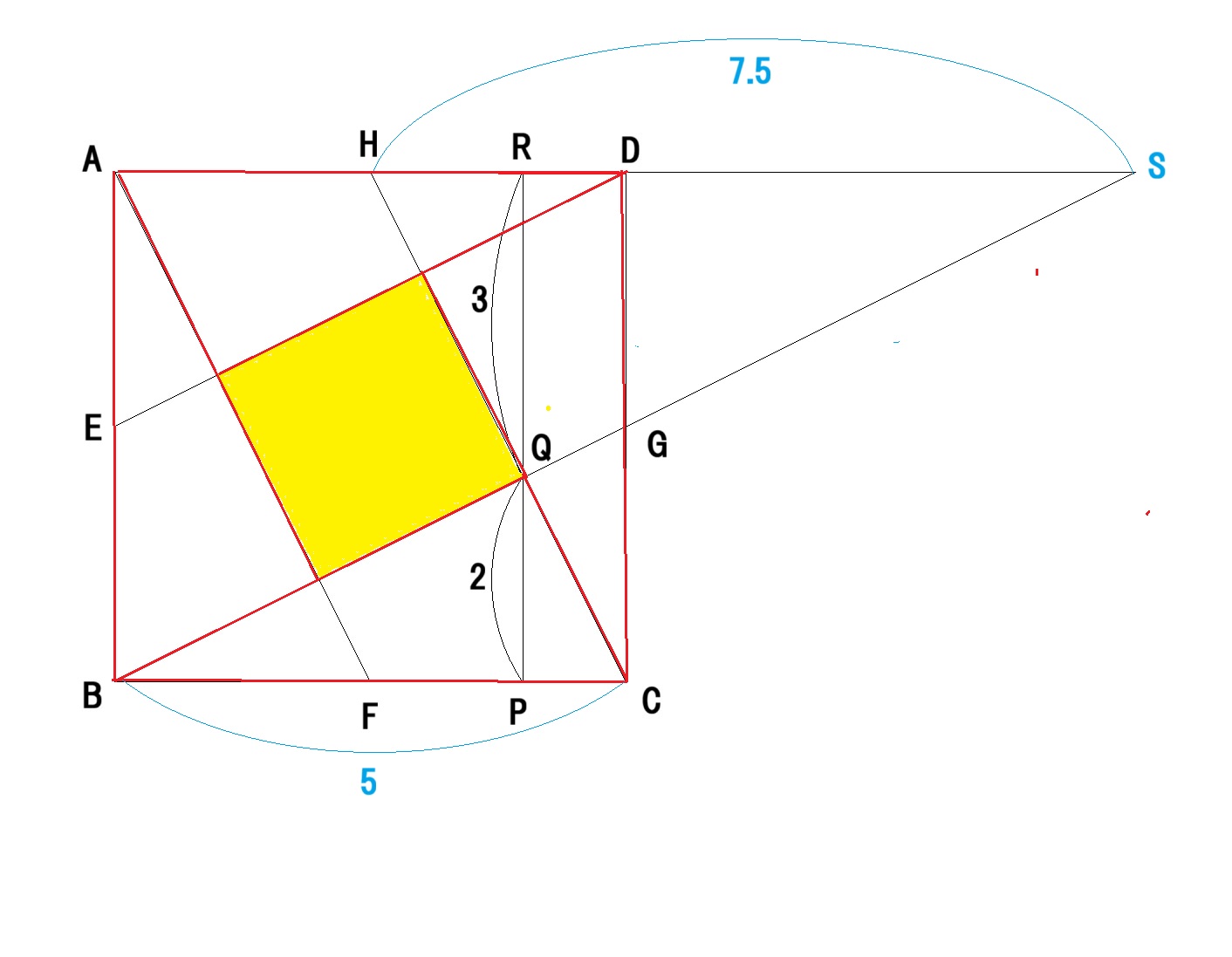
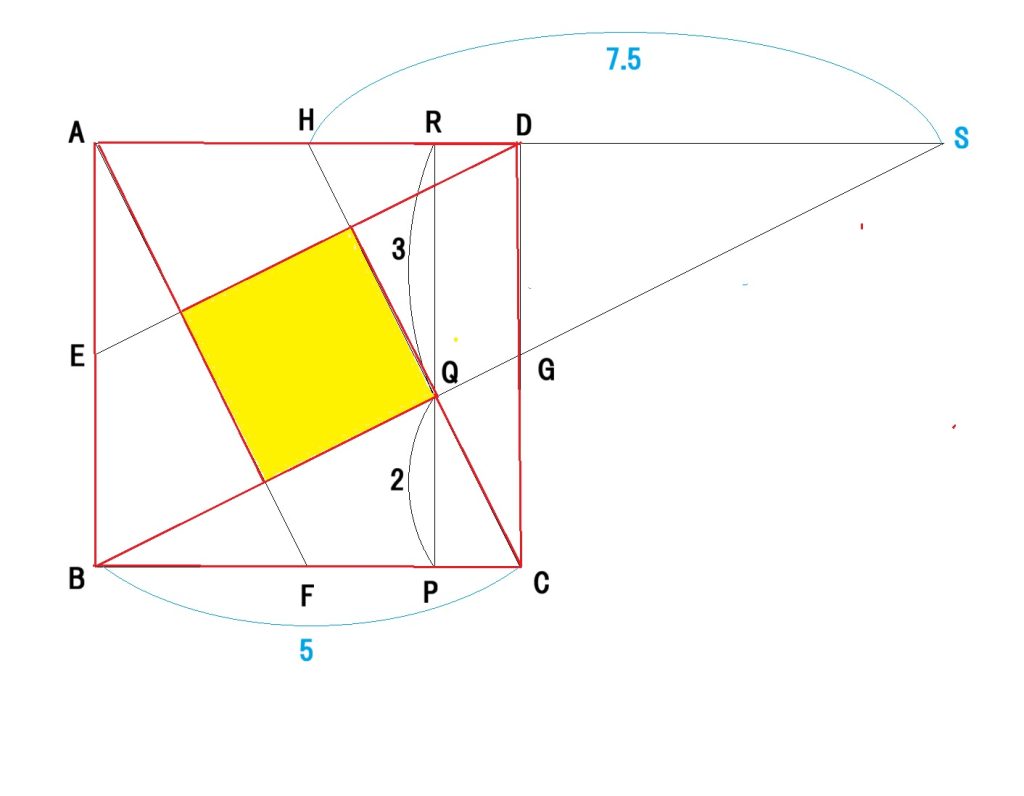
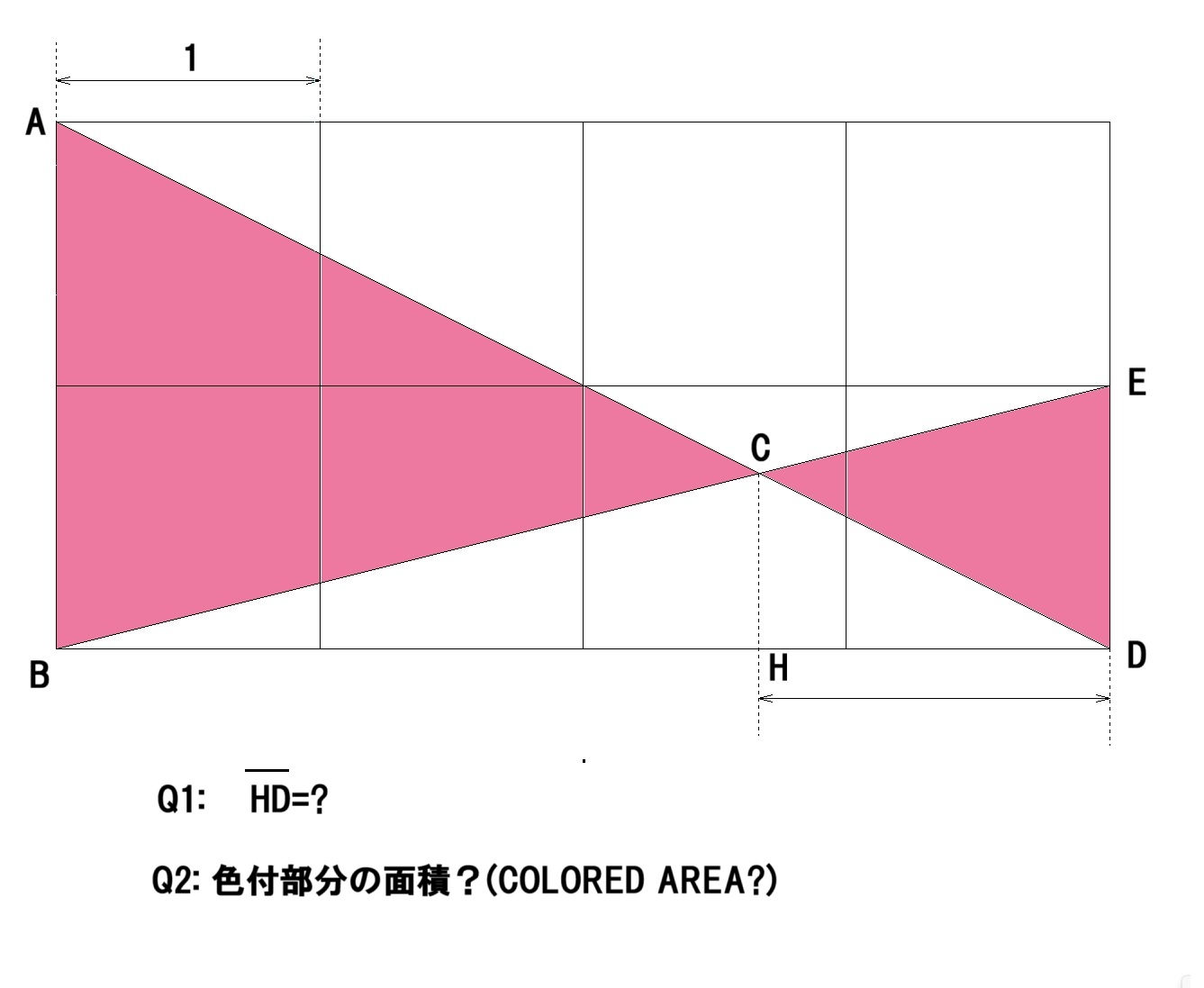
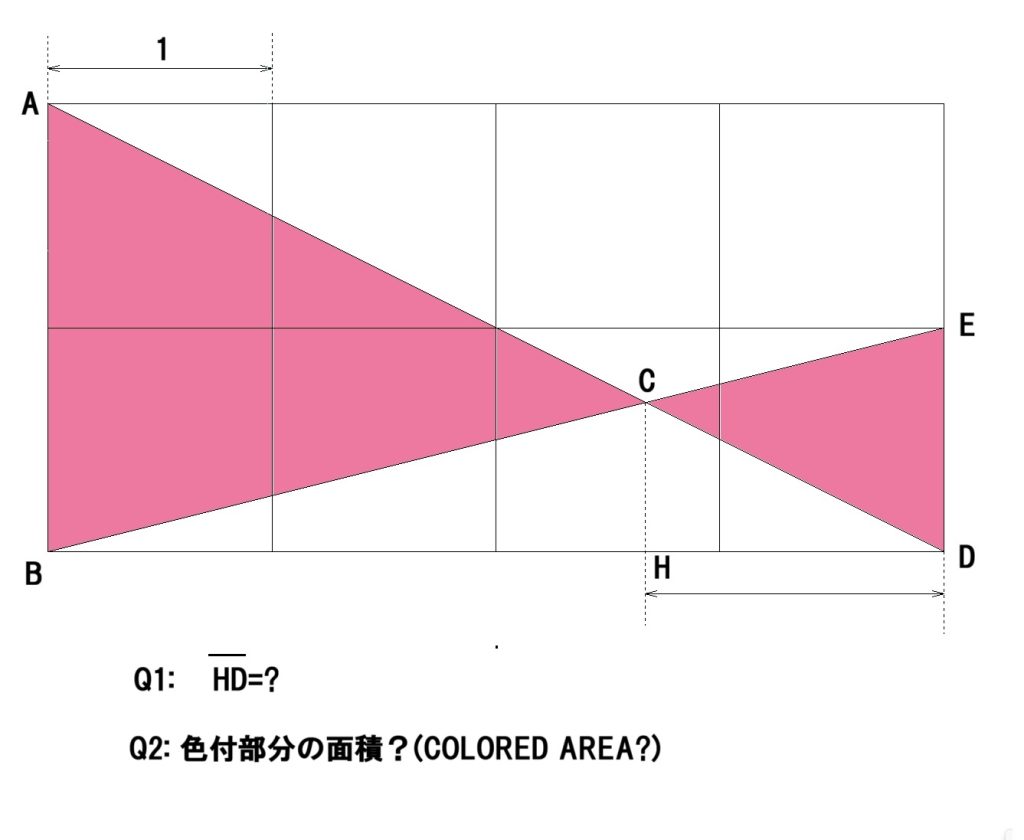
入院中「体は辛くても不思議と頭は冴えていて、次つぎにアイデアが浮かぶんだ」と言っていました。残されたノートに記された大量の計算式や図面がそれを物語っています。私が「究極の双眼が出来そう?」とたずねると「いんやー、まだまだだよー」と笑っていました。
これまで本当にありがとうございました。心から感謝申し上げます。皆様のご健康と幸せをお祈り申し上げます。そして皆さまのお手元にある双眼望遠鏡にエールを!
メガネのマツモト
松本尚子
I hope you are all staying healthy during this cold season.
Thank you to all the users who have supported Matsumoto Tatsuro’s binocular telescopes. Thanks to you, we were able to successfully hold the 49th day memorial service on January 25th.
I have also heard from users who loved and cherished my husband’s binoculars. I am truly happy and grateful from the bottom of my heart. I too intend to step up my game and gradually finish up my husband’s various tasks, while offering prayers for his memory.
Every time I pick up the many binocular parts and materials in the store, I have the illusion that I can almost hear the sound of machine tools.
While in hospital, he said, “Even though my body is in pain, strangely enough, my mind is clear and ideas come to me one after another.” The large number of formulas and blueprints written in the notebooks he left behind speaks volumes. When I asked him, “Do you think we can create the ultimate binoculars?” he laughed and said, “No, not yet.”
Thank you so much for everything. We sincerely thank you. We wish you all good health and happiness. And cheers to your binocular telescopes!
Matsumoto Glasses
Naoko Matsumoto