”内積”と聞いただけで逃げ出す日本人が多すぎる！
　その食わず嫌いで、多くの損失を被ることになりますよ、一生を通じて。
内積とは、ベクトルの対応成分を掛けて合計したものです。
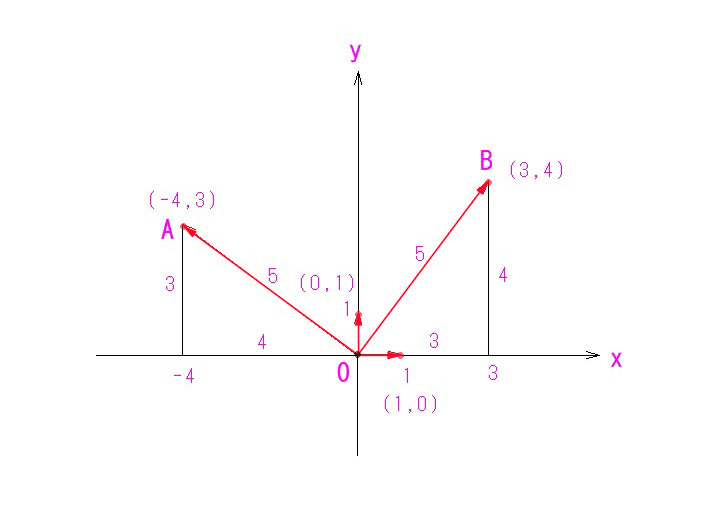
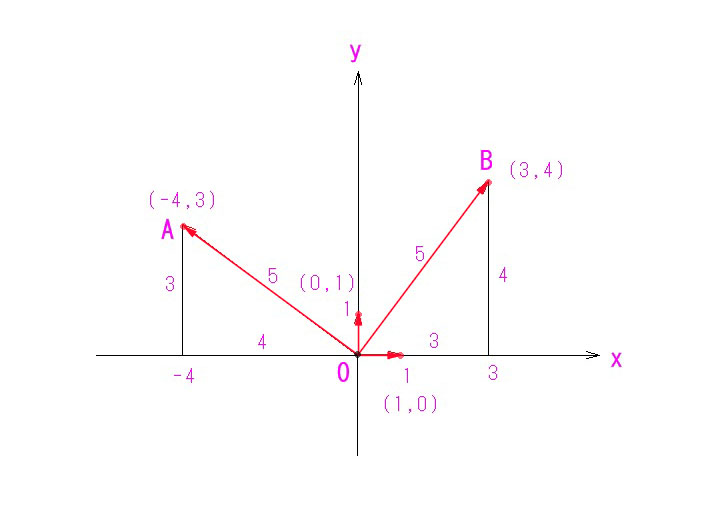
まず、x軸方向の単位ベクトル(1,0)と、y軸方向の単位ベクトル(0,1)の内積を求めてみましょう！
1×0 + 0×1= 0　で、内積＝0　です。
次に、ベクトルA(-4,3)とベクトルB(3,4)の内積を求めましょう。
-4×3 + 3×4 = 0　で、これも内積＝0 　です。
　そうです。直交する２つのベクトルの内積は、常に0になるのです。
3次元の任意の２つのベクトルA(a1,a2,a3), B(b1,b2,b2)も同じ計算方法で、
A･B（内積）＝a1×b1 + a2×b2 + a3×b3　で、直交していれば、値は常に0になります。
どうでしょう？　内積って簡単ですよね。　さあ、気を取り直して、昨日の講座をちゃんと読んてみてください！