この定理も、幾何光学ではよく利用するので、空気のように身に付いていないと、躓いてしまう。

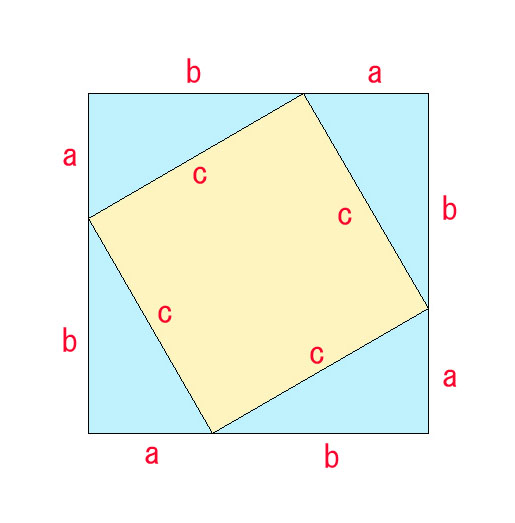
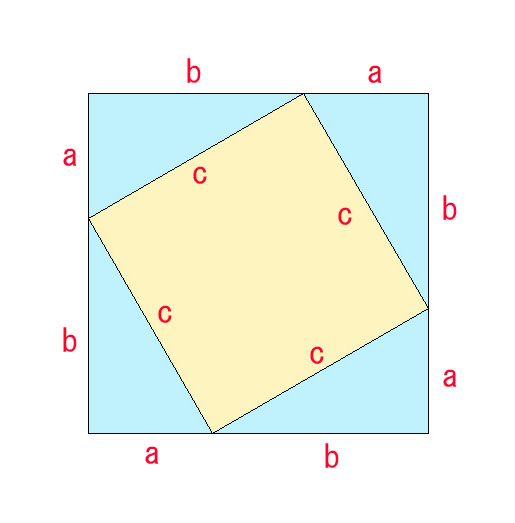
1.　大きい正方形の面積＝(a + b)^2 = a^2 + 2ab + b^2
2. 　小さい正方形（黄色）の面積＝　c^2
3. 水色の三角形×４の面積の総和　＝(ab/2 )×4 = 2ab

(1) の面積（大きい正方形）から (3) の面積（水色）を引いたのが、小さい正方形（黄色）の面積だから、
　　(1) – (3) = (2)
つまり、(a^2 + 2ab + b^2) – 2ab = a² + b² = c²

このことから、幾何光学で極めて重要な定理である、
　　　　　　　　　　　　　　　sin² θ + cos² θ = 1　も導かれる。

（ 蛇足ながら、c=1 のとき、a = sin θ , b = cos θ ）