意図的にスルーされている気もしますが、ここで終わるわけには行かないのです。
では、求めたシステムマトリックス（図中に記載 ↑）で何が分かるかについてご説明します。
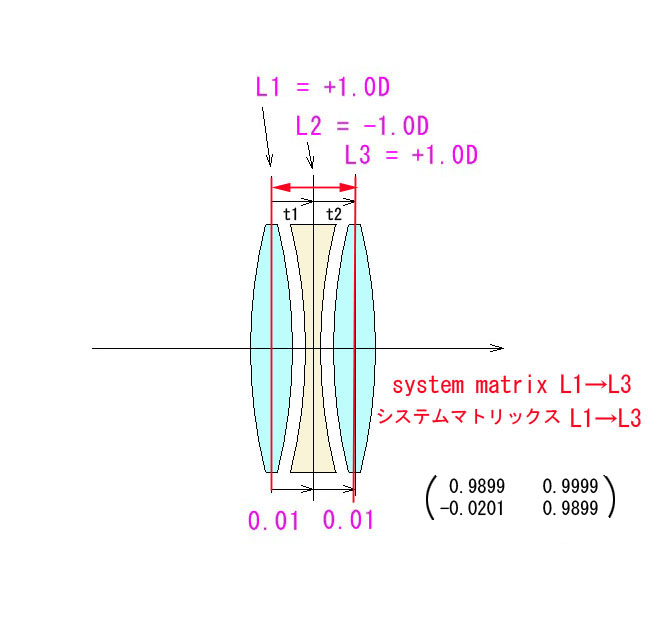
　まず、右上の成分 0.9999 から。合成パワー Φ（度数D)=0.9999D なので、
焦点距離＝1.0001m (1000.1mm)　( f = 1/Φ )
　エレメントの度数に対して、この程度のレンズ間隔だと、合成度数に関しては、ほぼ密着と考えて単純に3枚のレンズの度数を合計したのと、ほとんど変わらないことが分かりますね。
L1 から、+1-1+1=+1 。
　次に、主点位置を見てみましょう。
　以前にもご説明したように、システムマトリックス、
B A
C D　　の物側主点 E＝(B-1)/A 、像側主点 F＝(D-1)/A　により、

E = (0.9899 – 1)/0.9999 = – 0.01010101 = F　となります。
　( – ) が付いているのは、レンズ面よりも主点が中側にあることを意味します。
　ミリで言うと、約10mmレンズ系内に入った所なので、ほぼレンズ系の中央に、物側、像側の主点が位置していることになります。L2の凹レンズの中心ですね。

　では、次に、中央の凹レンズ L2 を除去したレンズ系のシステムマトリックス（図中 ↓ に示しました。）を見てみましょう。（各自で行列式を立てて計算してみてくださいね。）

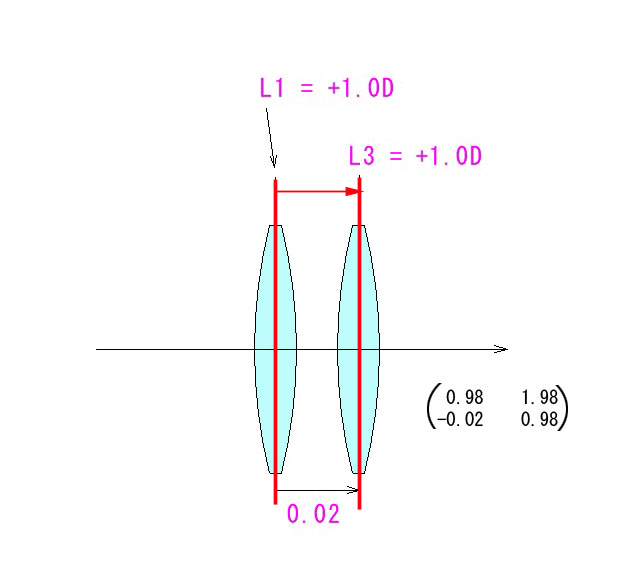
こちらの物側主点 E 、像側主点 F は、
E = (0.98 – 1)/1.98 = – 0.01010101 = F
　となり、何と、前問と全く同じ数値が出るではないですか！
　このように、完全シンメトリックな3枚玉の中央のレンズを除去しても、主点の位置は変わりません。
　合成度数＝1.98Dで、+1.0Dのレンズを2枚、20mm開けて配置したために、密着時の+2.0Dよりも度数がわずかに弱まりましたね。焦点距離では約 505mm。5mmほど長くなりました。
　このように、システムマトリックスを見ると、その光学系の顔が見えてくる。
　面白くないですか？？

次に、元の3枚玉のシステムに、左から光軸に平行で、高さ h=1 の光線を投入してみましょう。

計算の約束上、左から投入する光線の行列は、システムマトリックスの右側に配置することになります。
α=0　で、h=1　の入射光線です。
　それを計算すると、α’ = 0.9999 , h’ = 0.9899　となります。
　これが何を意味するかと言うと、
L1面に高さ h＝1 で投入された光線が、L3面上の高さh’ =0.9899の点から、傾斜角α’ = 0.9999の角度で射出するということです。
最終面L3とその結像点（焦点）までの距離 s’ =h’/α’ だから、
　　　　　s’ = 0.9899/0.9999 = 0.989999 (m) 　となるわけです。
　　さきほど求めた焦点距離より10mmほど短いですが、これは、焦点距離ではなく、像側の頂点距離で、焦点からL3面までの距離です。
これに、像側主点までの距離を加えたのが焦点距離ですから、今までの計算結果と合致しますね。

（＊投入する光線の h の初期値には制限はありません。途中で尺度を変えない限り、x 軸の尺度と統一する必要はありません。（理由は前の講座を辿っていただくと見つかります。））