準備運動ばかりやっている間に、桟敷席がほぼ空になってしまったことを実感しています。今回は、ご理解いただくというよりも、天文マニアが日々体験しておられて、感心があるはずの事象についてご説明します。意義が分かれば、基礎から理解しようとするモチベーションも高まるかと思うからです。
　望遠鏡を地上目標に向けた時、近い目標ほどピントが外（手前）に出て来る現象は、天文マニアなら、もはや空気を吸うように、日々実感しておられるはずです。
　「自室の窓からはせいぜい100ｍくらいまでの目標しか見られないが、無限遠の対象でのピント位置との差を把握したい。」
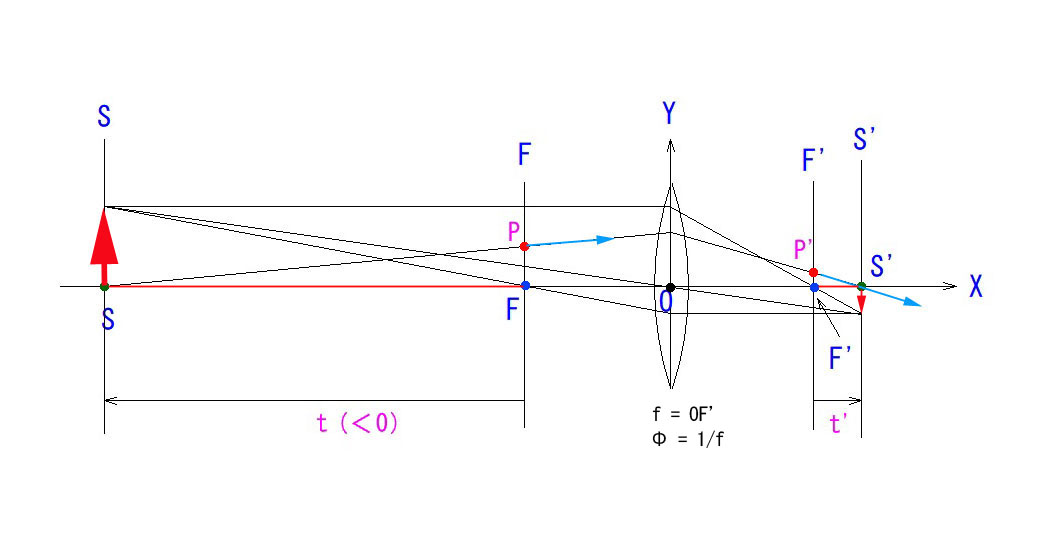
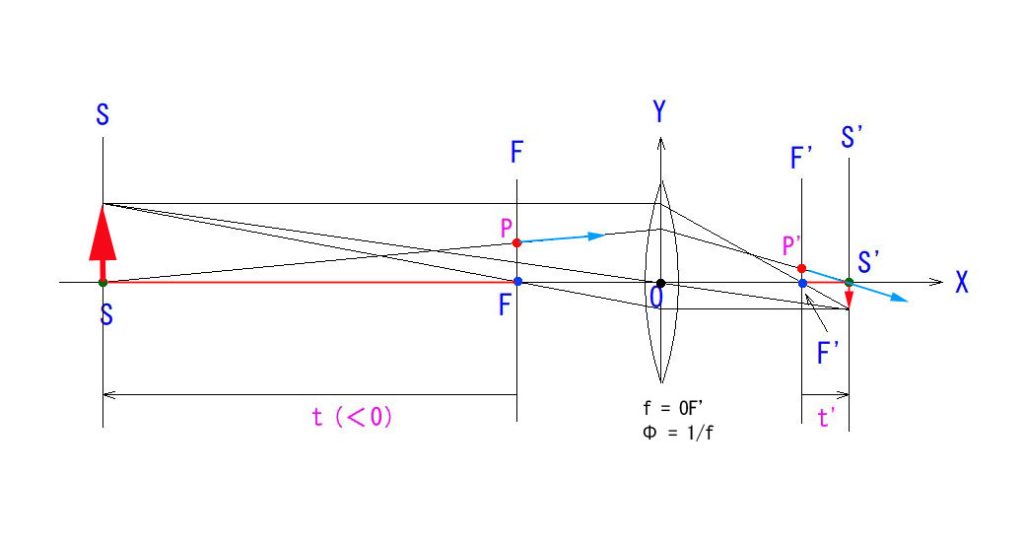
　↑こんなご経験が何度かあったはずです。バックフォーカスがシビアな場合には、これは深刻な問題となりますね。上図で言うと、t’ が知りたいわけです。　具体例として、焦点距離1ｍで、目標距離 (t+1)が101mのとき、t’ = 0.01m =1cmとなります。

　レンズを基点にした結像公式 　(1/s’ – 1/s = 1/f ) 　は皆さんよくご存じかと思いますが、２つの焦点（F,F’;物側、像側）を基点にした結像公式（ニュートンの公式）もあります。
上図によると、
( t･t’ = – f^2 )　というのが、ニュートンの結像公式です。右辺に( – )が付いているのは、t＜0とする約束のためです。（絶対値だけ問題にするのであれば、( – )は省いても良いでしょう。）
ニュートンの公式は、一般的な結像公式 (1/s’ – 1/s = 1/f ) に s’= f + t’； s= -f + t を代入して整理すれば得られますが、計算に慣れていない方は面倒かも分かりません。
　では、２つの焦点(F,F’)面を基点にした 焦点マトリックス と、物体面と像面 (S,S’) を基点にした 物像マトリックス を求めてみましょう。

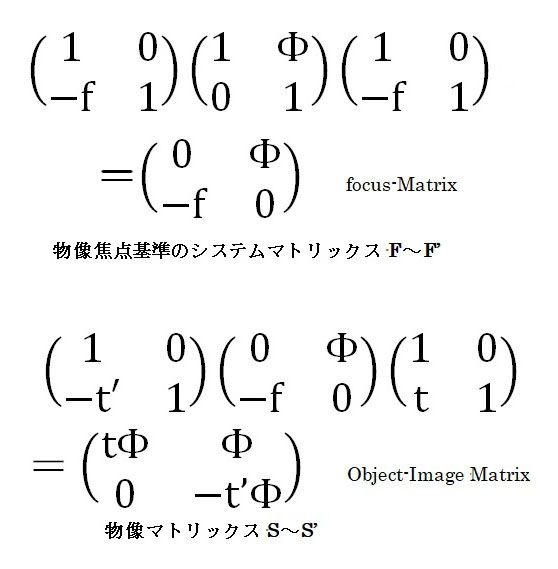
焦点基準(F-F’)のマトリックスからでもニュートンの公式は簡単に導出できますが、下の物像マトリックスではより簡単に導出できます。
以前にも、申しましたように、どんなシステムマトリックスも、行列式の値＝1 ですので、
t ･(-t’)･Φ^2 = 1　→　t ･t’ = -1/ Φ^2 = – f^2　　となります。
　また、物像マトリックスの右下の成分＝横倍率 M で、その対角成分＝1/M となることは以前にもご説明しましたが、これも注目すべき点です。左下の成分＝常に0です。

＊　行列の掛け算は、結合法則｛ A(BC)=(AB)C ｝は成り立ちますが、交換法則は成り立ちません ｛ ABC ≠ CAB ｝ので、ご注意ください。
　それから、左から右に掛けていくという行列の計算の事情から、各屈折や移行を代表する要素行列の並び順が実際の光線の進行方向とは逆になります。
　言い換えますと、光線は 左 → 右 ですが、、該当する要素行列は 右 → 左、と、全く逆の並びになりますので、混乱しないようにお願いします。

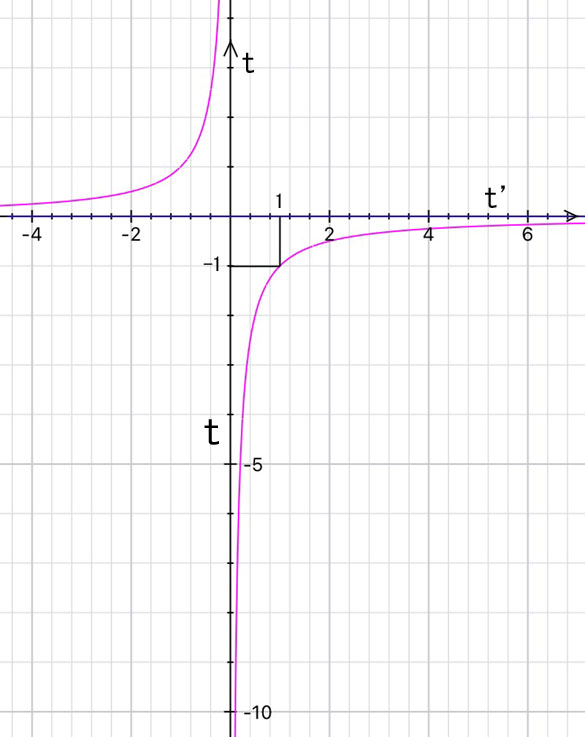
　最後に、t,t’ の関係を、焦点距離1ｍとして、グラフにしてみました。目盛りの単位＝1mです。
原点（座標軸交点）が焦点になります。ただし、t’ 軸については、一般的な焦点（像側）であり、t 軸については、物側焦点となるので、同じ原点であっても全く異なる点を基点としています。”ニュートンの公式”の最初の図を参照しながら見ていただくと、理解しやすいかと思います。

　左上（第2象限）のグラフは、望遠鏡対物ではほぼ使用しない領域です。t＞0ということは、物体が対物レンズの物側焦点より手前（焦点距離1mだと、対物レンズから1ｍ以内）なので、あり得ませんね。しかし、理論的にはあり得るわけで、その領域に入ると倒立実像ではなくて、遠い前方に正立虚像が出来ます。つまり、物体が１ｍ（焦点距離）以内に来ると、対物レンズはルーペになるわけです。

　ということで、天文マニアにとって、関係あるのは、右下（第4象限）のグラフで、しかも、天体望遠鏡で10ｍ以内の目標を見ることはまずないので、切り取ったグラフの枠外、ずっと下側で使うことになります。グラフはもはや曲線というよりも直線に近くなりますね。
　| t |=t’ （本例では1m）となる点がありますね。それぞれが、物側焦点、像側焦点から焦点距離分離れた点に位置するときです。
　ですから、レンズを基点にすると、それからの距離の絶対値が 2f となる点です。
　その時、物と像の大きさが全く同じになります。
　これを応用すれば、未知の光学系の焦点距離を非破壊（非分解）検査することが出来ます。