1. 後先になりましたが、準備運動からやりましょう。
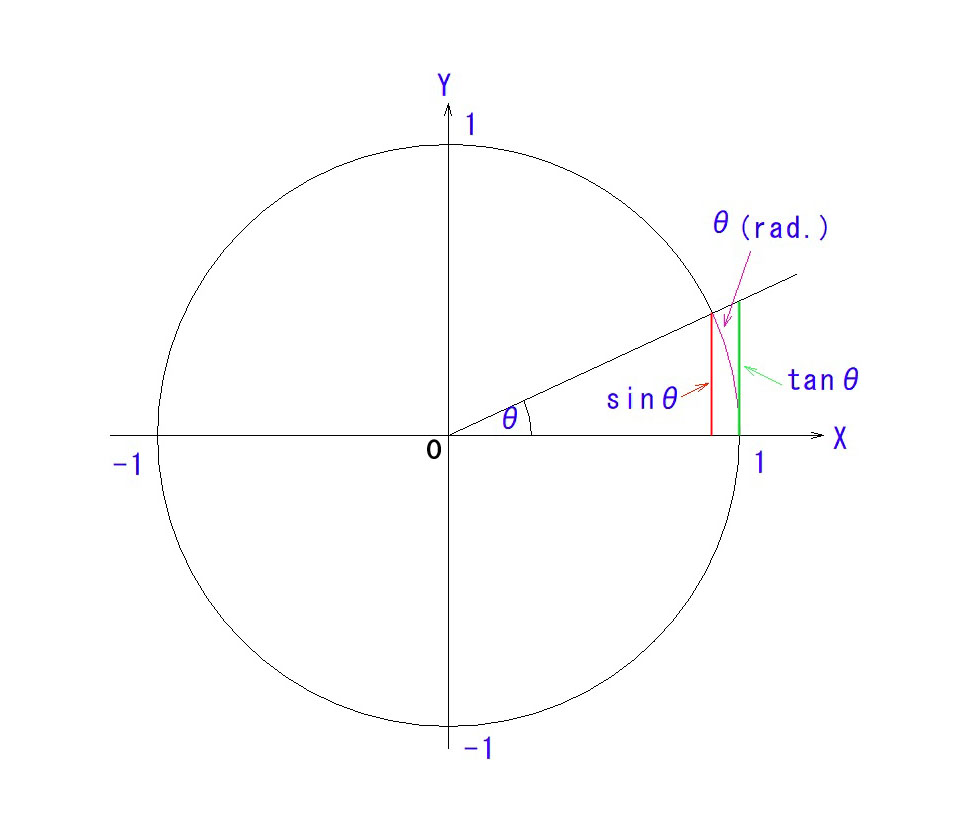
幾何光学で扱う角度は、断りが無い限り、一周360°の角度(度数法)でなく、ラジアンという単位(弧度法)の角度です。弧の長さが半径の何倍か?ということです。図の単位円(半径=1の円)の、θの弧の長さのことです。
2. そして、sinθは、図の赤い直線の長さ、tanθは緑の直線の長さです。
3. θ → 0 のとき、sinθ も tanθ も θ に収束するので、全てθとして扱っても差し支えないのです。
試しに、度数法の3°について、三者の数値がどうなるか、計算してみましょう。
sin3°=0.52335……..
3° =0.52359… rad.
tan3°=0.52407…..
3°付近でも、すでに3者の数値はかなり収束しています。角度がゼロに近付く(ほぼ光軸上)ほど、3者が収束することにご納得いただけたと思います。また、上図からも、グリーン、マゼンタ、レッドの3つの直線/弧 の長さが、θ→0のときに収束して行くことは、直感的にもご理解いただけるはずです。