今回は、理解できる、できない、の問題ではなく、すでに立証されている屈折の法則をご説明するものなので、素直に受け入れて、覚えていただく必要があります。

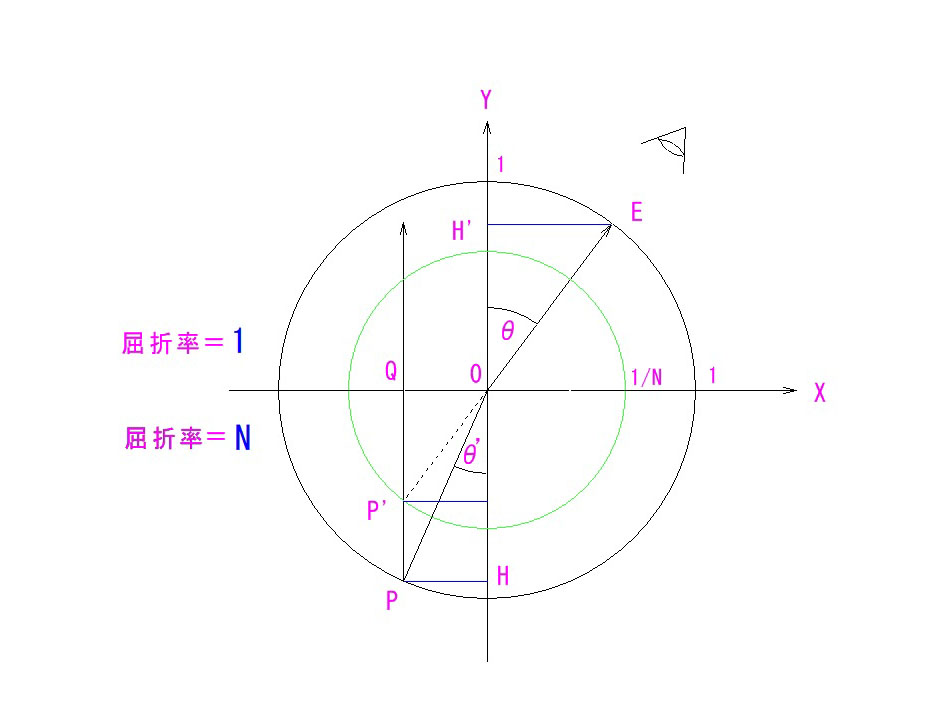
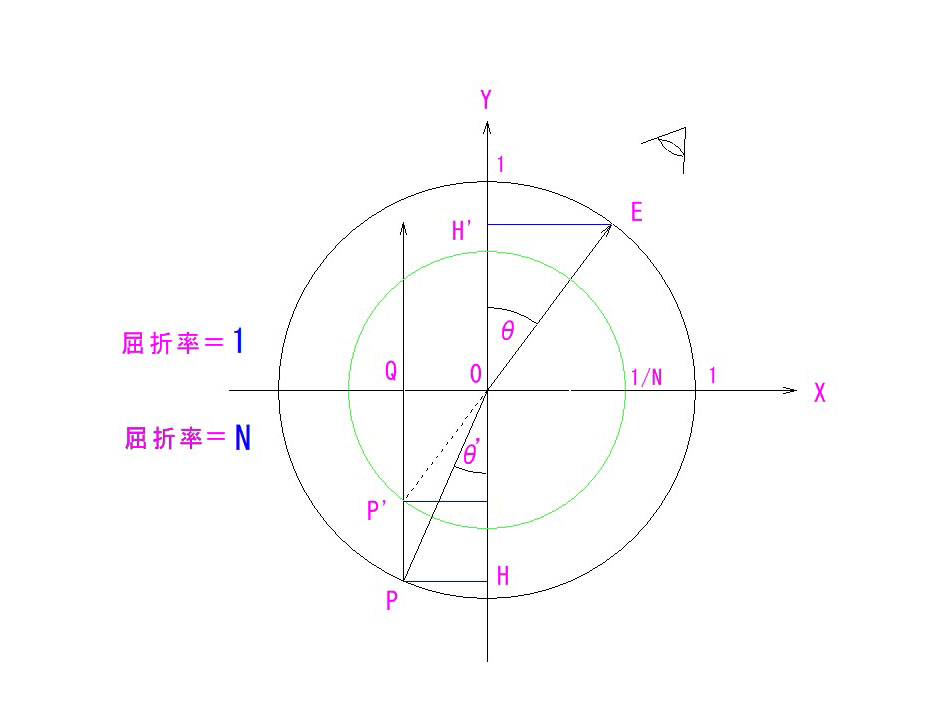
　屈折率がNとN’の界面に於いて、入射光線の入射角＝θ、屈折角＝θ’とすると、
Nsinθ＝N’sinθ’　となることはすでにご存じと思いますが、それを可視化すると、上図のようになります。よりシンプルにするために、N＝1（空気中）としています。
EH’/PH＝N　が屈折の法則、そのものになります。（OP/OP’=N と考えても同じ）

　Y座標の負領域が屈折率Nのガラスあるいは液体と考えてください。
Eから見ると、点ＰがＰ’に浮き上がって見えるわけです。
その浮き上がりは、OP/OP’=Nなので、厳密には QP/QP’ ≠ N なのですが、θ → 0 のときに、QP’ → OP’、QP → OP に収束するので、近軸領域では、QP/QP’ ＝ N　として差し支えないのです。

　ここでお分かりのように、反射の場合は、反射面が平面であれば常に完璧な結像を結ぶのに対し、屈折の場合は、たとえ界面が平面でパワーがゼロであっても、諸収差を免れないということです。
　従って、θ → 0 で、sinθ＝tanθ=θ (単位はrad.)の近似が成り立つ近軸領域に限定した、シンプルな公式 (Nθ＝N’θ’) を立てるわけです。この辺の近似の考え方が、多分、初学者を混乱、落胆させる要因だろうと思います。
　近軸公式だから、現実では役に立たないのではなく、無収差の理想光学系であれば、近軸の結像状態が全体を代表するし、そうでない場合は、光軸から離れた光線も同じ結像をするように設計努力するための目標、指針、骨格を提供するわけだから、近軸公式の存在意義は十分に大きいものがあるのです。