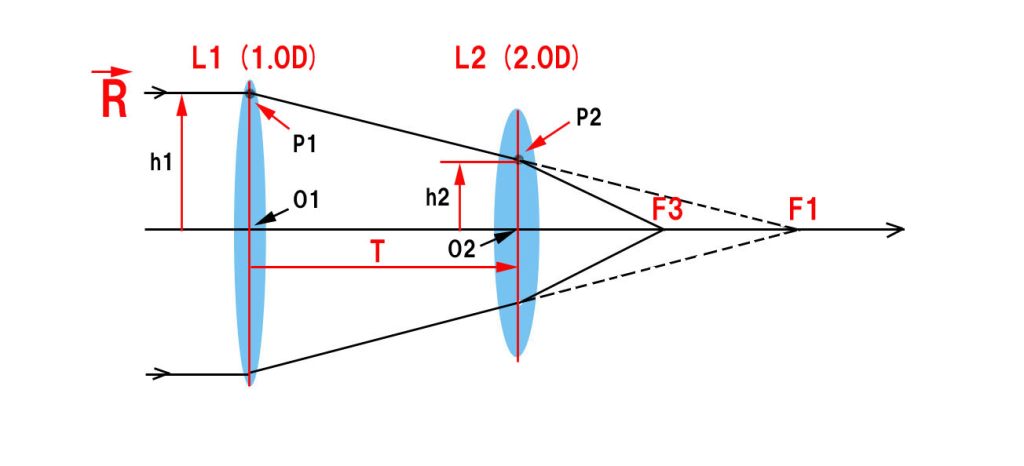
出来るだけハードルを低くするため、薄肉の2枚レンズ系（度数も配置も具体的に指定）でご説明します。入射光線から順に、レンズL1のパワー（度数；1/焦点距離m）＝1.0D、L2=2.0D,　レンズ間隔Ｔ＝0.5mとします。（f1=1000mm, f2=500mm）

　近軸結像の公式として 1/s’ – 1/s = 1/f —–式１ があり、それをレンズごとに駆使すれば、合成焦点の位置から、合成焦点距離、主点の位置等まで求められますが、レンズ枚数が増えるほど、計算が煩雑になって行きます。レンズを通過するごとに、レンズ間隔を調整したり、s’ の逆数を求めたりしないといけません。
　式1は、物点距離＝s　、像点距離＝s’、焦点距離＝f と置いていますが、ここで、1式の両辺に、”h”を掛けてみます。hは光線の指定位置に於ける光軸からの高さを表します。
すると、1式は、
h/s’ – h/s =h/f　　　となります。
　さらに、1/f =Φ（レンズのパワー）、また、h/s’ 、h/s　を、光線の傾き(tangent)として定義し、
h/s’＝α’、h/s＝α とすると、
α’＝α＋hΦ　と書けます。
（近軸式なのに、hを定義するのはおかしいのでは？と思うかも知れませんが、もともと、ｈは元の式の両辺に平等に掛けた数値であるため、単位はもとより、いくら大きな数値を設定してもかまわないのです。）

　αは、屈折する点に入射する直前の光線の傾き、α’は屈折後の光線の傾き、h は入射点の光軸からの高さを表します。傾斜角の正負は、光線同様に（レンズに対して）右側の結像点（物点）距離が＋になるように設定します。（右下がりの傾斜が＋）
　屈折直後の h’ は h と変わらないので、
h=h’　となります。
以上から、屈折マトリックス（行列）として、以下の行列が定義されます。（Φはレンズのパワー）

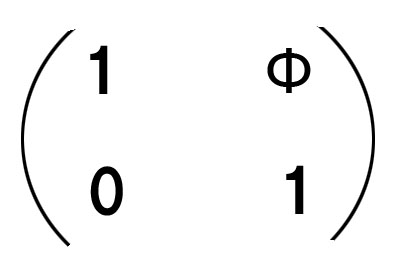
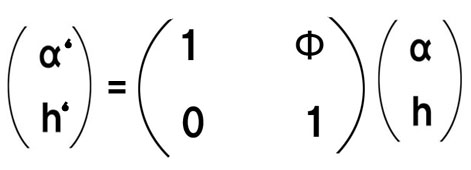
上記を行列表記でまとめると、こうなります。↑

レンズL1とＬ2の間は屈折が起こらず、hだけが変化するので、
α’＝α、h’=h-αt となります。
行列で表記すると、

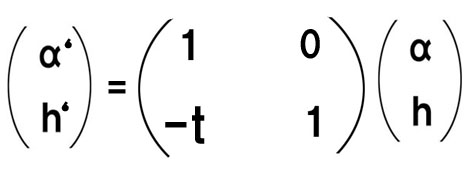
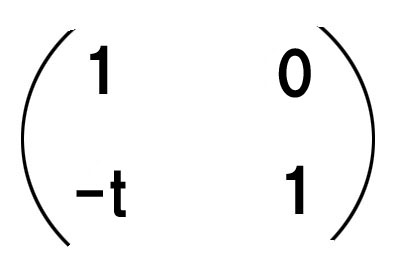
　　　　　　　　　　　　を、移行マトリックスと言います。
　両マトリックスとも、行列式の値は”1”であり、いくら掛け合わせても、結果の行列の行列式も常に1であることは、注目に値します。それを利用すると、一見絶望的に複雑な主点位置の計算も、いとも簡単に解けるわけです。

　お察しのように、レンズが何枚になろうと、屈折と移行のマトリックスを順に掛け合わして行けば、焦点位置、距離、途中の光束の太さから主点位置まで、簡単に求めることが出来るわけです。
　では、実例に則してやってみましょう。
2枚のレンズのパワー(1/f）は順に1.0Dと2.0D、間隔＝0.5mとします。
（Dはレンズの度数単位で、焦点距離（m)の逆数。）

　行列の計算順序の都合により、上の光路図のレンズの並びと該当行列の並びが逆になっていることにご注意ください。
（　　）は、右端から左向きに、L1の屈折マトリックス→Ｔの移行マトリックス→L2の屈折マトリックスとなります。この掛け算を行うと。

となり、これを、L1～L2までのシステムｰマトリックスと言います。
(行列の掛け算は、結合法則は成り立ちますが (AB)C=A(BC)、交換法則は成り立たない ABC ≠CAB のでご注意ください。）
　このシステムマトリックスに、左から、高さ(h)＝1で、傾角＝0（光軸に平行）の光線を投入してみましょう。行列式は、

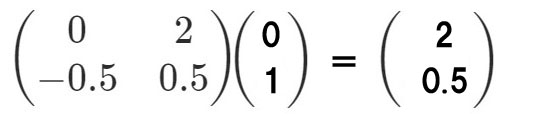
　これは、ｈ1＝1の高さでL1に入射した光線が、L2上の点P2で屈折した直後の光線の要素（傾角と高さ）を表しています。これから、この2枚レンズの合成パワー＝2.0Dであること、また、h2＝h1/2であることも分かります。
　また、この例に限らず、システムマトリックスの右上の成分が常にシステムのパワー（度数）になっていることにもご注目ください。

では、今度は、L1のパワーをA、L2のパワーをB、Ｔ＝レンズ間隔 として、L1～L2のシステムマトリックスの一般式を導いてみましょう。

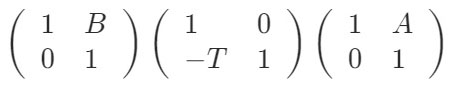
計算すると、

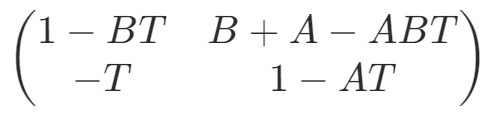
右上の成分がこの2枚レンズ系の合成パワーですが、何か、見覚えはありませんか？
（D=D1+D2 – D1XD2t　は2枚レンズの合成パワーの公式）

—-つづく