球面レンズに球面収差があることは、皆さんもよくご存じのはずで、3/11に、球面の球面収差を可視化した図をお示ししました。また、3/14にも、+10Dの平凸レンズの実際の球面収差も図示しました。
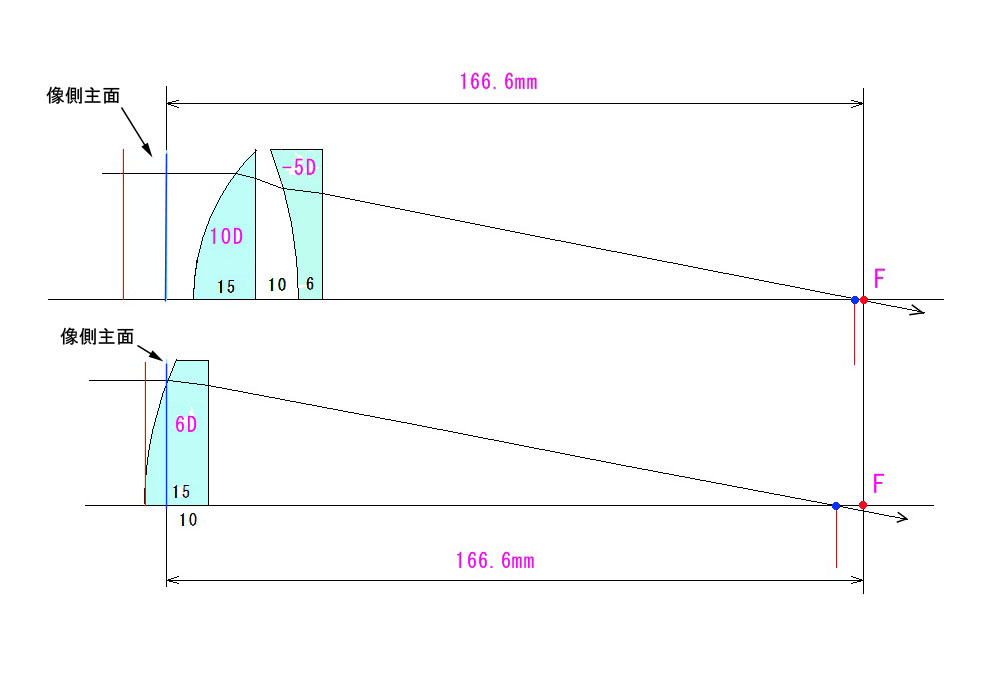
　今回は、3/14の+10Dの平凸レンズの後ろに、上図のように-5Dの凹平レンズを配置したらどうなるか？について検証してみました。
　F 点が近軸焦点（下の図も同じ）で、赤い点で示しました。下の、等価の平凸レンズに比べて、高さ30mmの平行光線の焦点位置がずっと近軸焦点に接近したことが分かります。

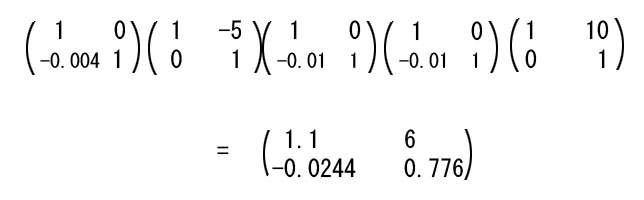
　システムマトリックスから、合成パワー＝6Dと出ましたので、比較をフェアにするため、元の10Dではなく、6Dの平凸レンズについて、下に近軸と高さ30mmのそれぞれの焦点を図示しました。

+10Dと-5Dのレンズを密着させると＋5Dのレンズになりますが、図の間隔に配置した結果、+6Dの合成パワーになりました。
　収差補正の考え方ですが、＋（凸）レンズの収差を、逆の収差を持つ ー（凹）レンズの収差でキャンセルしようというものです。一番分かりやすい例としては、
＋10のレンズにー10のレンズを重ねれば、球面収差を初めとするほとんどの収差がキャンセルされますね。同時にレンズとしてのパワーもゼロになりますがね。
　収差はキャンセルしながら、凸レンズのパワーを残す方法はないのか？という話です。
同じ凸レンズの度数でも、形状や配置で収差量が変化する実例を、昨日お見せしました。
球面収差が小さくなるように形状を配慮した凸レンズと、敢えて球面収差が大きくなる形状の凹レンズを組み合わせれば、凸レンズ成分を残しながら、球面収差を軽減、キャンセルできるのではないか？という話です。

　先日も申しましたが、今は優秀な無料の光線追跡ソフト（アプリ）が利用できる時代なので、こうした考察は無意味だとお考えでしょうか？　
　私はそうは思いません。そうした便利ツールを利用し始める前に、原理を体感しておくことは極めて重要なことだと思っています。

　蛇足になるかも知れませんが、上の要素行列についてご説明します。

　まず、光学面が4面で、間隔（厚みも含む）が3つで構成されたレンズ系になります。
　従って、厳密には、屈折マトリックスが4個と、移行マトリックスが3個の、合計7つの行列が連なるはずですが、上の要素は5つしか書いていません。

　凸平レンズの平面と、凹平レンズの平面です。それらの等価薄レンズとしての屈折マトリックス（両方が同じ）を書いてみると、
1　 0
0　 1　　となり、
　単位行列となることが分かります。（パワー＝0 だから）
　つまり、挿入しても何の変化も及ぼさないので、省略したわけです。