光が最小所要時間の経路を通ることから、所要時間の関数を立てて微分することで、純粋に代数的に屈折の法則を導入できますが、数式を敬遠される傾向が分かったので、今回は純粋に幾何学的、視覚的に納得いただけるモデルを作りました。
　光が光学的密度（屈折率）が異なる界面で屈折する事実—-①、また、平面波（無限遠からの平行光線）の波面（光線に垂直な面）は、屈折前後で崩れない—-② ことも前提として受け入れてください。
さらに、光の進行速度が屈折率に反比例する事実。—③ も認めてください。
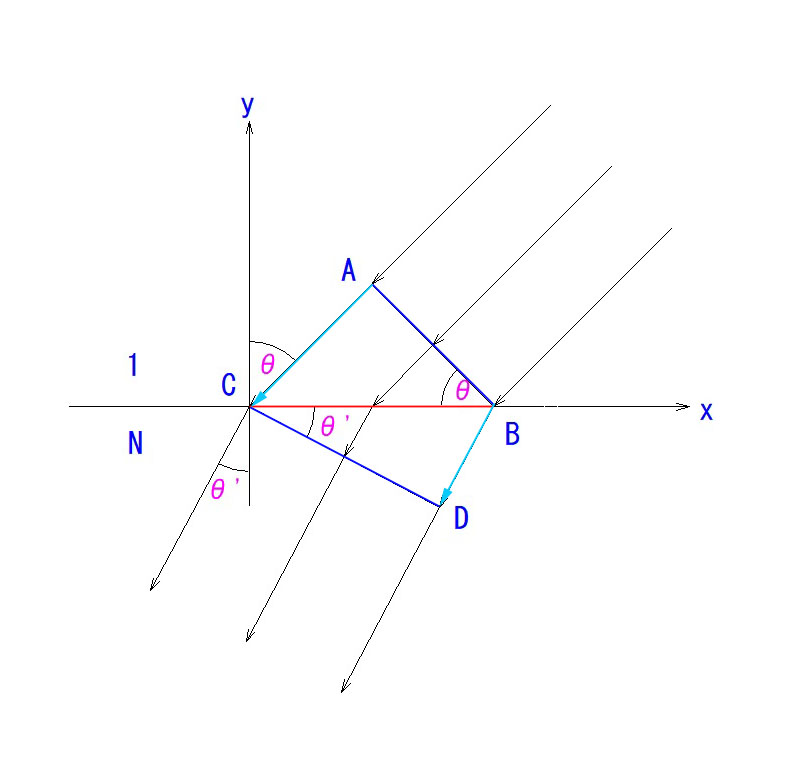
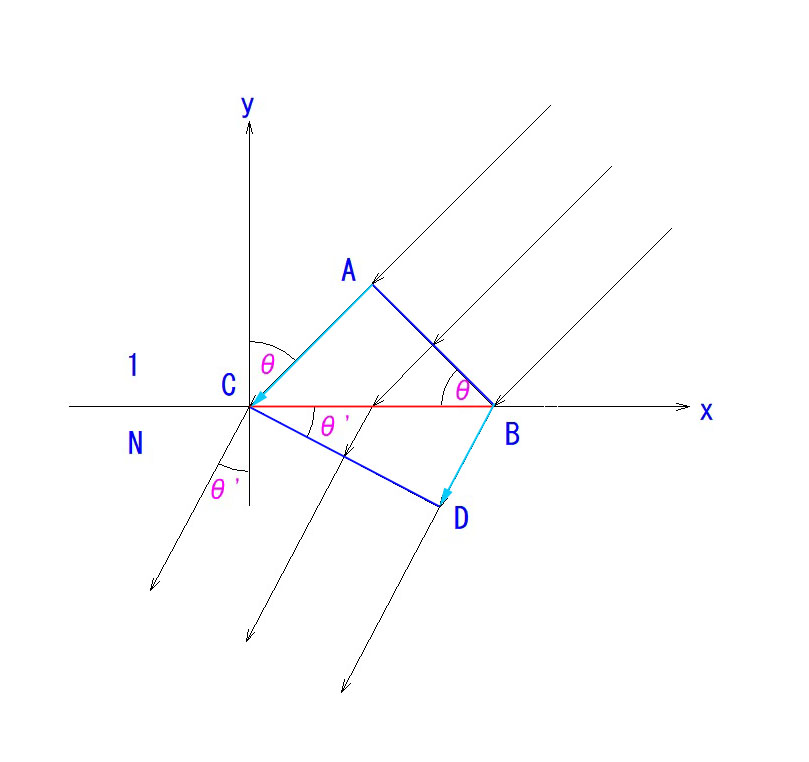
　つまり、AC間の光の進行速度は、BD間の N 倍になるということです。
　波面ABがCDに至る時、ACを移動する時間とBDを移動する時間が同じでないと、上の前提が崩れます。
　　これより、
　　sinθ = Nsinθ‘ が確定するわけです。(∵ AC = N･BD)
（ x軸より上が空気の例ですが、両サイドともガラス等（/ 液体）であれば、
　　Nsinθ = N’sinθ‘　）
＊BC=1 と置くと分かりやすいです。