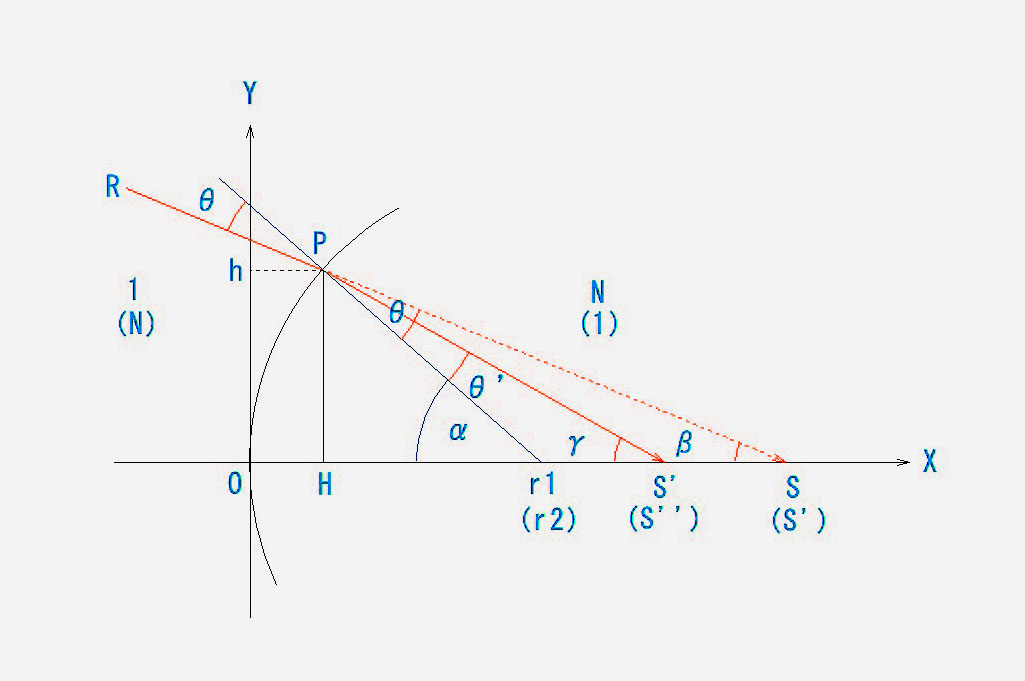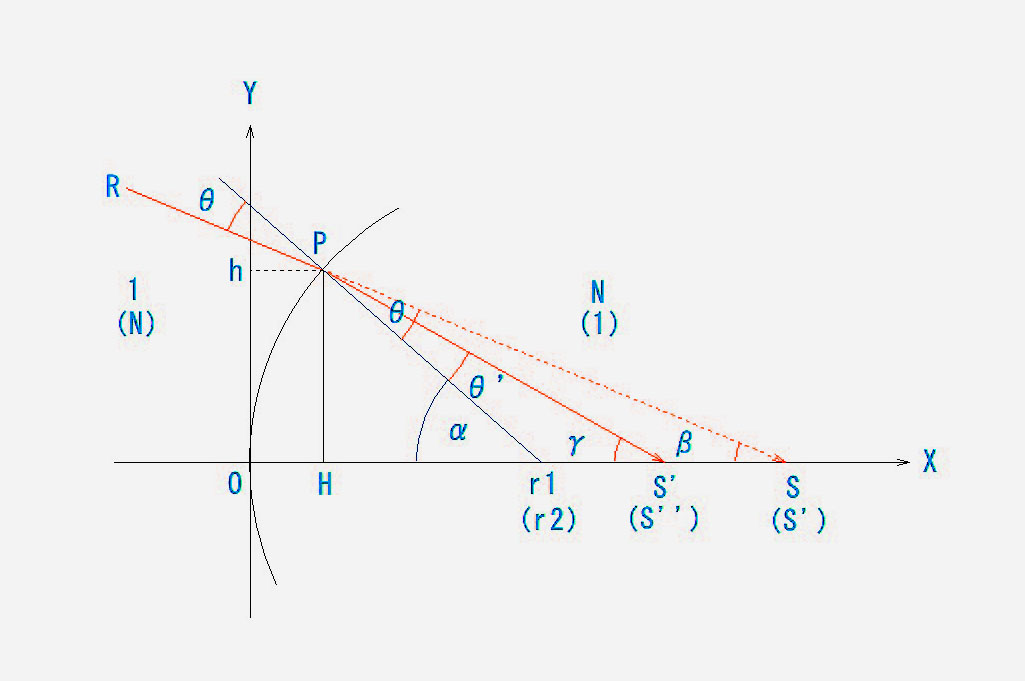
準備運動1,2が終わったところで、近軸結像公式を導いてみましょう。
まず、屈折の法則である、Nsinθ＝N’sinθ’が、近軸領域では、Nθ＝N’θ’となることを前回までにご説明しました。ここでは、よりシンプルにするために、N=1, N’ ＝N　とします。
Ｘ座標の負領域（屈折面まで）を空気中（屈折率＝1）とし、正領域の屈折率を1とします。
7．従って、θ＝Nθ’　となります。
近軸を前提としているので、屈折面（半径r）はY軸と密着しているはずですが、作図の都合上、見やすいように描いています。
8.　上図から、θ＝αーβ、θ’＝αーγ　となります。
9.　近軸前提なので、α＝h/r1、β＝h/S、γ＝h/S’　となります。
（Sが物点（虚物点）で、S’がその像点とします。）
10.　これらを(8)の式に代入すると、θ＝h(1/r1ー1/S)、θ’＝h(1/r1ー1/S’)　となります。
11. 　これらを(7)の式に代入すると、h(1/r1ー1/S)＝Nh(1/r1ー1/S’)　→　(1/r1ー1/S)＝N(1/r1ー1/S’)
　　　　となります。
12.　さらに整理して、N/S’＝1/S+(N-1)/r1　となります。
13.　次に、屈折率１とNの領域を反転させたモデルで計算してみます。
　　つまり、薄レンズの第2面による屈折の考察です。S’が第2面での屈折の新たな物点になり、その像点S”を求める式を立ててみます。
(12)の式のエレメントを入れ替えて、1/S”＝N/S’+(1-N)/r2　と表せます。
14.　これと(12)の式から S’ を消去すると、1/S”＝1/S + (N-1)(1/r1ー1/r2)、もしくは、
　　　　　　　　　　　　　1/S”ー1/S ＝(N-1)(1/r1ー1/r2)　と表せます。（近軸結像公式）
15. 　ここで、物点距離S→∞ とした時のS”が薄レンズの焦点距離 f なので、
　　　　　　　　1/f ＝(N-1)(1/r1ー1/r2)　となり、これが薄レンズのパワー（度数）になります。

●　r が入射光線に対して凹面の場合は、r ＜ 0 となります。X－Y 座標に忠実に正負を設定する限り、どんなケースでも式は破綻しません。

　ここまでご理解いただいてから、講座１に戻っていただきますと、より理解が深まるかと思います。
理解できないところがありましたら、その番号をお知らせいただけば、さらにご説明します。