前回の屈折の法則、分かりやすく工夫したつもりでしたが、分かりにくかったでしょうか?
反射の法則の方がずっと明快なので、先にこちらをUPすべきだったかも分かりません。
今度こそ、すぐに逃げないで最後までお付き合いください。
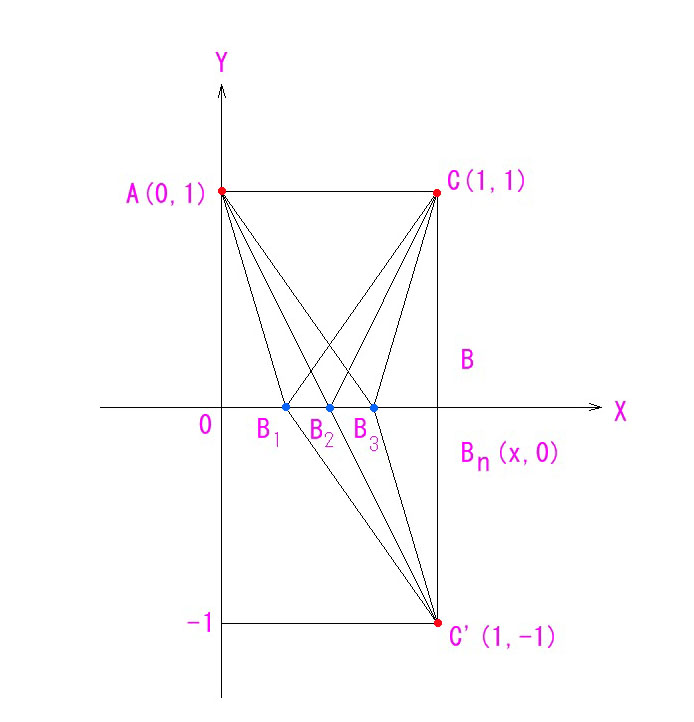
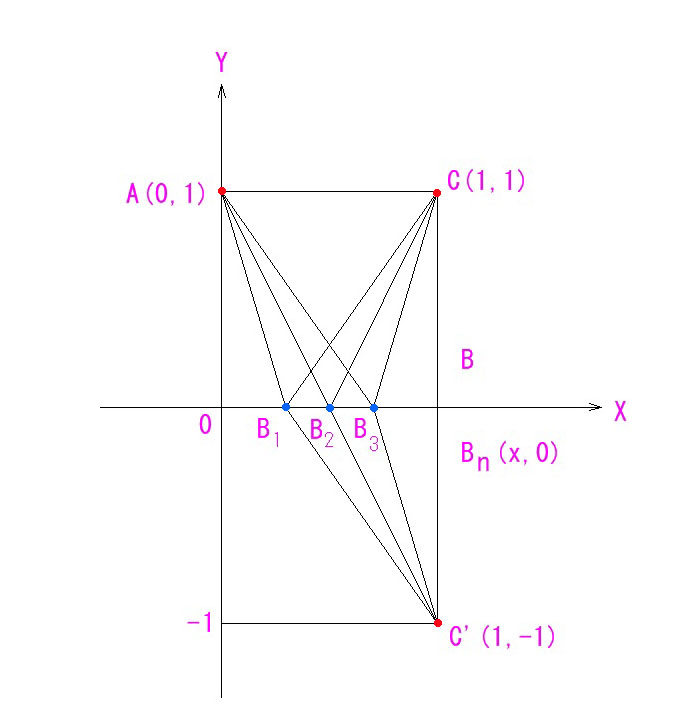
あなたの居る位置を A(0,1) とし、C に最短路で移動したいとします。
それは簡単で、直線 AC に添って進めば良いですね。
ここで、条件を付けます。Cに行く前に、X軸で代表される壁を一度タッチしてからCに行かないといけないとします。その最短路を考えてみましょう。
X軸の壁にタッチする位置 Bn (x, 0) は、0<x<1 の範囲で候補は無数にあるわけですが、その距離を考える前に、C の、X軸に対して対称な点 C’を作図しておきます。
すると、Bn C = Bn C’ となることが図から明らかです。
ということは、総経路長=ABn + Bn C = ABn + Bn C’ より、
ABn + Bn C’の最短路が 総経路 A-Bn-C の最短路となり、
直線AC’がX軸と交わる点B2 が最短路となるタッチポイントと言えるわけです。
このように、光線は常に最小所要時間の経路を進むことが分かっています。
作図に当たって、A,Cに具体的な座標を与える必要はなかったのですが、代数的に検証してみたい方のために、敢えて数値を与えました。