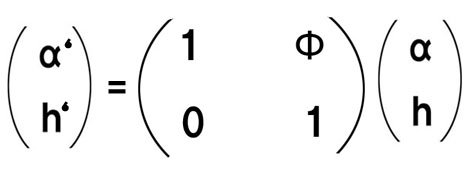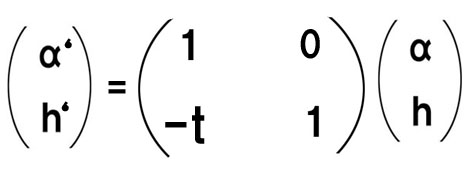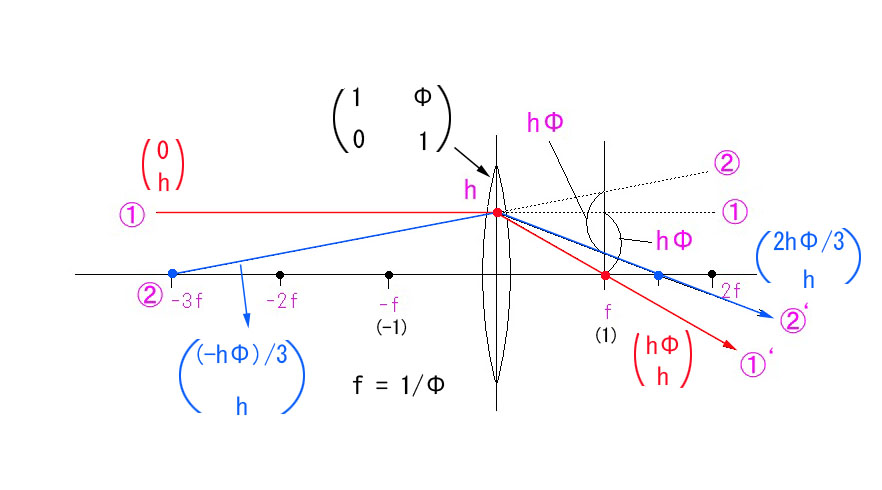
近軸領域では、光線がレンズで屈折するときの屈折角度は、レンズに入射する光線の高さ h とΦに比例します。入射光線の元の傾斜角度を α とすると、屈折後の傾斜角度(←定義された角度)α’ = α+hΦ となります。
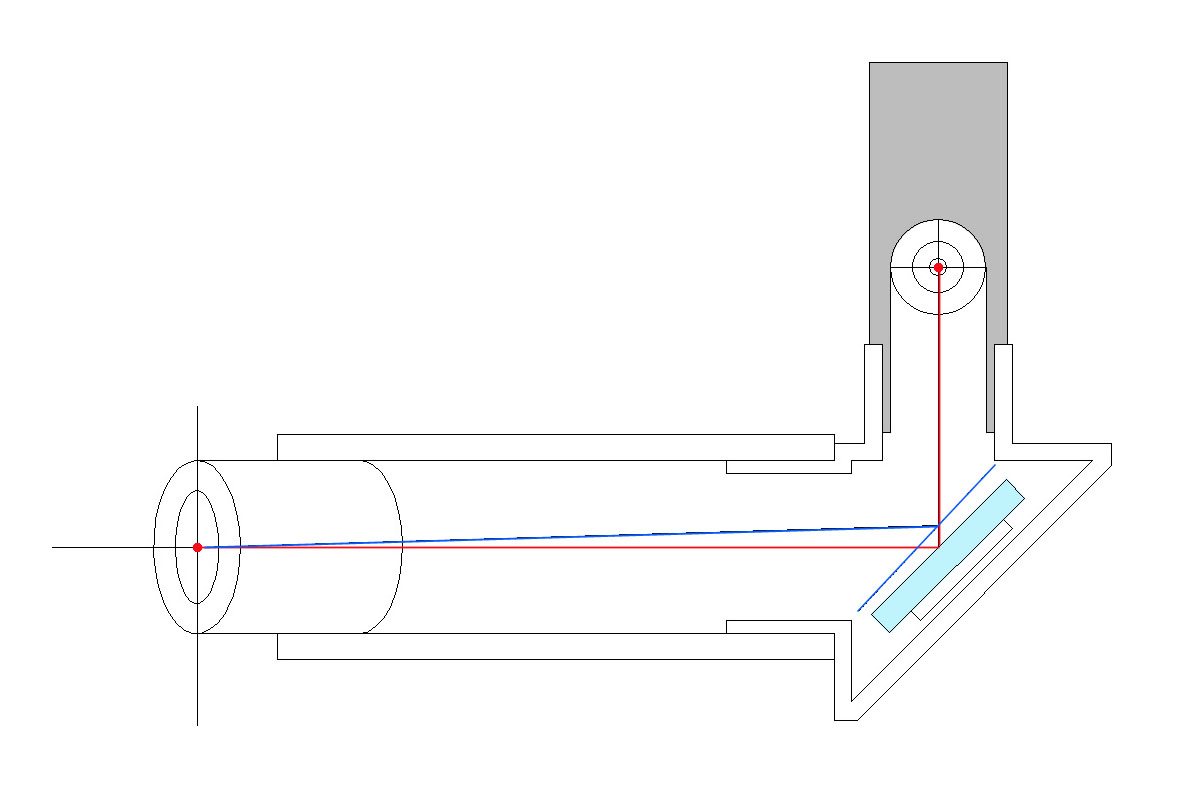
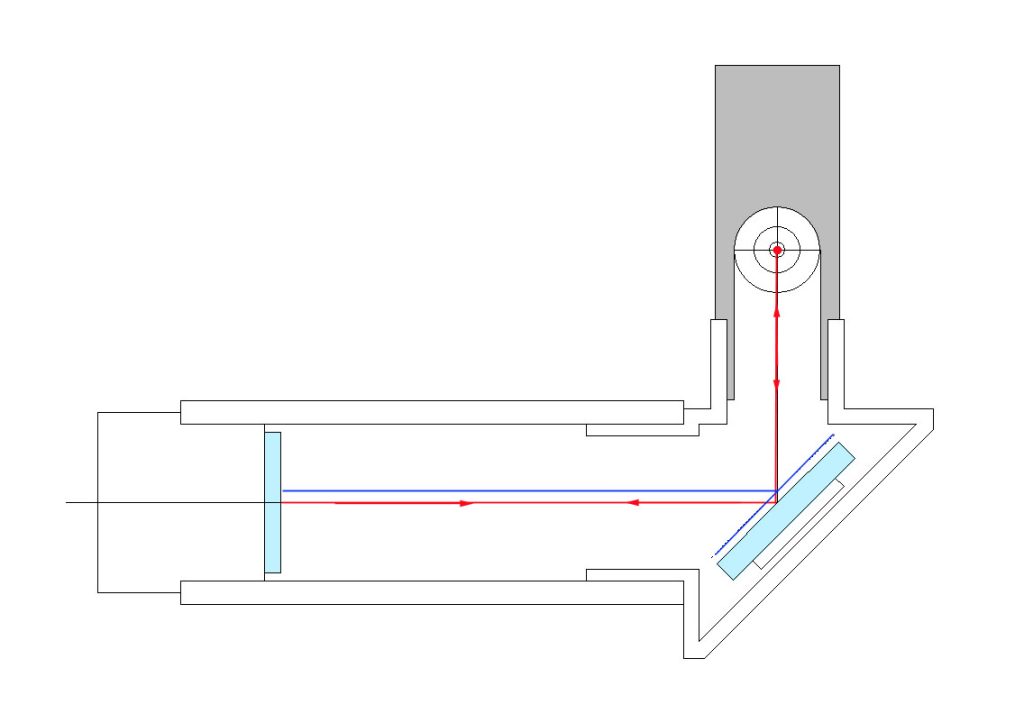
つまり、レンズを通過する都度、傾斜角度が+hΦずつ加算される、ということです。Φ>0であれば、左から右に進む光線は、下向きの角度 hΦ ずつ曲がる、ということです。
赤い光線も、青い光線も、同じ角度だけ曲がる、ということになります。
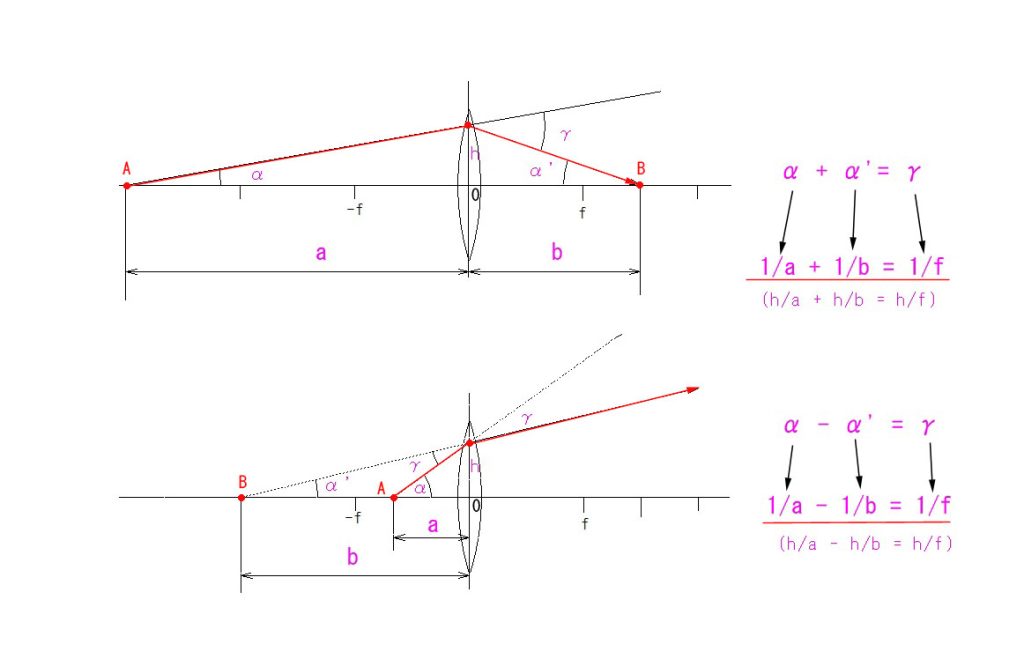
もともと、近軸という特殊な条件で、” h/距離 ” で定義された傾斜角度 α なので、h/α から距離が逆算できるわけです。
入射光線②のような傾き α<0 とし、①のように光軸に平行な入射光線の傾き α =0 とします。
また、屈折光線①’や②’のように下向きに傾いた α >0 とします。
距離の正負の定義から、自ずと傾斜角の正負も決まります。
今一度、整理しますと・・、
*複数のレンズを密着して重ねた場合、合成度数は、単純に各々のレンズのΦ(度数)を合計したものになります。
レンズに間隔がある場合は、
平行光線が最初のレンズに到達する高さ=1として、その光線が各レンズを通過する高さとそのレンズのΦを掛けたものを、繰り返しレンズ枚数だけ加算したものが合成度数になるわけです。
どちらのケースも、ほぼ単純な足し算に帰結するわけです。2行2列の行列が利用できる所以です。