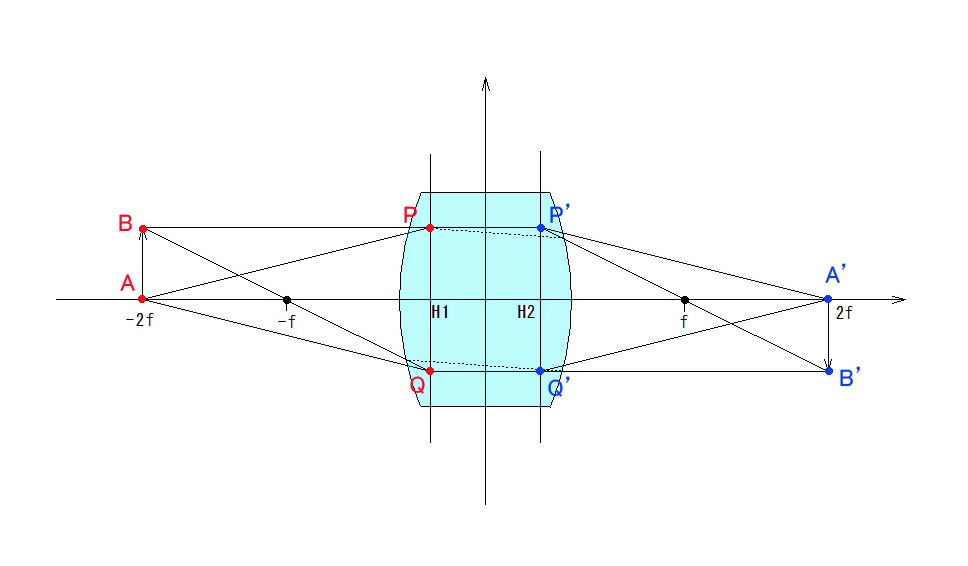
私も当初は、主点の意味が分からずに悶絶した経験があります。しかし、分かれば簡単な話でした。
AB→の像がA’B’→になることは、すぐにご納得いただけると思います。
しかし、Pの像がP’になる、と言われたらどうでしょう？多分、かなりの抵抗を感じられるはずです。
　AからA’、あるいはBからB’に至る光線が、本来の物と像の結像関係とは別に、もう一組の結像関係を秘めているのです。A～Bまでの無数の物点についても同じです。
　Pに収斂する光線の束は、全てP’から発散するように射出する、ということです。
実際には光線はPもP’も通りませんけどね。
　これを文章で表すと、「主点（複数）とは、横倍率＝＋1 の共役点の組。」ということになるわけです。また、主点を通って光軸に垂直な面を、主面と言い、横倍率＝＋1 の共役面、というわけです。
　因みに、図の物と像の関係は、横倍率＝ー1 ですね。

　厚さが無視できない厚いレンズや、複数レンズ系の焦点距離を光学台上で測る方法のご提案です。
　主点位置が特定できなくても、レンズを固定して、「物体」と「像が投影されたスクリーン」を動かし、物体 と 像 の大きさの比が 2：1 になった時に物体の位置を記録し、さらに 物体 と 像 を移動して大きさが 1 : 1 になったとき、「物体」の 移動距離 が 焦点距離 と等しくなります。
　この方法であれば、内部構造が分からない複数レンズ系を非破壊（非分解）で焦点距離を測ることが出来るわけです。

数式アレルギーの方のために、コアな部分を徹底的に可視化してみました。
近軸幾何光学で、お伝えしたいことはこれに尽きます。
　青い角の合計 ＝ 赤い角　です。
　赤い角は、度数 Φ に h を掛けたもの。言い換えると、焦点距離の逆数、1/f に h を掛けたものです。
近軸領域では、入射光線の高さ h が同じなら、赤い角は常に一定だとういことです。

ヒント；　直交するベクトルの内積＝？

　先日、9歳の天才少年が考えたクイズを、親御さんがFACEBOOKに投稿しておられた問題からの、応用問題を作ってみました。＾＾

いろんなアプローチがあると思いますが、出題者の意図は、上図の通りです。
”三角形の一つの角の外角＝他の２つの角の和”；　近軸幾何光学で頻出するんです。