”乱視”も、眼について一般に誤解されているものの代表のようです。
まず、文字面(漢字)のイメージが良くないですね。だから、「あなたには乱視がある!」と指摘されると、大抵、ショックを受けられるようです。
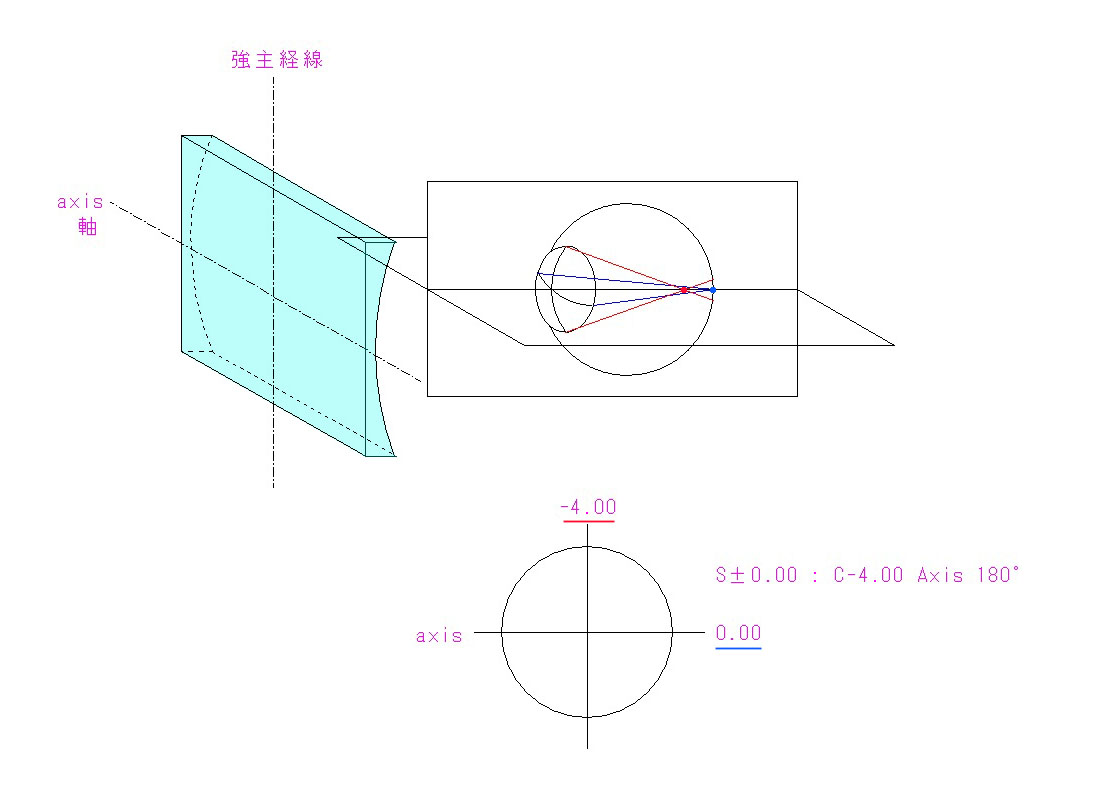
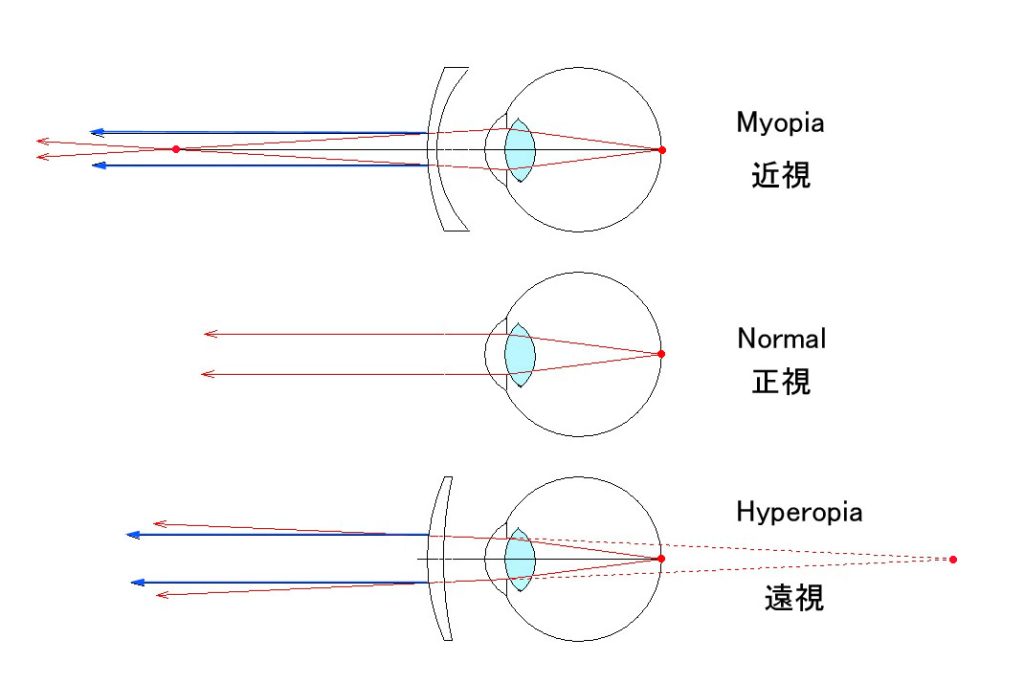
レンズで矯正できる(正規)乱視は、上の図が示すように、眼の経線によって屈折度が異なる眼です。上図では、きっちり垂直断面だけが近視の眼(直乱視)ですが、角度は様々で、検者から見て、右を基点の 0 °~180°まであります。本例は、水平断面が正視の例ですが、水平断面が少し弱い近視だったり、あるいは遠視だったりするわけです。(厳密に測ると、乱視が皆無な人は滅多にいません。)
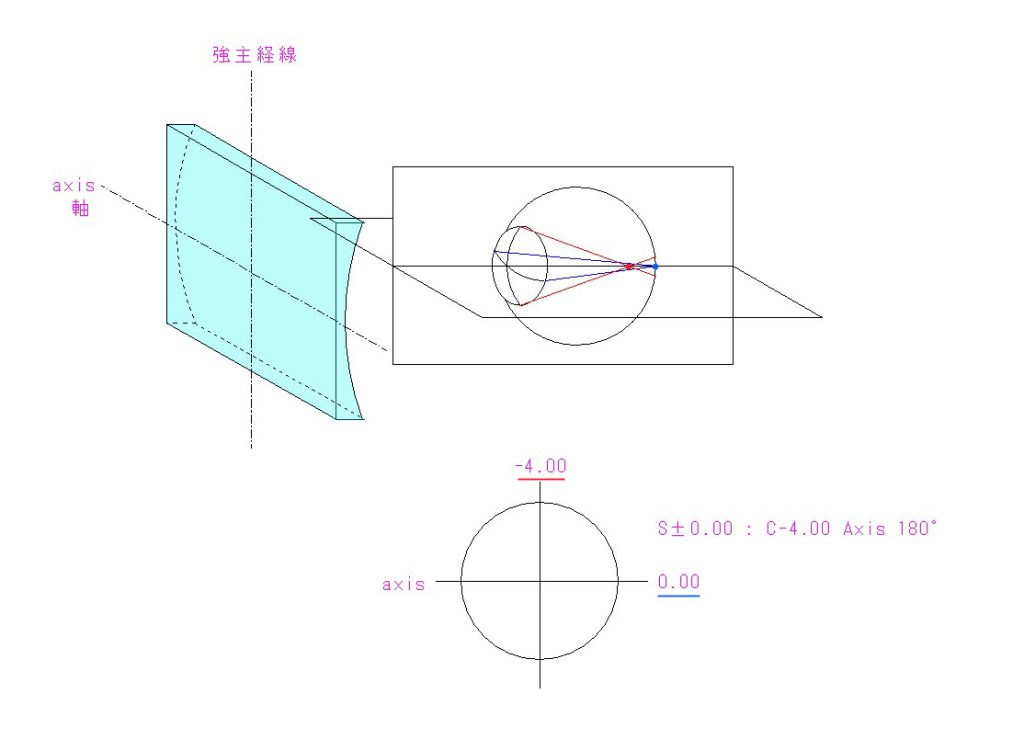
本例の矯正には、図のような円柱状のレンズを用います。分かり易く、文字通り円柱面形状で図示していますが、実際には、メニスカス状に湾曲した、見かけは通常のメガネレンズになります。度がない方向(図では水平方向)を軸と言い、必ず直交した方向が度数最強で、それを強主経線と言います。
本例では、乱視の度数を C-4.00(Cは Cylindrical 円柱の略)としていますが、仮に同じレンズをもう一枚用意して軸を直交させて重ねると、通常のS – 4.00( S はSpherical の略)のレンズと同値になります。
ここで、メガネレンズ表記の約束をご紹介します。
水平方向の度数が -3.00Dで、垂直方向の度数が-4.00Dの眼は、S-3.00 : C-1.00 AX. 180° と表すのが一般的です。理論的には、もう2つの表現方法があります。(AXはAxis, 軸です。)
S-4.00 : C+1.00 AX.90° と、 C-3.00 AX 90°:C-4.00 AX180° です。 どれも理論的には間違いではありません。不慣れな間はピンと来ないかも分かりませんが、少し練習すれば、理解できます。