EMS-UL SET for the C8-BINO completed !
EMS-UL SET for the C8-BINO in the making
Universal Mount for a Binoscope / BINO用汎用マウント
Askar 140-BINO in the making -13; Completed !/ 完成しました。!
EMS-UXL SET for ASKAR185-BINO completed !
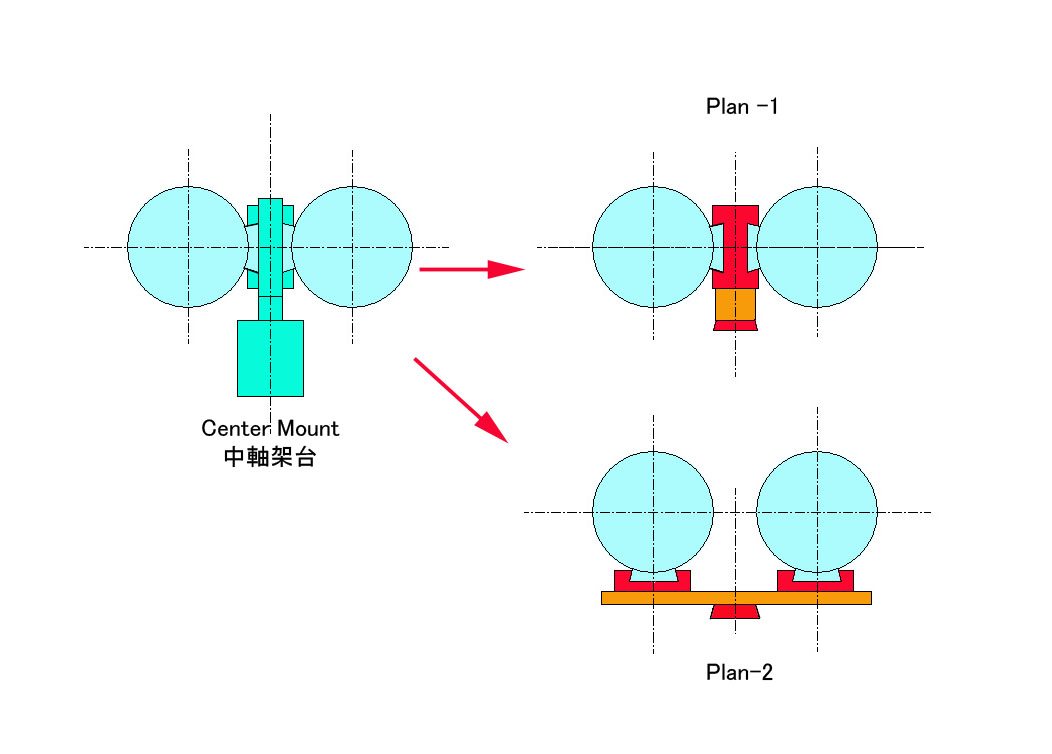
The plans of sharing the different types of the Mount/ 多種類の架台を併用する方法
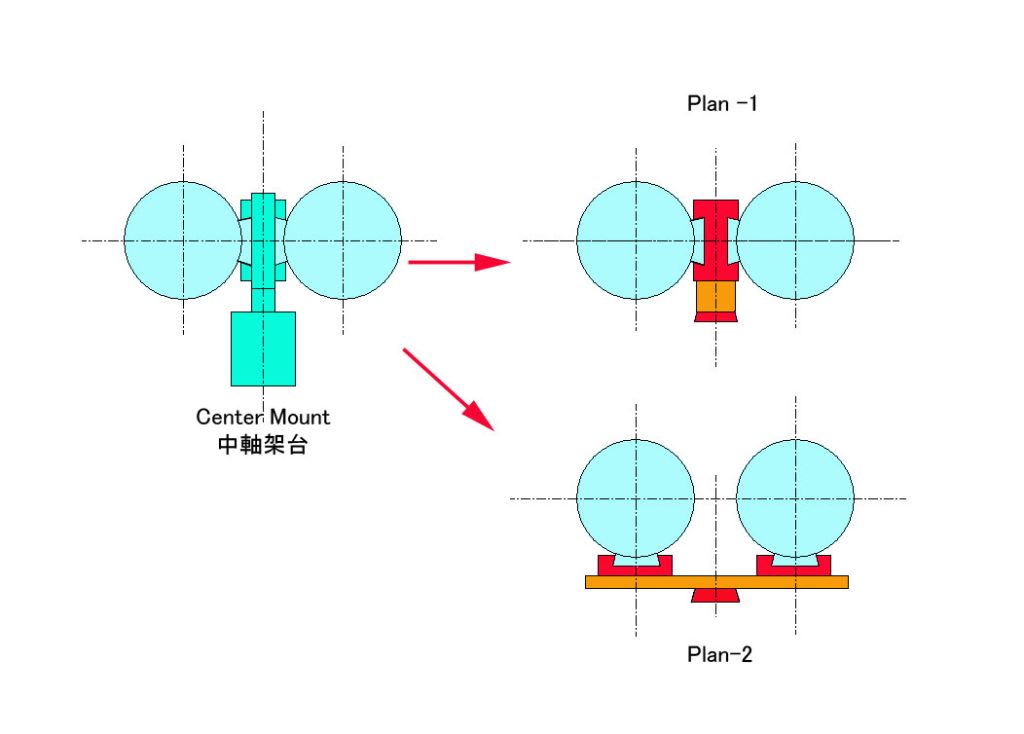
中軸架台(PushTo)を使用している方が、市販の大型GoTo(自動導入)架台との併用を求められるケースが増えて来たので、選択肢をご提案したいと思います。
まず、Plan-1は、中軸架台と鏡筒を全く同じ向きにセットする方法ですが、アリミゾを背中合わせに合体させて、かつ厚みを中軸架台(19mm)と完全に揃えるのは至難であり、また新たに専用のマウントを作るのも大変で、今まではあまり推奨して来ませんでした。しかし、うまく市販パーツを組み合わせると、19mm厚までは行かなくても、それにかなり近い薄さでアリミゾを背中合わせ合体できることが分かりました。
Plan-2は、一番無難な平置き方式です。これだと、鏡筒間隔の設定の自由度が高く、片方のアリミゾをスライド方式にすることも可能になります。たとえば、プライベートな使用では、中軸架台+目幅ヘリコイドで目幅調整をし、多数のゲスト参加を前提とした観望会では、GoTo架台+スライド目幅調整で対応することが出来ます。
現在進行中の物は、15cmF5-BINOのユーザーさんが Plan-1 でGoTo架台を併用されるもので、近日中に工程をUPさせていただく予定です。