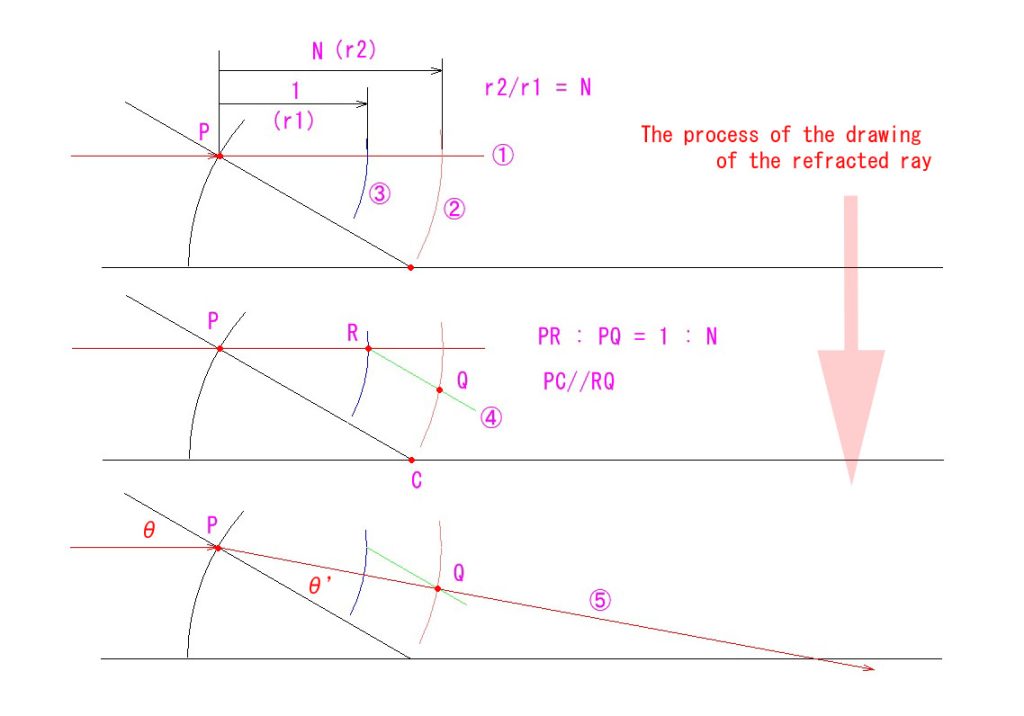
今までで一番難解かも分かりません。分かる範囲でお読み取りください。
せめて、実感を持ちながらお読みいただきたいので、具体的な数値を決めてご説明します。
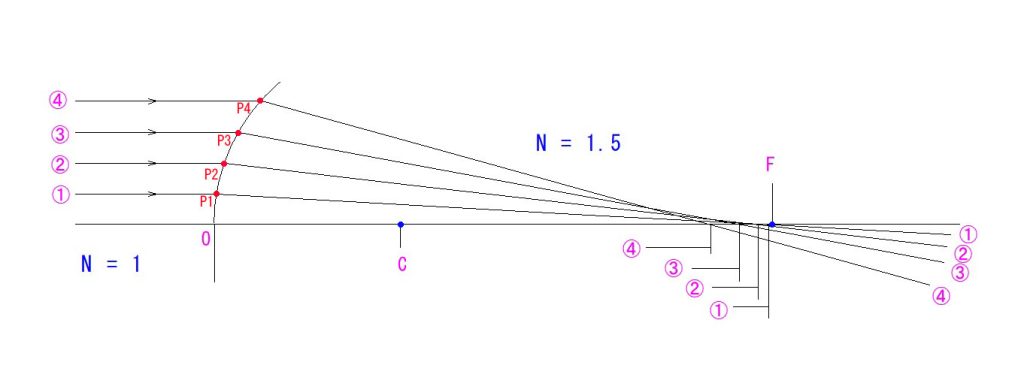
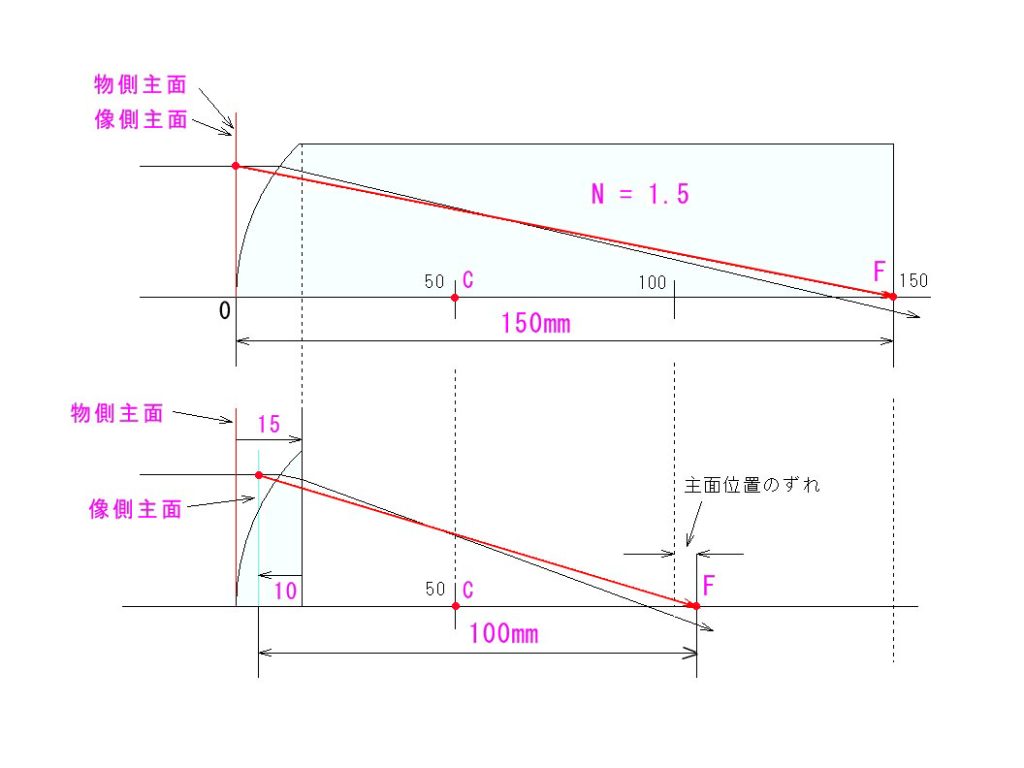
物界は空気中(屈折率1)とします。上の図は、像界が全て屈折率1.5の媒体で満たされているモデルです。界面のr=50mmとすると、近軸の幾何学的焦点距離=150mmとなります。赤い光線が、近軸(理想)結像の直線です。黒い線は、私が実際にモデル上で光線追跡をした実際の光路で、球面収差の影響が出ていますが、これはオマケでお示ししたもので、今回の説明主旨とは無関係です。
幾何学的な焦点距離=150mmと書きましたが、上のように、像界が屈折率N(今回のモデルでは1.5)で満たされている場合、空気中で焦点距離150mmの薄レンズと比べると、像の大きさ=1/Nになります。理由は長くなるので割愛しますが、各自、考えてみてください。
ということは、本例では、上のモデルの150mmの幾何学的焦点距離は、空気中の薄レンズ換算だと、150/1.5=100mmの光学的焦点距離と等価になるわけです。
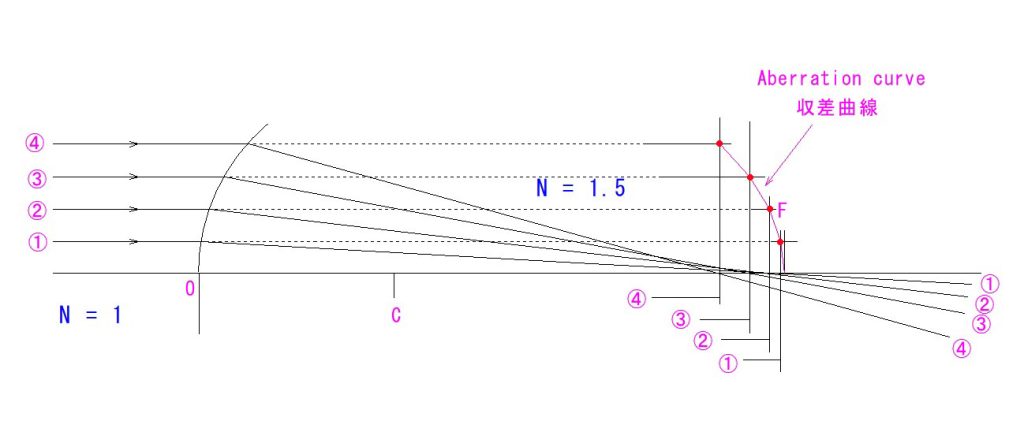
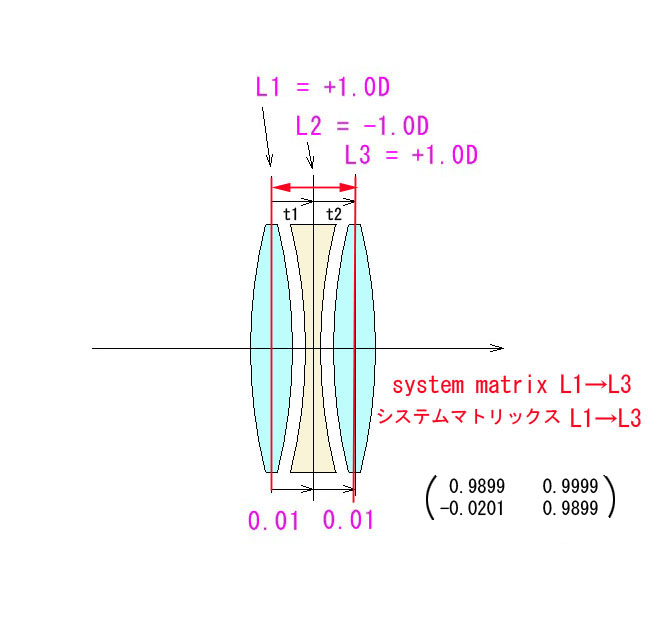
下のモデルは、上のモデルの凸面を厚さ15mmで切り取った状態です。厚み → 0 にすると、両主面が上のモデルに収束して行きます。
この切り取った平凸レンズの焦点距離=100mmです。上のモデルの幾何学的焦点距離を屈折率1.5で割った数値になります。
前回まで、厚み=0 と見なせる薄レンズの近軸光線追跡についての講座でしたが、実際の厚みのある光学系の追跡をどうするか?という時に、最初に必要になる考察をご紹介しました。
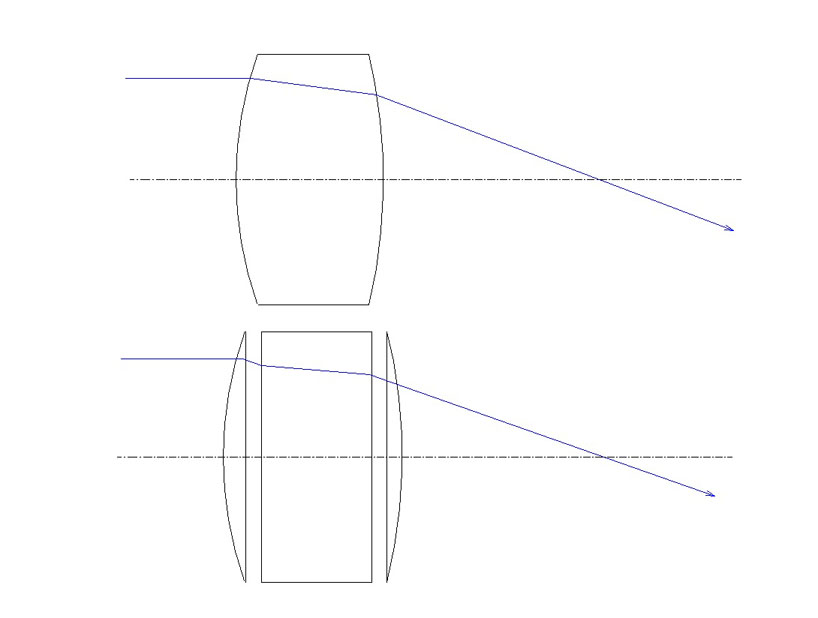
このように、構成する光学面を等価な薄レンズと考え、軸上の厚みや間隔を1/N の等価な空気間隔とみなせば、どんなに厚くて複雑な光学系の近軸追跡も全く障害なく行えるのです。
まとめますと;
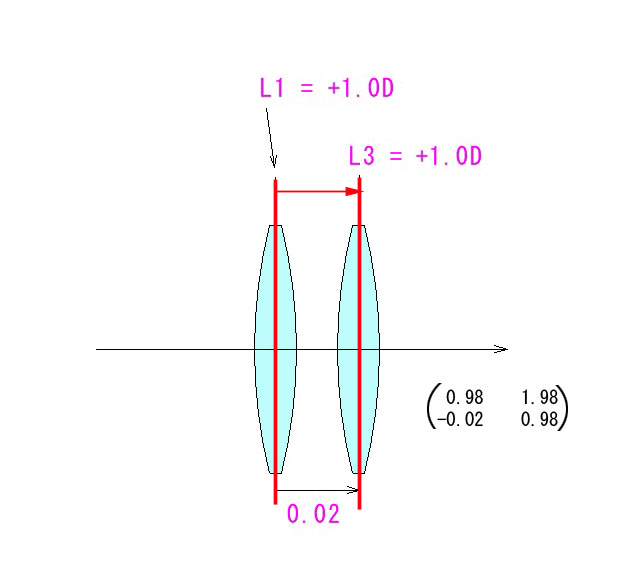
空気中に配列された複数の薄レンズで構成された光学系のシステムマトリックスが、構成するレンズのパワーとレンズ間隔を、代表する屈折マトリックスと移行マトリックスを掛け合わせて行くことで求まる、というのが前回までの講座でした。
それから発展し、屈折境界面を全て等価な薄レンズとみなし、厚みや間隔については、その屈折率で割った換算距離を用いれば、空気中の薄レンズの場合と全く同じ手法が成り立つということです。