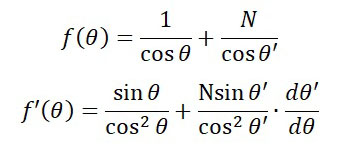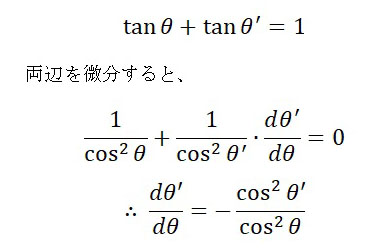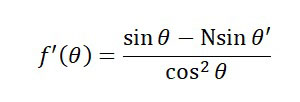
長い解説は読んでいただけないと思うので、簡単にご説明します。
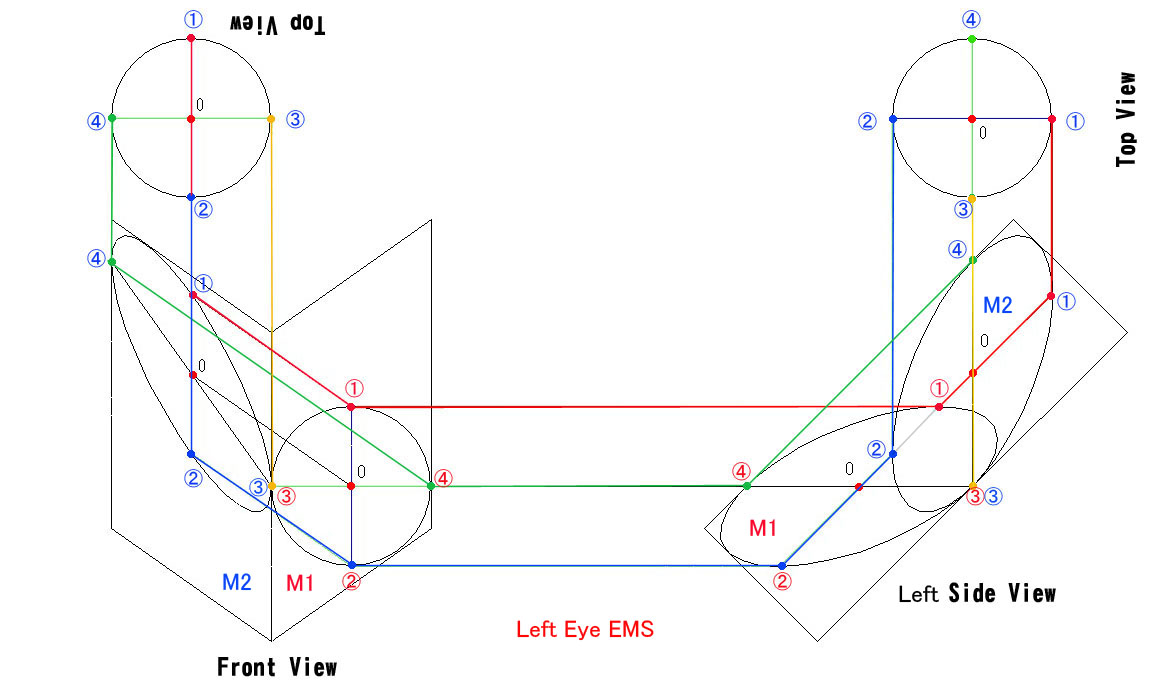
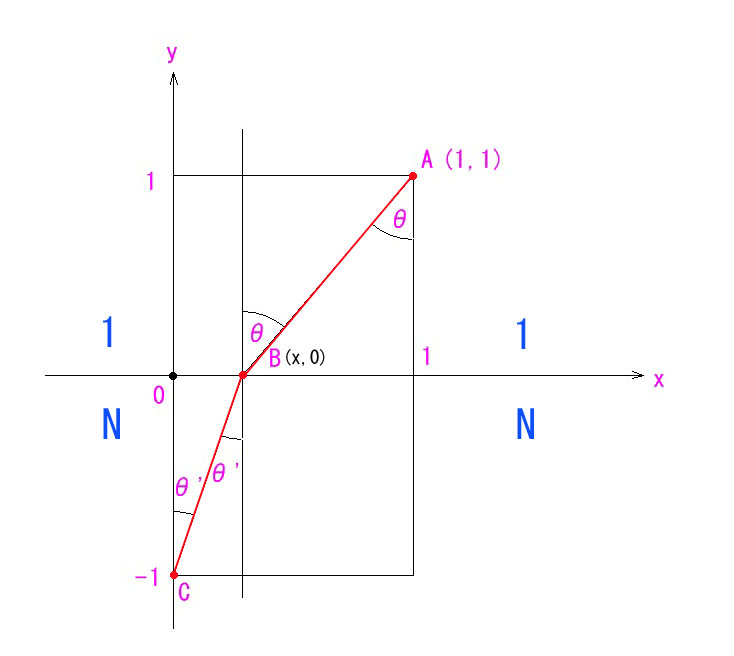
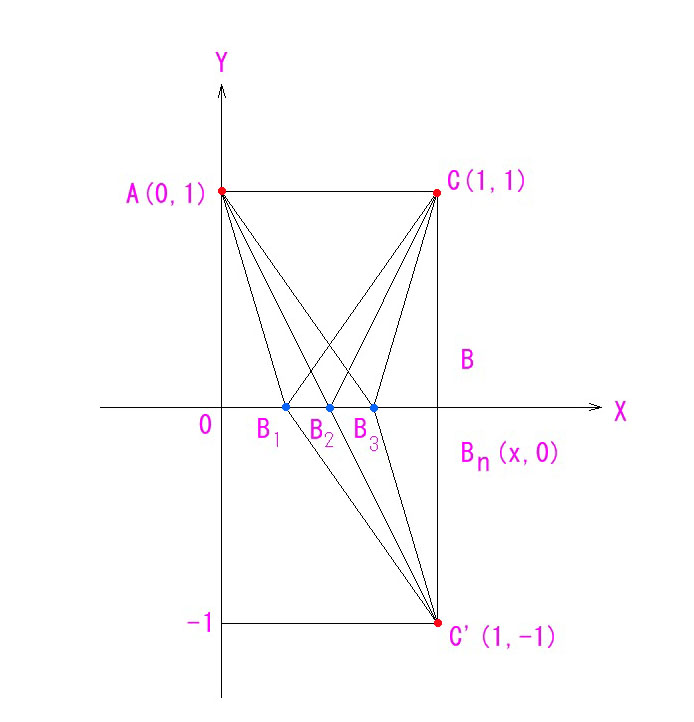
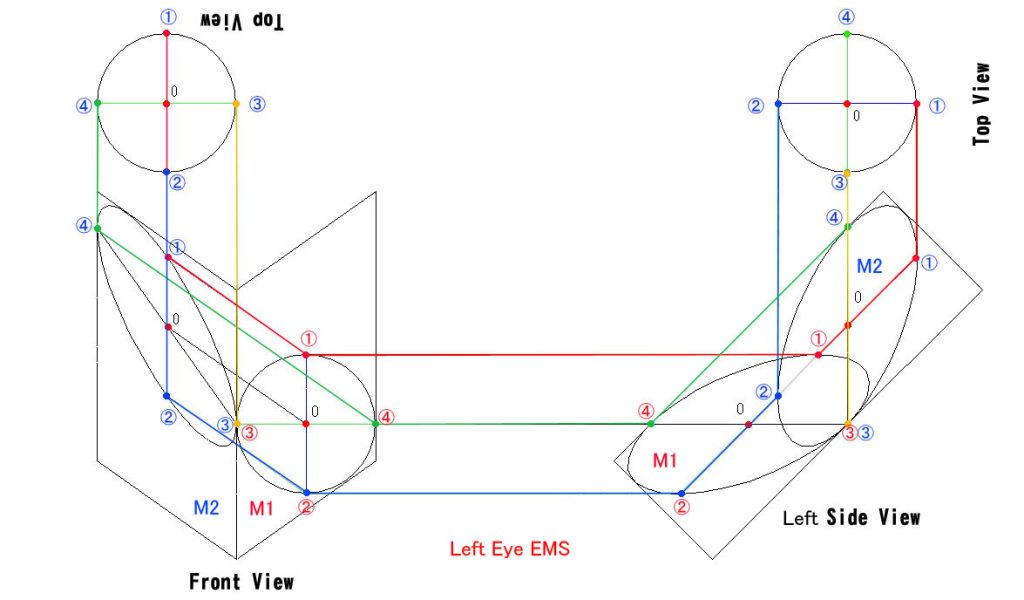
左眼用のEMSの光路の解剖図です。
この図面だけを1年間くらいじっと見ていただくだけでも、いろんなことをご理解いただけるはずです。示唆する物があまりにも多いです。
　立体的に傾斜した光路の画面への投影なので、光線同士が交差しているように見ますが、実際はどれも交差していません。それぞれの光線が最短路を進んでいることが分かります。
　左の Front-View と、右の Left Side-View は完全に分けた方が良かったかも分かりませんが、Front View の開口円（真円）を Left Side-View とで共用させていただきました。
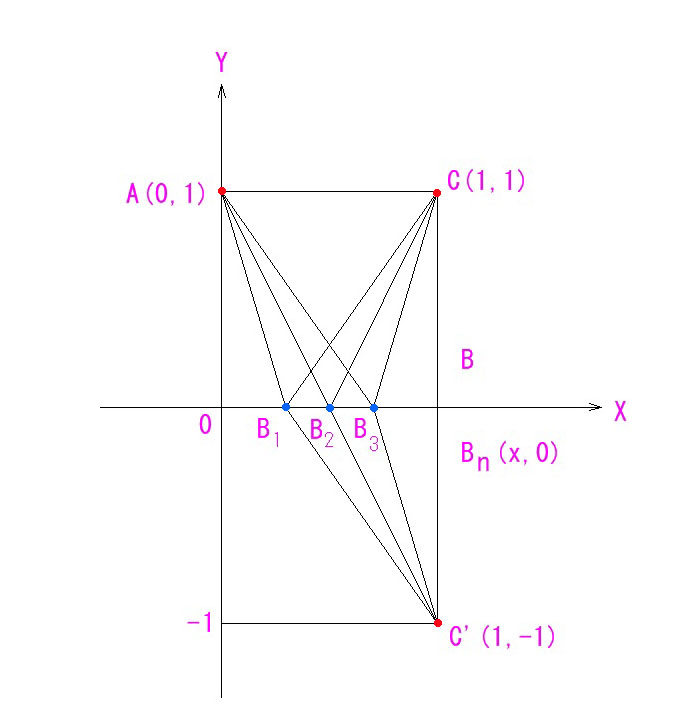
　開口円の ①→①→①→① と、同、②→②→②→② が光路長が等しいことが図面上からも明らかです。
（他の番号も同様（一部空間長を配慮する必要あり））
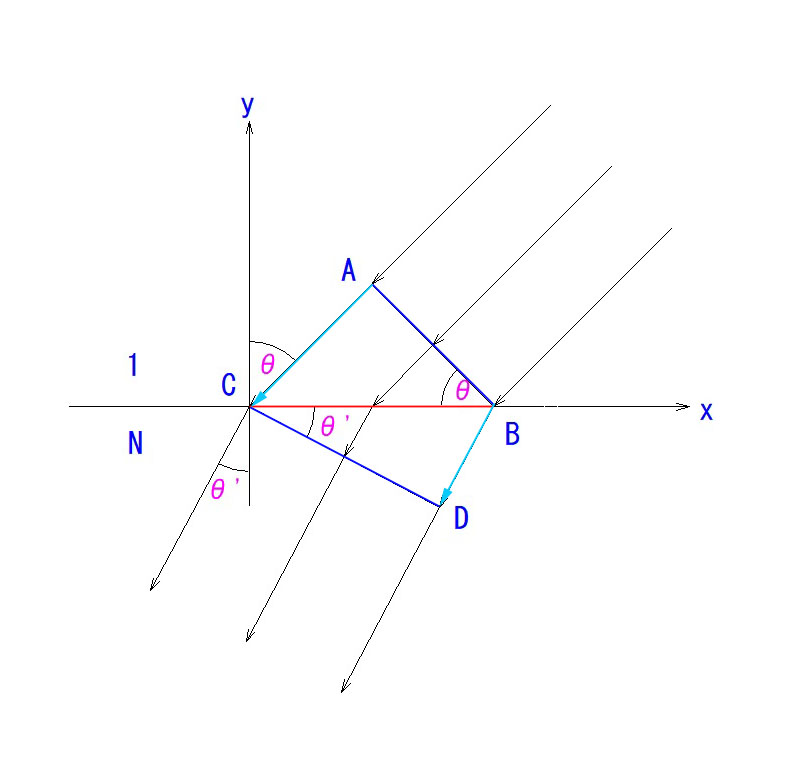
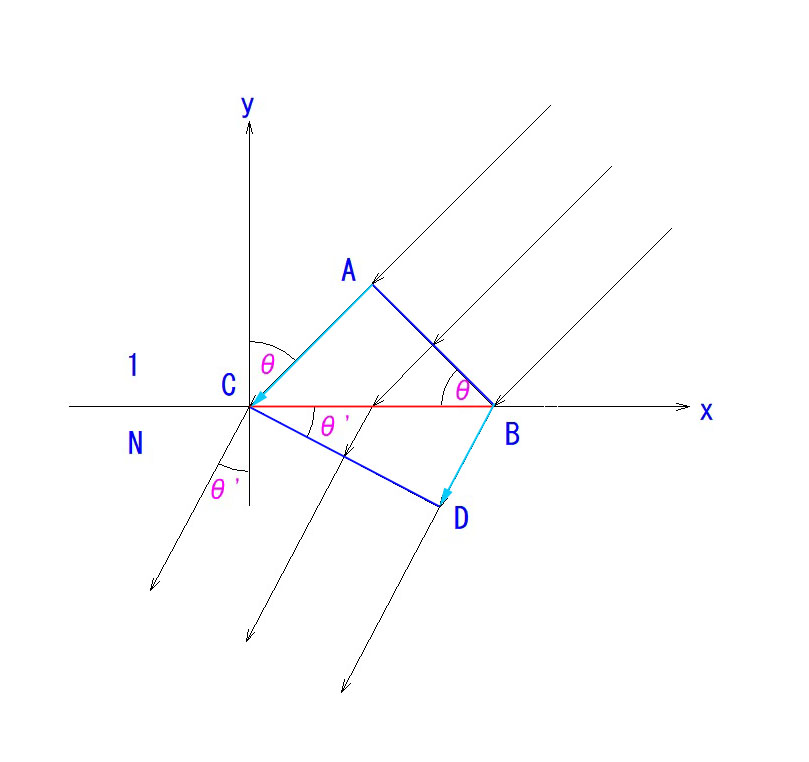
　また、EMSの光線の入射角（面法線と光線の角度）＝60度と、一般の天頂ミラー（入射角45度）よりもずっと反射面との角度が小さいため、開口径に対して非常に長いミラーを要求する点も、EMSの物作りとしてのハードルの高さを物語っています。ミラー同士の干渉を含めて、最大限のミラーを最小限のハウジングに収納するために如何に腐心を重ねた結果であるかをご理解いただけると幸いです。

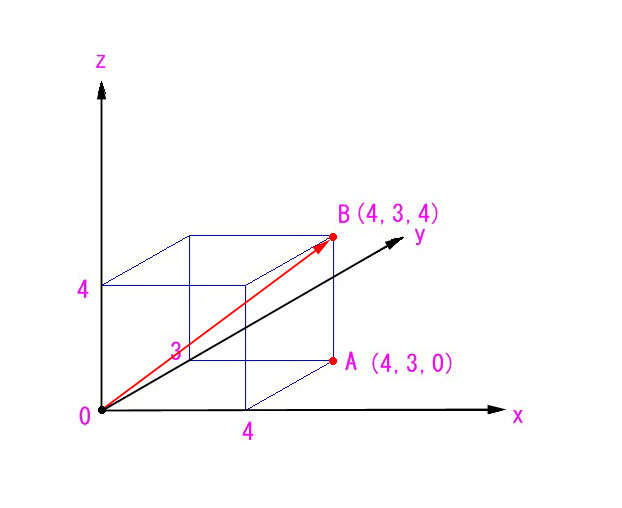
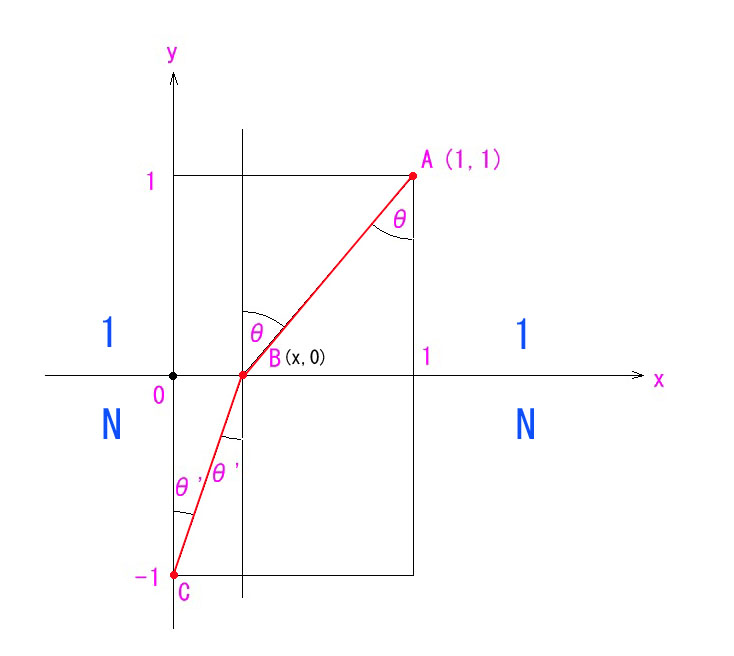
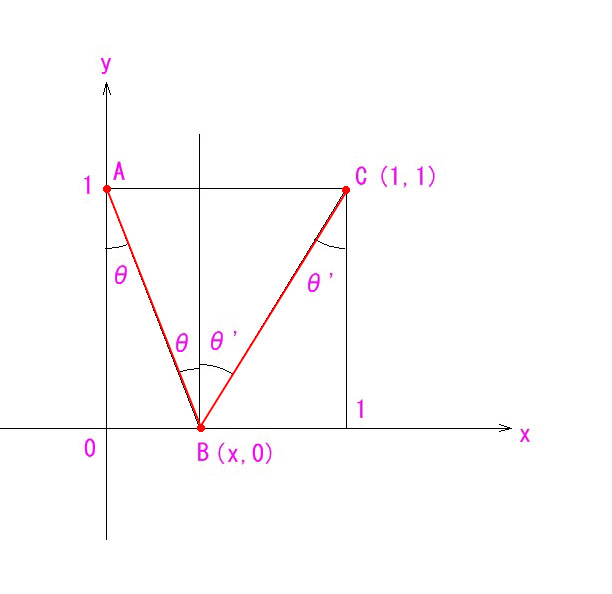
　直感的に理解しにくい課題は、図を描いてみるのがまずお勧めです。また、図が描けるかどうかが、理解しているかどうかの試金石とも言えます。

代数的考察には踏み込まない、と一旦申しましたが、シンプルな方法が閃いたので発表させていただきます。
　まずは、反射の法則から・・・。
　通常は、AB = √(x^2+1) , BC = √｛(1-x)^2+1｝から、f(x)=√(x^2+1)+√｛(1-x)^2+1｝を微分して法則を導き出すのですが、証明したい法則は θ = θ‘ なので、最初から三角関数を用いた方がシンプルになります。
AB + BC = 1/cosθ + 1/cosθ‘ —– f(θ)
　　と、総光路長が非常にシンプルに表せられます。

θ で微分すると、上記のようになります。
dθ’/dθ が邪魔物ですね。
そこで、もう一つの関係式、tanθ + tanθ’ = 1　の両辺を微分してみます。

これで、最初の f'(θ) の式から、dθ’/dθ を消去できます。

　厳密には、これをさらに微分するのですが、今回は割愛して、0＜x＜1 の間に解が一つある前提で進めます。
f'(θ) = 0 のときに、f(θ) が最小値になるので、
　　　　　sinθ = sinθ’ 、すなわち、θ = θ’ が導けました。

屈折の法則も、同様の方法で導けます。

　反射の例との違いは、Y 軸の負領域と正領域で屈折率が違うということです。
上図では、Y 軸の正領域は空気中で屈折率1，負領域の屈折率をNとしています。
光の速度は屈折率に反比例するので、同じ距離でも、Y軸の負領域では、時間がN倍かかるわけです。
Y軸の正領域の速度がN倍、と考えても同じことです。
　従って、最小所要時間の経路を求めるには、Y軸の負領域の光線の長さを最初からＮ倍して考察することになります。
AB + BC = 1/cosθ + N/cosθ‘ —– f(θ)

先程と同様に、f'(θ) = 0 のときに、f(θ) が最小値になるので、
sinθ = Nsinθ’　　が導けました。

　いかがでしょう？　反射と屈折で数式がほとんど同じですね。
以上から、反射面は光線の向きが反転することも考慮して、屈折率＝”-1″の特殊な屈折面として、通常のレンズの追跡方法に一般化出来ることが分かりましたね。

　

　光が最小所要時間の経路を通ることから、所要時間の関数を立てて微分することで、純粋に代数的に屈折の法則を導入できますが、数式を敬遠される傾向が分かったので、今回は純粋に幾何学的、視覚的に納得いただけるモデルを作りました。
　光が光学的密度（屈折率）が異なる界面で屈折する事実—-①、また、平面波（無限遠からの平行光線）の波面（光線に垂直な面）は、屈折前後で崩れない—-② ことも前提として受け入れてください。
さらに、光の進行速度が屈折率に反比例する事実。—③ も認めてください。
　つまり、AC間の光の進行速度は、BD間の N 倍になるということです。
　波面ABがCDに至る時、ACを移動する時間とBDを移動する時間が同じでないと、上の前提が崩れます。
　　これより、
　　sinθ = Nsinθ‘ が確定するわけです。(∵ AC = N･BD)
（ x軸より上が空気の例ですが、両サイドともガラス等（/ 液体）であれば、
　　Nsinθ = N’sinθ‘　）
＊BC=1 と置くと分かりやすいです。