仕事柄、日々眼に関する質問を受けるが、「乱視って、どんな目ですか？」という質問は来ても、近視や正視のことを質問する方はいなかった。酷いのは、「視力0.9以下が近視でしょう？」とか、「遠くが見えないのが近視で、遠くが見えすぎるのが遠視でしょう？」というのもある。
　　視力にからめて理解しようとするのが間違いで、上記の屈折異常と視力は無関係なのです。
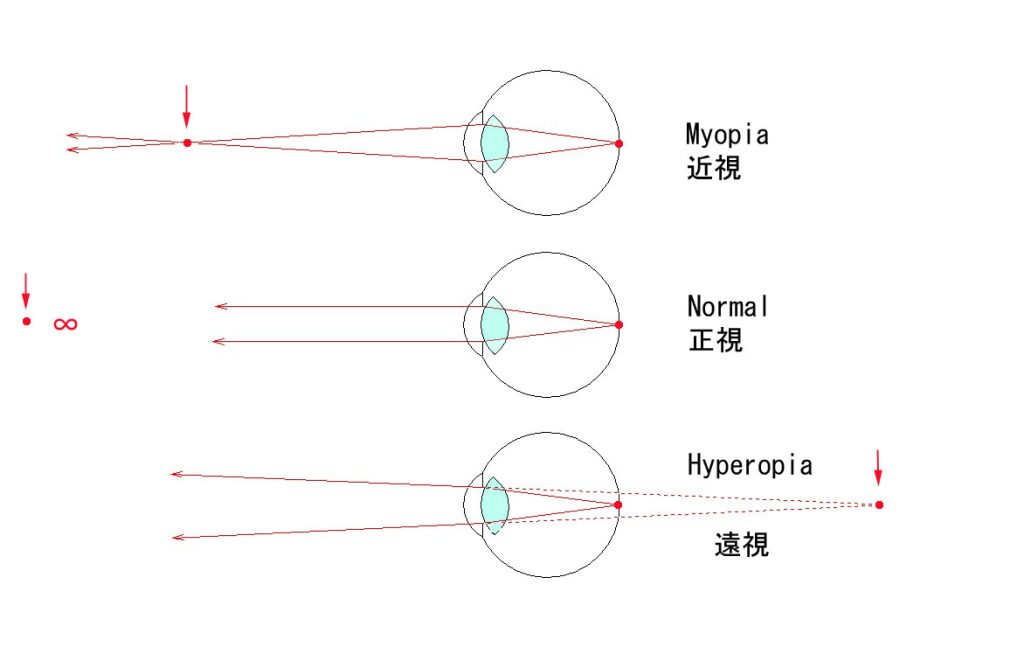
　ちょっと詳しい人は、平行光線が眼底の手前や向こうで結像する屈折異常のモデル図を覚えておられるかも知れませんが、その手の光路図を100年眺めても、屈折異常の定量的な理解には至りません。
　網膜の中心窩（視線の中心）から発して眼外に射出する光束がどこで焦点を結ぶか？を考えることで、矯正するためのレンズ度数が特定できるわけです。若い水晶体は容易に膨らむ（調節する）ので、屈折異常も正視も、全て、水晶体が調節を完全に解除した状態であることが前提です。
　近視は、中心窩から発した光束が眼前の有限距離に結像する眼です。その点のことを遠点と言います。（以下、省略）
　その遠点を焦点とする凹レンズを眼前に装着させれば、その近視は完全矯正できるわけです。

眼底（中心窩）から発した光束は、眼球内の光学エレメント（硝子体、水晶体、房水、角膜）で収斂されて眼外に出るわけですが、近視は屈折力が過剰なために、平行を通り越して余計に収斂して、有限距離に結像してしまうわけです。

眼の屈折異常を視力にからめて理解（誤解）している方にとっては、遠視は難解のようです。しかし、眼底（中心窩）から逆進する光路をイメージすると、明瞭に理解することが出来ます。
　遠視は、さきほどの近視とは逆で、眼の屈折系による収斂力が足りないため、眼の外に出る光束が平行光線になり切らずに、やや発散した光束で出て行くものです。ピントが合わない点では近視と同じなのですが、若い眼は容易に調節して、上の正視に偽装できる（もちろん無意識、自律的に）ため、当人はほぼ自覚せず、周囲にも分からないことが多いわけです。
　近視の場合は、偽装する手立てがない（水晶体は膨れるのが専門）ので、矯正を放置していても疲れることは少ないのですが、割とよく見える遠視の方が、常に偽装しているので疲れることが多いわけです。特に、幼時の遠視を放置するといけないのは、過度の偽装（調節）をする際に、脳が輻輳（より眼にする）の信号を出し、複視を避けるために、効き目でない方の情報を遮断し、いずれその遮断された眼は弱視になって、成長後には復帰しなくなるからです。そうした事例にずっとかかわって来ましたが、それを正確に理解しているご家族はほぼ皆無でした。「何年眼科に通っても、遠視が治らない！」と言われる保護者の方が多くいました。
　遠視のメガネは遠視を治すためではなく、それを放置することによる弱視化を防ぐものなのです。

　まとめますと、屈折異常というのは、遠点が前方（もしくは後方）の無限遠以外にある眼のことです。近視は、眼前の有限距離。　遠視は頭の後ろの有限距離です。頭の後ろに遠点、というのは、初心者には理解し難いかも分かりませんね。眼の眼底より後ろに向かう収斂光線でないと網膜に結像しない眼です。そういう収斂光線は自然界には存在しませんから、無調節では、遠視は遠くも見えず、近くはさらに見にくい眼だと言えます。（若いと偽装（調節）するので、自覚はないのが普通）
　レンズによる矯正は、その遠点の虚像を、眼前のレンズで前方無限遠に作ってやることです。

　”老眼” を屈折異常と混同してはいけませんね。身長と体重を混同するくらいに的が外れています。大人が、体重が2kg増えたから、身長も2cm増えただろう！”と思うくらいの誤解です。

　老眼は、水晶体が十分に膨らまなくなることなので、水晶体が一番薄い状態（無調節状態）での屈折状態を議論する屈折異常とは次元が異なるわけです。

　つまり、正視も、近視も、遠視も老眼になります。近視の方が、「俺はメガネなしで近くがばっちり見える！」と自慢するのは、単なるトリックで、遠方用のメガネを掛けたら、たちまち化けの皮が剥げます。凹レンズである近視メガネを外す行為は、それを打ち消す凸レンズをメガネの上に装用するのと同値だからです。
　遠視の方は、一番悲惨で、遠方矯正用の基本度数の凸レンズに、老眼分の凸を加算しないといけないため、近用メガネは凸＋凸の分厚い凸となるわけです。
　（適当な度数の）近視の方は、基本の凹レンズの上に凸レンズを加算する考え方なので、見かけ上打ち消されて0（ゼロ）度数で近くが快適に見えることが多いわけです。

　

　　準備運動ばかりやっている間に、桟敷席がほぼ空になってしまったことを実感しています。今回は、ご理解いただくというよりも、天文マニアが日々体験しておられて、感心があるはずの事象についてご説明します。意義が分かれば、基礎から理解しようとするモチベーションも高まるかと思うからです。
　望遠鏡を地上目標に向けた時、近い目標ほどピントが外（手前）に出て来る現象は、天文マニアなら、もはや空気を吸うように、日々実感しておられるはずです。
　「自室の窓からはせいぜい100ｍくらいまでの目標しか見られないが、無限遠の対象でのピント位置との差を把握したい。」
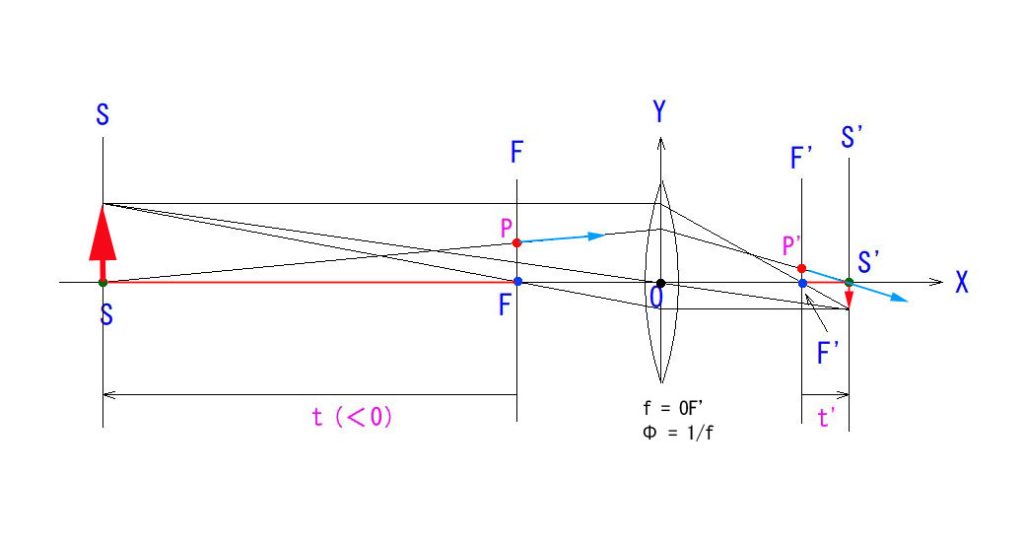
　↑こんなご経験が何度かあったはずです。バックフォーカスがシビアな場合には、これは深刻な問題となりますね。上図で言うと、t’ が知りたいわけです。　具体例として、焦点距離1ｍで、目標距離 (t+1)が101mのとき、t’ = 0.01m =1cmとなります。

　レンズを基点にした結像公式 　(1/s’ – 1/s = 1/f ) 　は皆さんよくご存じかと思いますが、２つの焦点（F,F’;物側、像側）を基点にした結像公式（ニュートンの公式）もあります。
上図によると、
( t･t’ = – f^2 )　というのが、ニュートンの結像公式です。右辺に( – )が付いているのは、t＜0とする約束のためです。（絶対値だけ問題にするのであれば、( – )は省いても良いでしょう。）
ニュートンの公式は、一般的な結像公式 (1/s’ – 1/s = 1/f ) に s’= f + t’； s= -f + t を代入して整理すれば得られますが、計算に慣れていない方は面倒かも分かりません。
　では、２つの焦点(F,F’)面を基点にした 焦点マトリックス と、物体面と像面 (S,S’) を基点にした 物像マトリックス を求めてみましょう。

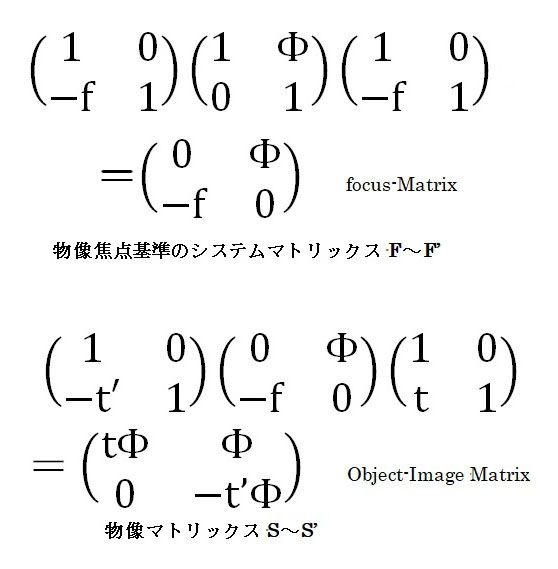
焦点基準(F-F’)のマトリックスからでもニュートンの公式は簡単に導出できますが、下の物像マトリックスではより簡単に導出できます。
以前にも、申しましたように、どんなシステムマトリックスも、行列式の値＝1 ですので、
t ･(-t’)･Φ^2 = 1　→　t ･t’ = -1/ Φ^2 = – f^2　　となります。
　また、物像マトリックスの右下の成分＝横倍率 M で、その対角成分＝1/M となることは以前にもご説明しましたが、これも注目すべき点です。左下の成分＝常に0です。

＊　行列の掛け算は、結合法則｛ A(BC)=(AB)C ｝は成り立ちますが、交換法則は成り立ちません ｛ ABC ≠ CAB ｝ので、ご注意ください。
　それから、左から右に掛けていくという行列の計算の事情から、各屈折や移行を代表する要素行列の並び順が実際の光線の進行方向とは逆になります。
　言い換えますと、光線は 左 → 右 ですが、、該当する要素行列は 右 → 左、と、全く逆の並びになりますので、混乱しないようにお願いします。

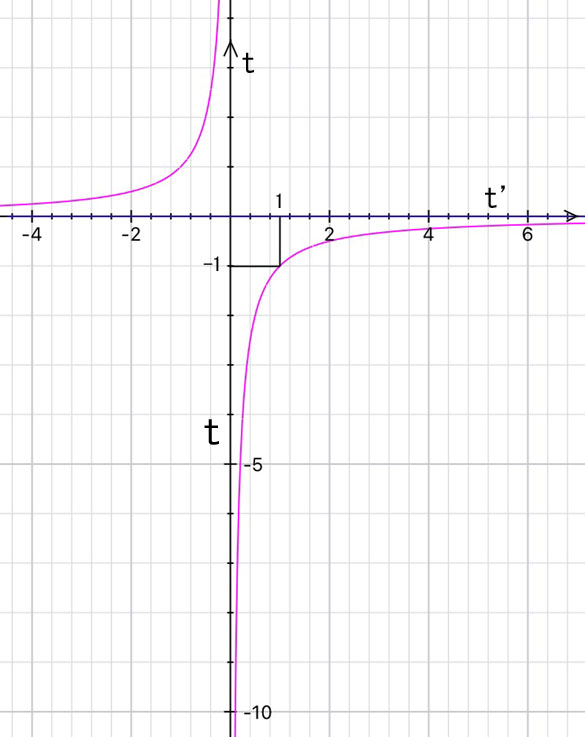
　最後に、t,t’ の関係を、焦点距離1ｍとして、グラフにしてみました。目盛りの単位＝1mです。
原点（座標軸交点）が焦点になります。ただし、t’ 軸については、一般的な焦点（像側）であり、t 軸については、物側焦点となるので、同じ原点であっても全く異なる点を基点としています。”ニュートンの公式”の最初の図を参照しながら見ていただくと、理解しやすいかと思います。

　左上（第2象限）のグラフは、望遠鏡対物ではほぼ使用しない領域です。t＞0ということは、物体が対物レンズの物側焦点より手前（焦点距離1mだと、対物レンズから1ｍ以内）なので、あり得ませんね。しかし、理論的にはあり得るわけで、その領域に入ると倒立実像ではなくて、遠い前方に正立虚像が出来ます。つまり、物体が１ｍ（焦点距離）以内に来ると、対物レンズはルーペになるわけです。

　ということで、天文マニアにとって、関係あるのは、右下（第4象限）のグラフで、しかも、天体望遠鏡で10ｍ以内の目標を見ることはまずないので、切り取ったグラフの枠外、ずっと下側で使うことになります。グラフはもはや曲線というよりも直線に近くなりますね。
　| t |=t’ （本例では1m）となる点がありますね。それぞれが、物側焦点、像側焦点から焦点距離分離れた点に位置するときです。
　ですから、レンズを基点にすると、それからの距離の絶対値が 2f となる点です。
　その時、物と像の大きさが全く同じになります。
　これを応用すれば、未知の光学系の焦点距離を非破壊（非分解）検査することが出来ます。

上の連立方程式を、行列で表記すると、下の式になります。
このくらいの連立方程式ですと、そのまま暗算でも出来ますが、行列を使用するメリットは、計り知れないものがあります。
　2行2列までの行列の演算はすぐに覚えられますので、どうか毛嫌いしないで、昔の教科書を引っ張りだすなり、ネットで検索するなりして、復習してください。

近軸光線の屈折について、基礎からご説明します。
近軸とは、光軸に極限まで近付いた光線のことで、理想的な結像をすることは経験的にも分かっていますが、そのままでは作図も考察も出来ないため、常に高さ(h)のある光線を想定することになります。
　言い換えますと、近軸光線追跡は、完全無収差の光学系による理想結像をシミュレートするものです。

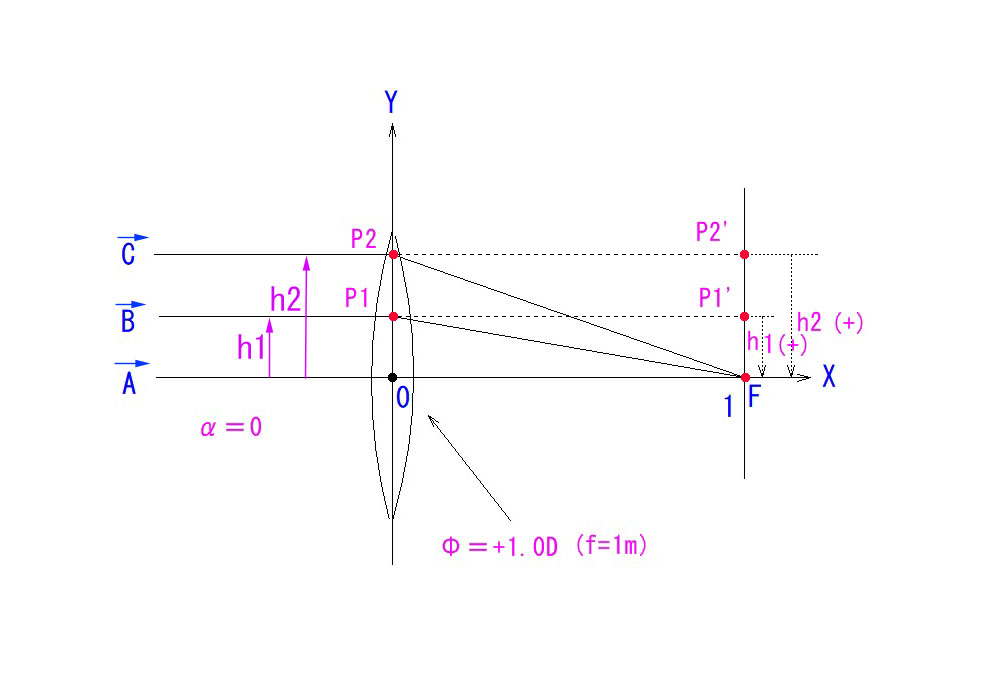
　上図のように、平行光線 A, B, C が全て F に結像するのが、理想結像です。
今回も、レンズは厚みが無視できる、度数Φ＝+1.0（焦点距離＝1.0m）の凸レンズとします。
Φ＝1.0Dとしたのは、光線傾角 tangent の分母が常に１になり、傾角要素のαが、α＝tanα＝h となって、長さの要素として可視化できるためです。（αは、下向きが＋で、上向きがーです。）

　入射光線の傾角 α について、パワーΦの屈折面を高さ h で通過後に α’ となるとすると、
α’＝α＋hΦ　（Φはレンズの度数、1/f ）　となることについて、図に則してご説明します。
P2で光軸に平行に入射する光線 C は、傾角α＝0，h=h2, Φ=1, を、それぞれ上式に代入すると、
α’＝0+h2 = h2　となり、焦点 F でX軸と交わります。
光線 B も同様に計算できます。（α’＝h1）

　光線は、屈折点Pで、レンズの度数と、光軸からの屈折点の高さに比例した角度で折れ曲がるということです。（α＝tanα で定義された屈折角度）　上例は、入射角 α＝0ですが、α の値とは無関係に、屈折面に突入する高さｈでの光線の折曲がり角度（α＝tanα で定義された屈折角度）は一定なのです。

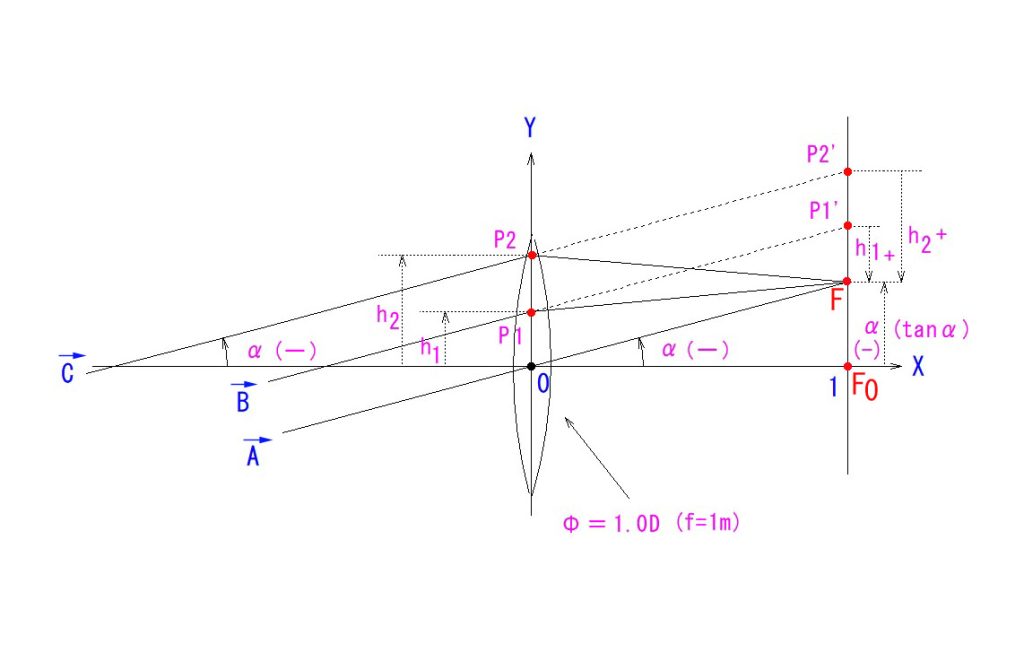
　先ほどは、入射角 α＝0 の特殊なモデルでご紹介しましたが、上図のようなケースも、全く同様にご説明できます。

　入射光線 B についてご説明しますと、P1で屈折しない場合は、P1’に到達しますが、屈折により、P1’→Fに移動するわけです。
　お気付きと思いますが、αもα’も、通常の角度ではなく、tanα で定義されているところが重要です。
この図でも、α’＝α＋hΦ となっていることがお分かりになると思います。

　理想の薄レンズに入射する光線は、「レンズ上の入射点の高さ h とレンズの度数 Φ に比例した角度で曲がり、それは入射光線の傾角に依存しない。」—ということです。（ただし、角度は下向き “tangent”で定義された値。）
*　h の初期値には、全く制限がなく、どんな数字を入れてもかまいません。（計算に好都合な初期値で良い）; 　

繰り返しになりますが、
　　α’＝α+hΦ
　　h’= h
これを行列表記すると、こうなります。↓

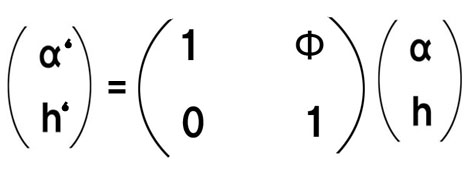
また、2つの屈折面に挟まれた空間は屈折せずに直進するため、αは変化せず、h のみが変化します。
通過間隔（光の進行方向＝＋）＝ t とすると、
α’＝α
h’＝ h – αt
これを行列で表記すると、こうなります。

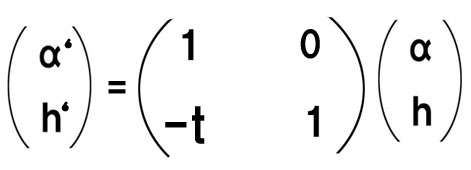
　どんなに複雑に見える光学系も、屈折マトリックスと移行マトリックスを次々に掛け合わせることで、その全系のシステムマトリックスが得られるわけです。結果として得られたシステムマトリックスの行列式の値も1です。

＊一見、通常の平面上の幾何学的ベクトルと混同し勝ちですが、そうではありません。
　　α、α’はｘ座標ではなく、その光線の基点に於ける傾角（特別に定義された）です。

また、準備運動しましょう。
　光線をその位置に於ける傾角と高さで表すと、非常に便利ですよ、というのが前回の講座でした。
では、実例に則して、概略をご説明しましょう。
レンズは、厚さが無視できる、焦点距離１ｍ（度数＝1.0Ｄ）の凸レンズとします。
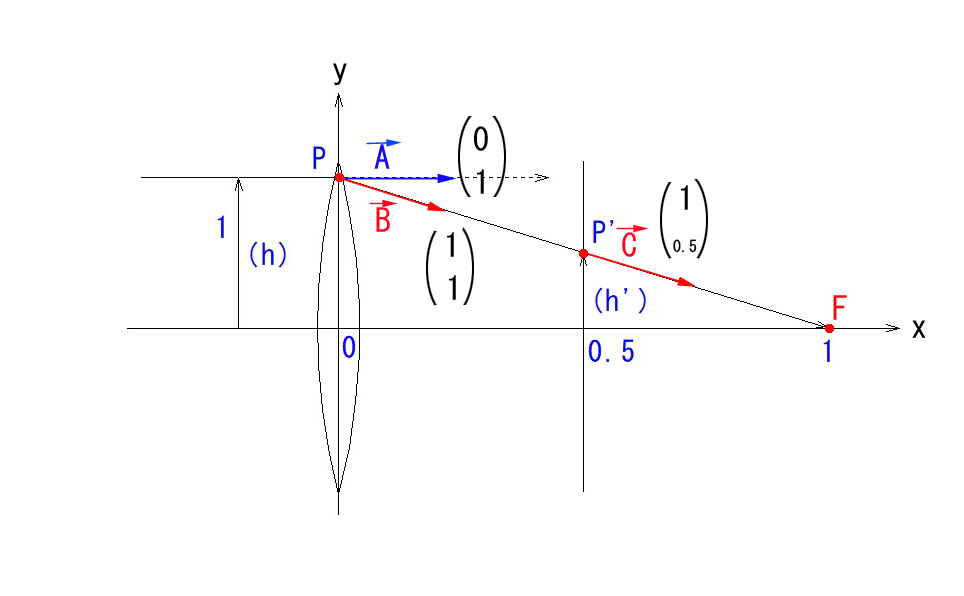
　まず、X軸とＹ軸の尺度が違うことに気付かれたと思います。この辺も初心者にはハードルになりますが、近軸光線追跡に用いるXY座標は、X,Yの尺度を統一する必要がないのです。理由を話すと長くなるので、今回は詳細は割愛しますが、一般的な結像公式(1/S’-1/S=Φ)の両辺にhを掛けたことと同じですので、問題ないわけで、これが、この方法の強みなのです。

　次に、P点での光線ベクトルが２つあるのにも違和感を覚えられたかも知れません。
屈折面では、瞬時に光線の方向が変わるため、同じ点に屈折前(A→)と屈折後(B→)の、２種類の光線ベクトルが存在するわけです。前回、位置ベクトルではない、と申し上げた所以です。
　光線の進行を最初から辿ってみます。

1.　入射光線は、Y軸に一致した屈折面に、光軸に平行に、高さ 1 で突入します。
　　横に、α（傾角）とh（高さ）を成分とする 行列 A→を併記しました。
2. 　光線は、同じ位置のまま、屈折して、光線ベクトル B→ に変化します。
　　　これも、行列B→を併記しています。
3.　この光線追跡方法の有用なところは、基準面をどこにでも設定できることです。
　　練習のために、レンズと焦点の中間点(X=0.5）に新たな基準面を立ててみました。
　　光線がPに到達した時、傾角は元のままですが、高さ(h)だけが半分になります。
　　　これも 行列 C→ を併記しています。

　今回は、（逃げられないように^^;）敢えて計算式を省きましたが、Ｐ 点では、レンズの 屈折マトリックス、P’では、X=0→0.5 の間の 移行マトリックス を掛けてやることで、新たな α と h が決定できるということです。
　屈折マトリックス、移行マトリックス について、改めてご興味を抱いていただけましたら、講座の最初から見直していただけると幸いです。

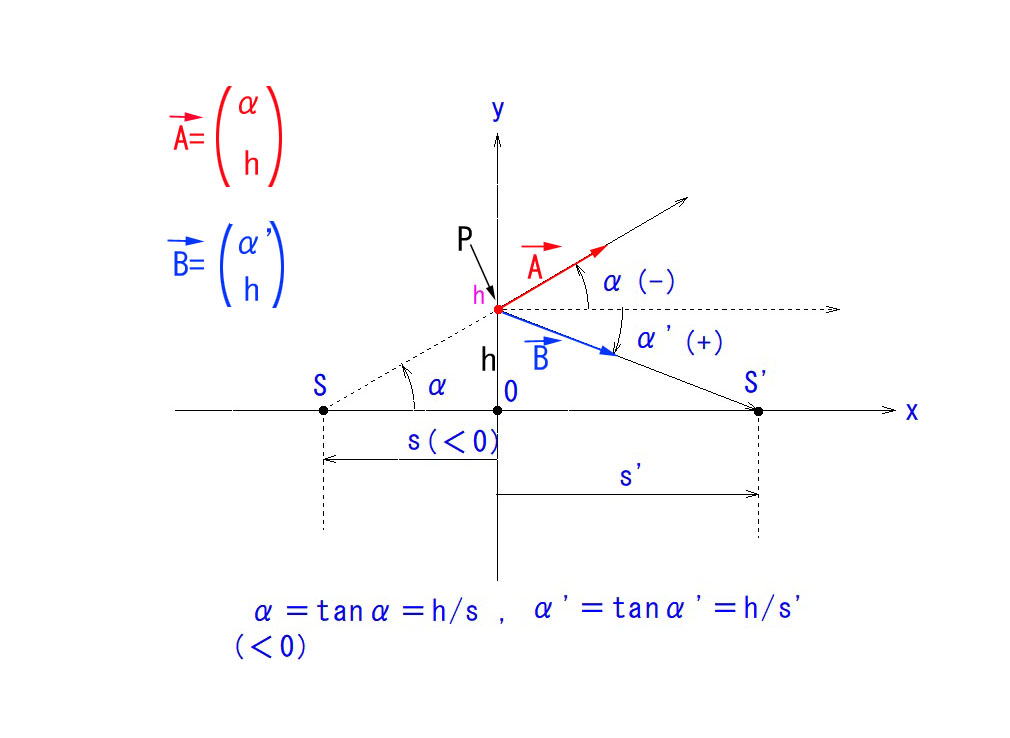
　光線の傾角の定義や、物点/像点 の位置の正負の約束を講座の最初にしっかりとご説明すべきでした。
後先になりましたが、改めてご説明します。まず、図から、角度の正負の方向の定義をご確認ください。

　上図は、必ずしも物点Sと像点Sをお示ししたのではなく（そう解釈されても問題ありませんが）、光線が（進行方向に対して）上向き傾斜のベクトルAと、下向きのベクトルBに分けてご説明するものです。
　S,S’が物点と像点だとすると、1/s’ – 1/s = 1/f から、3つのパラメーターの一つが分からなくても、その値が求められることはご承知の通りです。
　今回の一連の講座は、一般的な結像公式を使わずに、光軸に垂直な基準面（線）上の（光軸からの）高さｈの点を通る光線を、傾斜角αとhとの2元のベクトルで表し、屈折面と面間隔の通過による変化を追跡する方法をご紹介したものでした。
　ただ、二次元平面上のベクトルと言うと、どうしてもXY座標中の位置ベクトルを想起されると思いますが、それとは異なります。この辺が混乱を招くのでは？と心配しております。
　図中の2元ベクトル、A,Bの成分の下の方は、点PのＹ座標なので、問題ないと思いますが、上の成分はＸ座標ではないことにご注意ください。
　上の成分は、図中で定義した傾角＝α であり、それ自体に方向の情報を持っていますが、tanαというスカラーとしてご理解いただければ良いと思います。

　なぜ、光線の傾角の正方向を、数学の慣例の半時計回りとしなかったか？ですが、ｘ座標の正領域と、実像点の位置の正領域が合致するためには、図の方向を正とすることが必須でした。図のように定義すると、像点の位置の正負とｘｙ座標とが矛盾なく合致します。

Now, I am asking 5-optical common sense quiz.
Each of the answering time-limit is 20-second.
光学常識問題を５つご用意しました。制限時間は、いずれも20秒です。

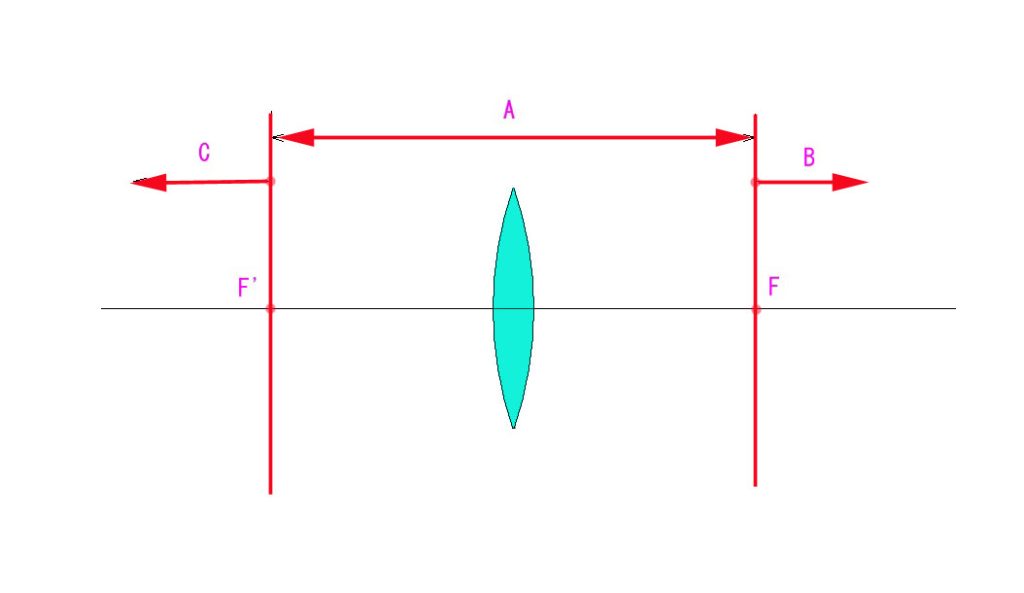
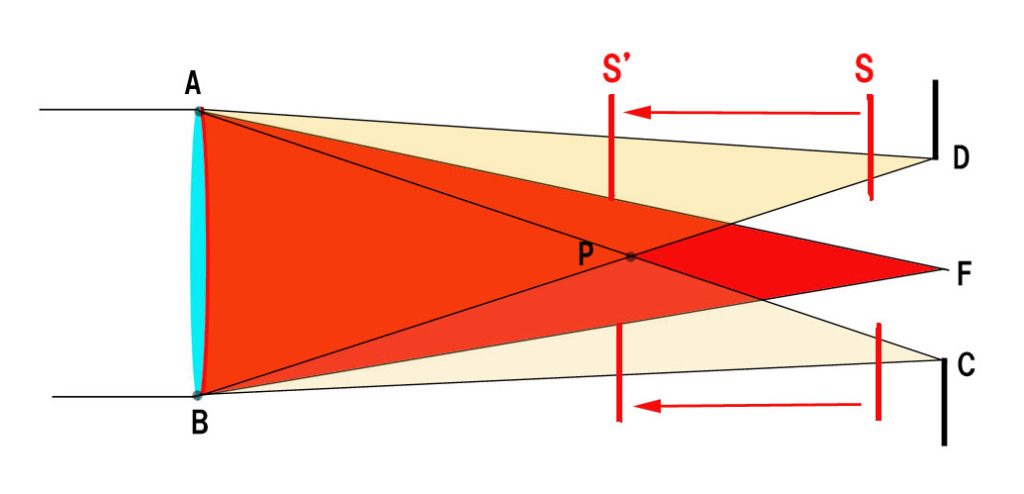
Q2; Which is the area that will not allow the real image of the real object?
実物点の実像が出来ない範囲は 1～3 のどれ？
　　1. A, 2.B & C, 3. nothing （該当なし）

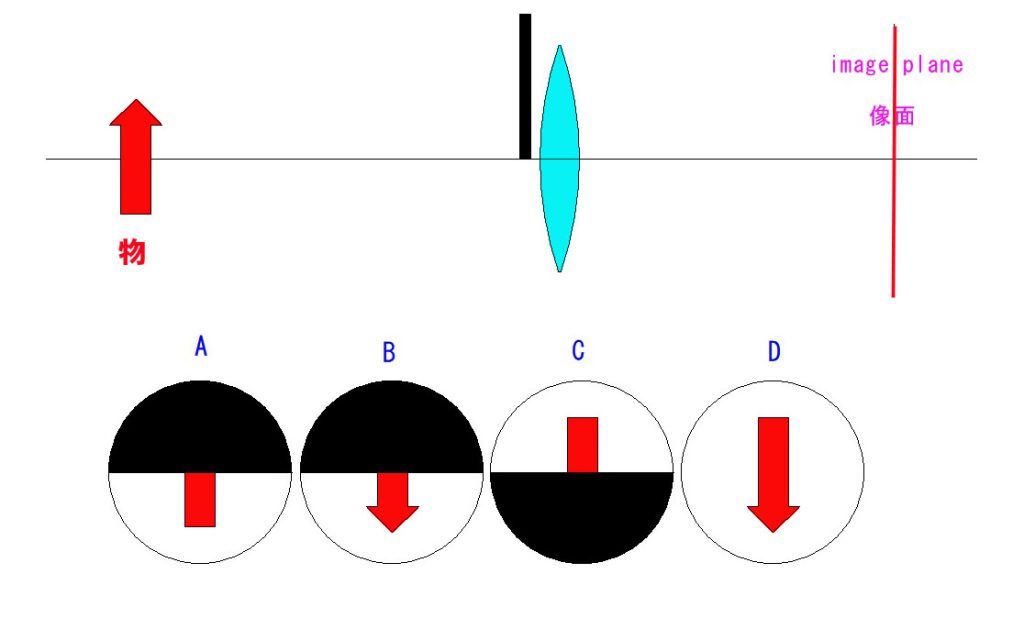
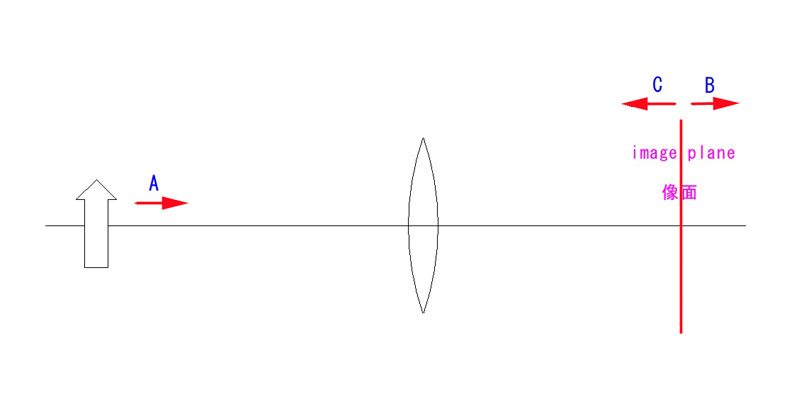
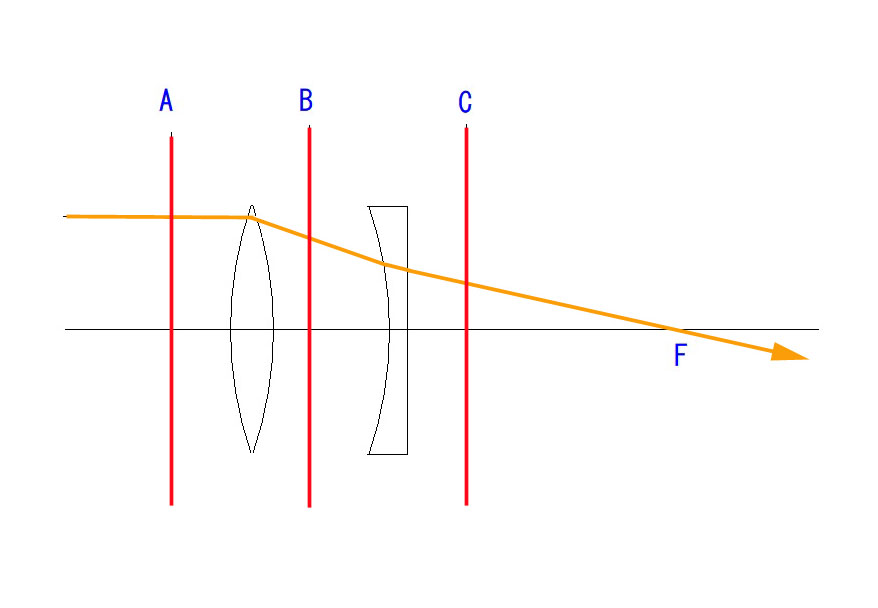
Q1以外は求値問題を避けた、概念的理解の問題です。

　当初、制限時間を5秒に設定しかけましたが、問題を読み取る時間もあるので、20秒に訂正しました。
　最後の問題（Q5）以外は、中学校、小学校レベルの問題だと考えています。
　時間内に答えられなかったり、少しでも頭を傾げた方は落第です。
　満点が取れなかった方は、大いに落胆、絶望し、猛省していただきたい。（私などは、ほぼ毎日絶望しています。^^;）
　落胆と絶望が反省と、真の理解のきっかけとなると信じるからです。
　私たちは文明の恩恵に浴して、日々生活しています。
しかし、文明の機器については、必ずしもメカニズムを理解していなくても使えます。
　スマホ・タブレットのゲームは、猫ですら興じます。
　今こそ、私たちは論理的に物事を考える姿勢が重要だと思うのです。
　視覚から直接入る、幾何光学的課題は、格好の教材だと信じます。

　くどいですが、屈折マトリックスは、２行２列の行列の右上の成分にその面パワー、その対角成分＝0，後の２成分は1で、行列式＝常に1です。

　移行マトリックスは、２行２列の行列の左下の成分に、面間隔×（-1）、その対角成分＝0，その他の成分は２つとも1で、これも行列式の値は1です。

　従って、その要素行列を何個つないでも、積算した最終行列の行列式も常に1なのです。

　なぜ、この事実に感動してくださる方がおられないのか、不思議でなりません。

　どうか、スルーすることなく、今回の問題にトライしてみてください。