ニュートンの公式も、過去に何度かご紹介しているはずですが、今回はより視覚に訴える Tutorial-Model をご用意しました。
　一般的な方程式 (1/s’ – 1/s = 1/f) を変形しただけなんですが、むしろ、ニュートンの公式の方が役に立つことが多いくらいです。
　一般の公式は、レンズ中心や主点が基点ですが、ニュートンの公式は、物側、像側の焦点が基点になります。基点になるということは、物点距離、像点距離をそこから測る、というわけです。符号の取り方は同じで、右向きを正、左向きを負とする鉄則は同じです。ｘ軸の正の方向を正とする鉄則、基礎光学の基本であり、叩き込んでおくことが重要です。
　基礎光学入門の最初のハードルかも分かりませんね。
　ニュートンの公式は、
　s s’ = – f² 　
　と、極めてシンプルな形であり、一般的な公式のように、一々逆数を扱う必要もありません。（標準公式と同じ文字 (s,s’) を使用しても、数値は異なりますので、ご注意ください。）
　まずは上の図から、
実物点と実像点が両焦点の外側にあるケースです。像点（物点）距離の取り方が、レンズ中心ではなく、両焦点であること、再度ご確認ください。
　まず、同じ色の結像ペアの距離同士を掛けてみてください。
値は、全て -f² となり、公式が成り立っていることに感激されるはずです。「なんで最初から教えてくれなかったの？」と言われそうですが、スルーして来られたのは、あなたの方です。^^;
　結像公式の練習の際も、これを知っておくと、非常に効率よく学習できます。　また、先日ご紹介した、光学系の非破壊検査にもこの公式が奏功します。
　下の図は、物点が虚物点の場合ですが、元の標準公式同様、虚像のケースにもそのまま適用できます。
　物点距離は、物側焦点から決めるのが鉄則、また、符号は右向きが正で、左向きが負になることも鉄則です。この辺の符号の扱いに慣れるのも、最初の関門でしょうね。
　先日、薄レンズの光路図の基本をご説明したばかりですが、それはそれで重要なポイントですので、無駄な努力にはなりません。

　ニュートンの公式を使えば、ブラックボックスのレンズシステムでも、非破壊で焦点距離は元より、主点位置まで何故分かるのか？ を可視化しました。説明不要と思います。

　余談になりますが、元来、スカラー量である、”距離”という概念を、一次元のベクトルに発展させる（方向性を持たせる）ことで、公式の応用性が飛躍的に向上しました。
　昔の、”1/a + 1/b = 1/f ” は、物点、像点距離 を純粋にスカラー（絶対値）として扱うため、凸レンズと凹レンズ、実像結像と虚像結像等、結像ケースごとに公式をいじる必要があり、非常に効率の悪いものでした。　しかし、最近、この古い手法がまだまだ現役で闊歩していることをネット上で知り、衝撃を受けました。
　距離に厳密な方向性（ｘ軸の正方向が＋）を持たせることで到達した、現在の一般的な公式 ★ 1/s’ – 1/s = 1/f (D) ★ は、あらゆる結像ケースに対応する、ユニバーサルな 近軸光線追跡 の強力なツールとなったのです。
　ほぼ同じ形に見えますが、飛躍的に応用性が高まった、最初の記念すべき革新だったはずです。
　距離を昔の”スカラー”でしが捉えられない方にとっては、高めのハードルかも分かりませんが、そこを克服すれば、最初の関門を通過したのも同じです。

　焦点や焦点距離よりも、ずっと難解なのが、像点や、物点の ”虚” の意味のはずなのに、今までに質問して来られた方は何故か皆無でした。
　この辺も、初学の方の躓きの原因かも？との思いから、先回りしてご説明します。
　まずは、上の図をご覧ください。物点 P が F (Lens-1 の像側焦点) を超えてレンズに接近すると、Q で屈折した光線 QR はＸ軸のマイナス方向に対して、図のように斜め上に射出するため、X軸のマイナス領域に実像を作ることが出来ず、X軸の＋領域の虚の点 P’から発散するように射出します。
　つまり、Lens-1 は、実物点 P の虚像点を P’ に結像させるということです。
　下の図は、上の図と同じ光線 RQ が逆方向から Lens-1 に投射された場合です。光の逆進の法則から、下の図の例も、上の図と全く同じ経路をたどるため、 物点と像点が交代しています。
　つまり、下図では、Lens-1 は虚物点 P の実像点を P’ に結像させているわけです。
　自然界には、収斂光束を発生させる物体は存在しませんが、Lens-1 の左に、Lens-2 のような別のレンズ系があれば、こうしたケースはごく普通にあります。下図は、まさしく、天体望遠鏡対物レンズとレデューサーの関係を再現しています。
　ただ、どちらも結像の主役は Lens-1 であり、光線RQ が 虚の物点 P に向けて投射されるなら、Lens-2 には意味がなく、何であってもかまいません。
　また、本例が示すように、物点と像点は常に立場を逆転させられるため、両点を共役点、両点を含んでｘ軸と垂直な平面を共役面、と言うわけです。物平面と像平面は、互換関係であり、共役面だということです。

　（今回は下図の例との比較のために、上図の光線の向き（左向き）が X 軸の負の方向（通常と逆）になっていますが、このままで結像公式を適用すると、Lens-1 のパワーの符号を反転させない限り、公式が破綻してしまいます。
　従って、通常は、光線の向きが x 軸の正方向と合うように、作図も最初から上図とは左右反転して描く( x 軸を反転する。）習慣にするのが無難です。　
つまり、レンズに入射する光線の向きがｘ軸の正方向になるように作図するということ。）

　満を持して投稿していた最近の光学講座が、相変わらず受け入れられなかった理由が、個別のご質問等から、ようやく分かって来ました。
　多くの（恐らくほとんどの）天文マニアの方が、超基礎の用語である、焦点、焦点距離、物点距離、像点距離等の言葉だけに慣れてしまい、長年の間に、その誤った解釈がバイアスとして根付いてしまっている、ということです。
　「焦点距離の意味すら理解していない！」と言うと、お怒りになるマニアの方もいると思いますが、それを仮定すれば、今まで、どんなに工夫してもご理解いただけなかった、あるいは面と向かって取り組んでくださらなかった理由の説明が付くのです。

　で、今日は、全く次元が異なる概念である、結像点（及び物点）と ”レンズの焦点” との違いを可視化してみようと思ったわけです。

　レンズの焦点 (F’ , F) というのは、レンズ中心 O と並んで、そのレンズ固有の動かない固定点であり、外部光線の影響で移動することはありませんし、レンズ自体を動かしても、レンズと一緒に移動するだけです。他のレンズと複合光学系を構成して、合成焦点を作ったとしても、元のレンズの焦点位置は、そのレンズのスペックとして、変化することはありません。

　物点を１→２→３→－∞ に移動させて行った時の像点が、最初は物点と同じ方向に移動していたのが、１’→２’→３’ を超えて行くにつれて急激に減速し、やがてそれ以上は左に移動しなくなる、極限の点（１’→２’→３’→ F ) を像側焦点と定義し、そのレンズのキャパを示す数値（焦点距離）とするわけです。
　レンズの度数と焦点距離は、その中心と共に、そのレンズのキャパを示すレンズ独自の指標であり、外部の物点を像点に移植する という、レンズの仕事結果とは全く次元が異なります。
　　図は、このレンズが、物点１～３を像点１’～３’に移植する仕事を表していて、近軸光学の主な目的も、各物点がどこに再結像するか？ということであり、F’,O,F の３点は、外部の 物点 を 像点 に移植するためのツールだとも言えます。

　ちょっと早いですが、解答をUPしますね。^^

　図の中に、A 例、B 例のレンズの結像方程式と、解答を示しました。
左上の角が座標系の原点で、上の右向きの横線が S 軸、左の下向きの縦線が D 軸です。S 軸の目盛り単位＝ｍ（メートル）で、Ｄ軸の目盛り単位＝ディオプトリー（ 1/ 焦点距離(m)）です。当然ですが、エクステンダーは凹レンズなので、度数には－が付きます。
　２つの曲線の交点に相当する点から、問題の条件を満たす、S と D が求まるわけです。
　問題の条件を満たす エクステンダー（A 例） に投射される虚物点（望遠鏡対物レンズの焦点）の 物点距離＝30mm 、エクステンダーの度数＝ – 16.666・・D、（焦点距離＝ – 60mm）ということになります。
　ややこしいですが、３ｘの拡大率が得られる物点距離 S とDの再現は、グラフではなく、座標軸を – s 方向に 0.01 移動することで得られます。
　このエクステンダーは、物点距離＝30mm で2倍、40mm まで繰り入れると、3倍のバローとして機能するということです。

　解説（＆解答）は、２～３回に分けて段階的に詰めて行きますので、途中で閃いた方は、すぐにお知らせいただけると幸いです。
　まず、超前提を誤解していては、全く先に進めません。
以前に、「鏡筒を３cm切ったら、対物レンズの焦点距離も３㎝短くなりますか？」というご質問があったことをご紹介しましたが、繰り出し装置を伸縮させても、対物レンズの焦点位置は微動だにしないこと！理解していましたか？　そうでなかった方は、上記の初心者さんの噴飯ものの質問を笑えませんよ！　ズボンの裾を3㎝切っても、あなたの脚は、3㎝短くなりませんから！　今回の問題で、まずはそこが一番重要な前提です。　前回、”レンズ系の非破壊検査”の方法について、ご紹介しましたが、今回の問題に数式すら組めなかった方は、非破壊検査の記事も曖昧なままスルーしておられた方です。
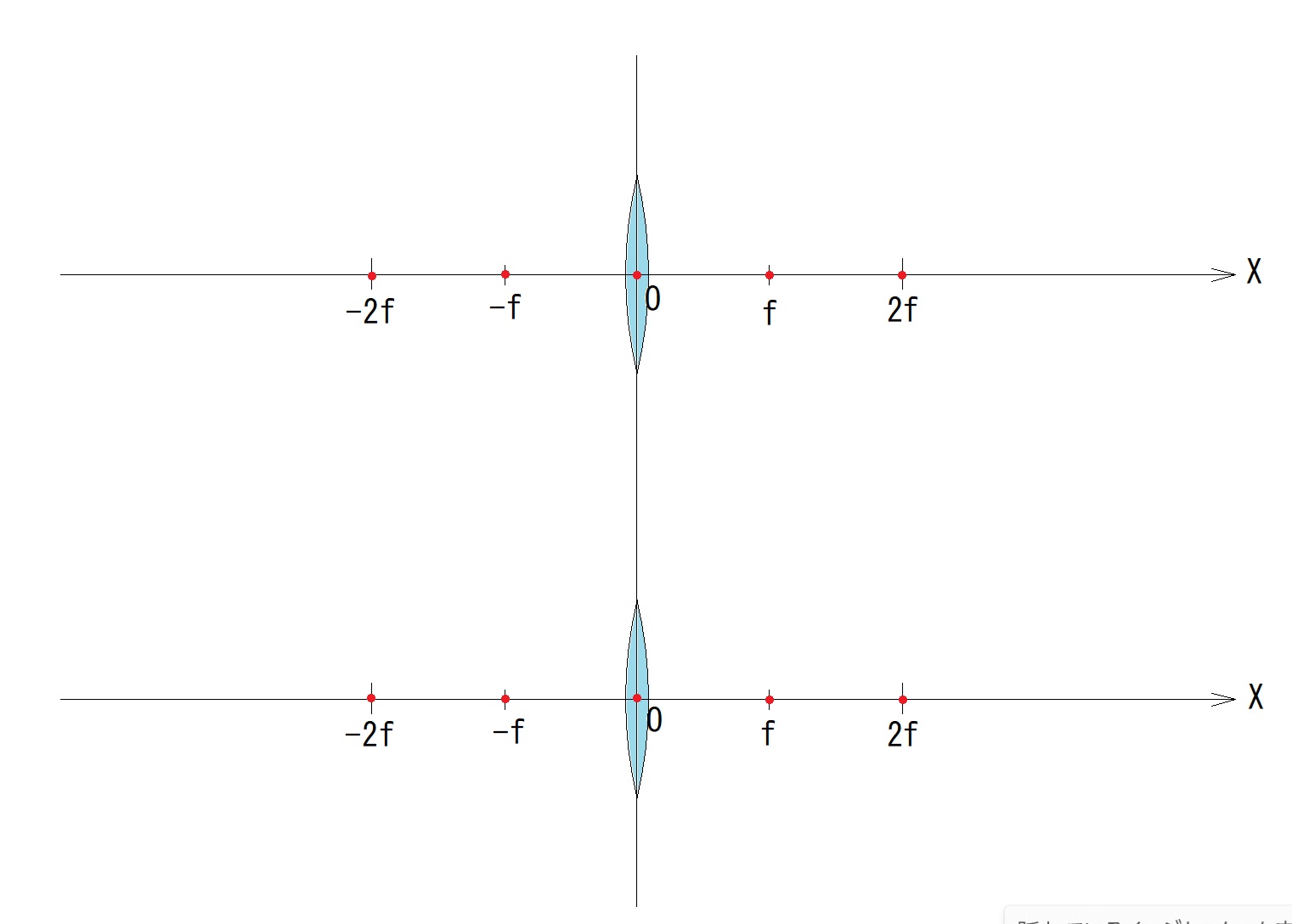
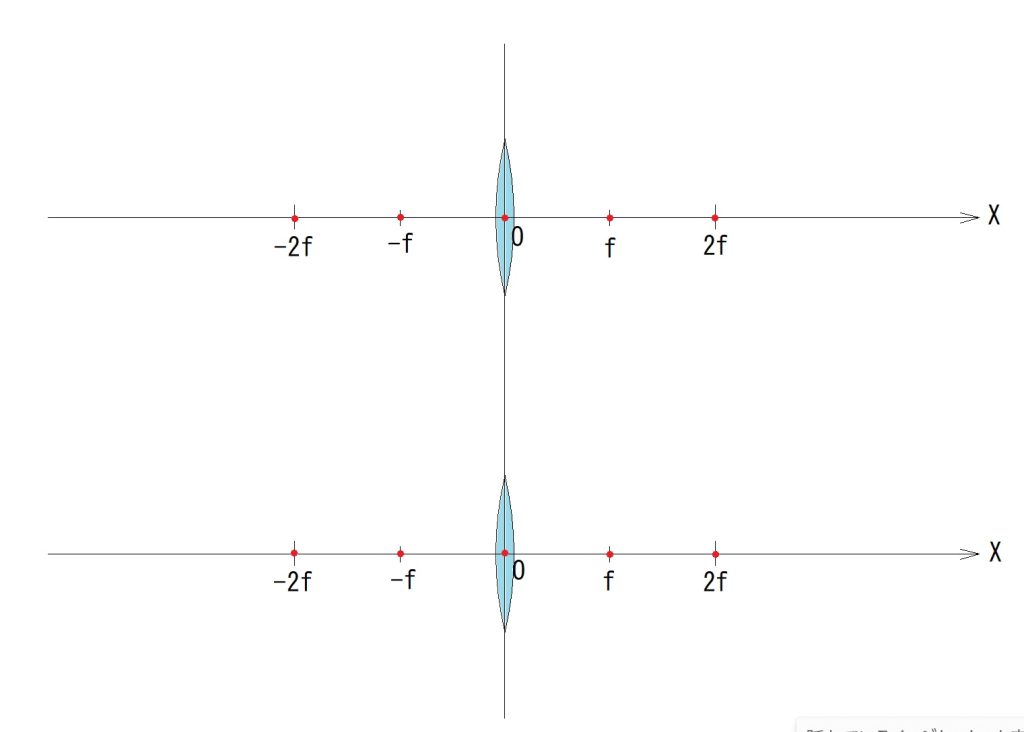
　対物レンズの焦点位置は動かないこと、まずは、それがこの問題の最初にして重要な前提です。望遠鏡のスペックが分からない、というのも、望遠鏡のスペックはこの問題に全く関与しないということです。
　この問題の主役は、”エクステンダーユニット”であり、他は全て脇役なのです。
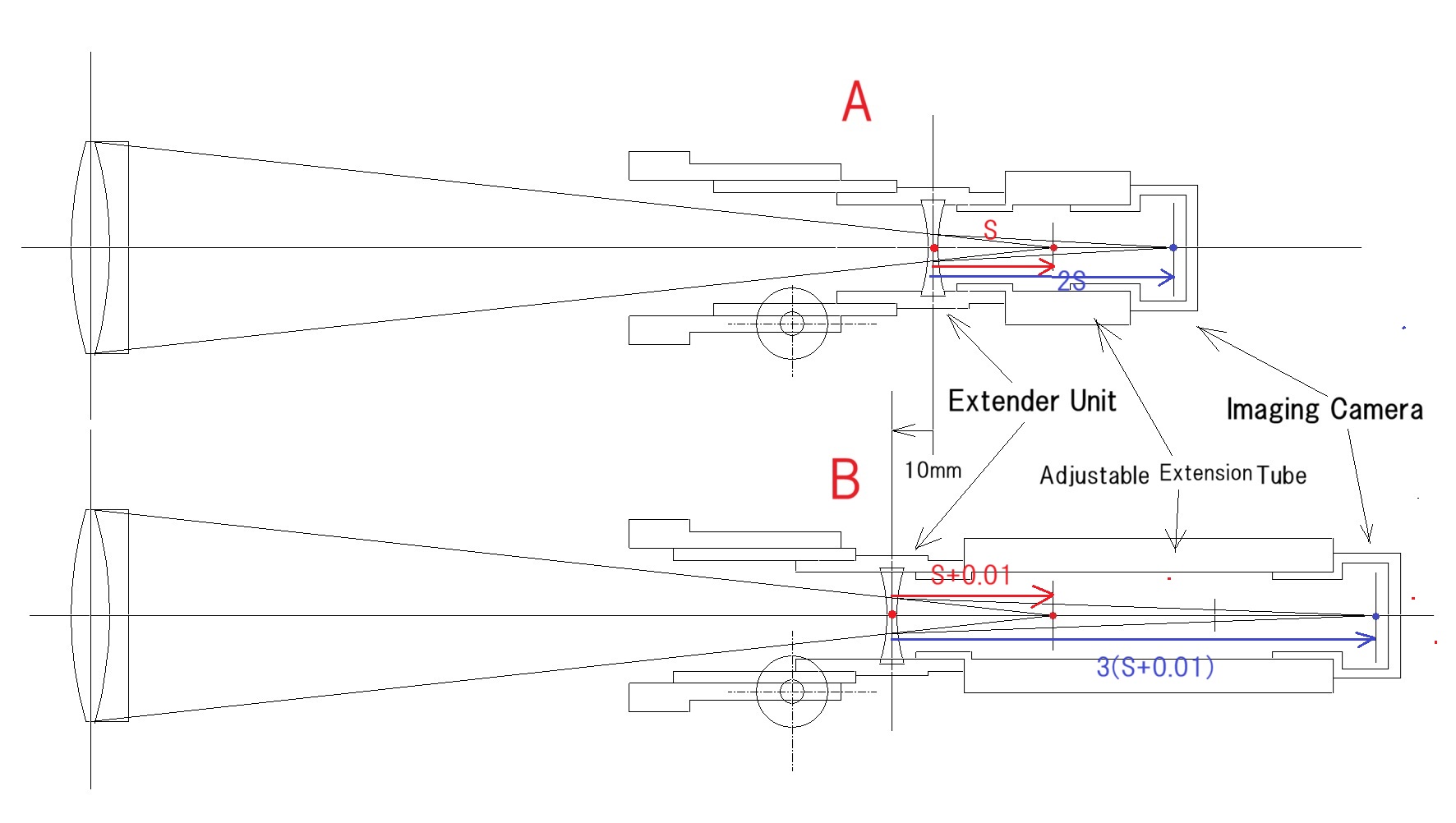
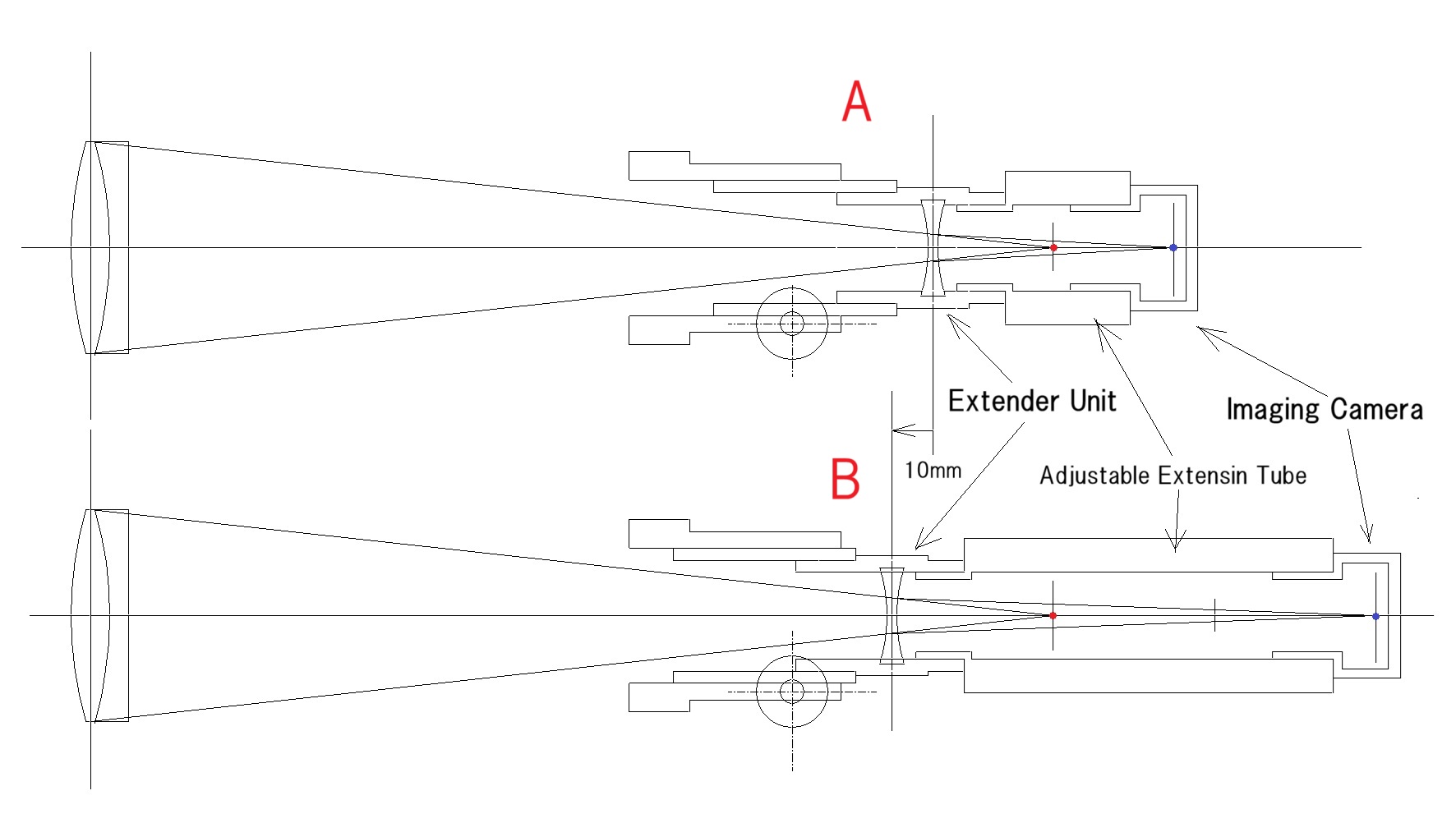
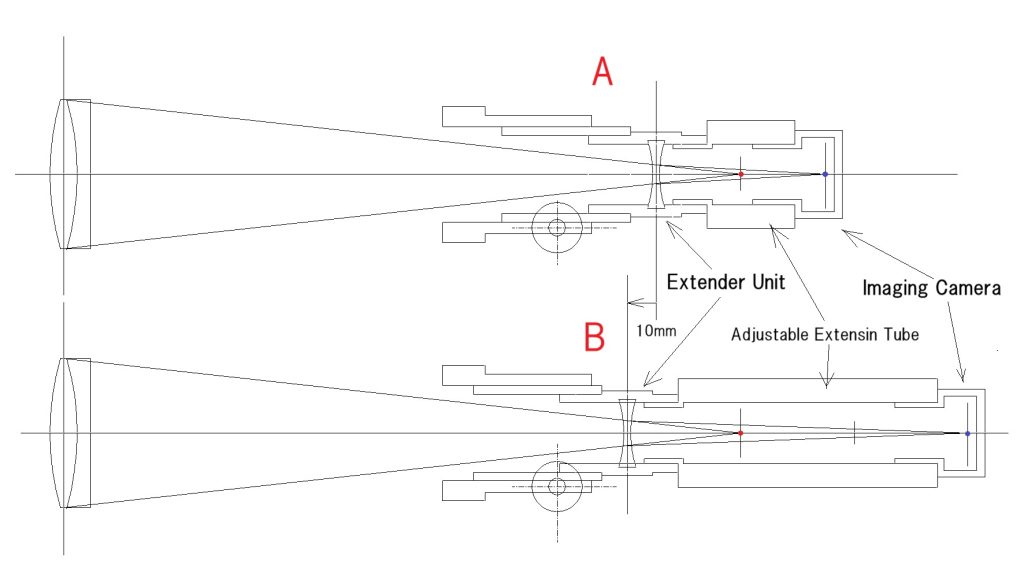
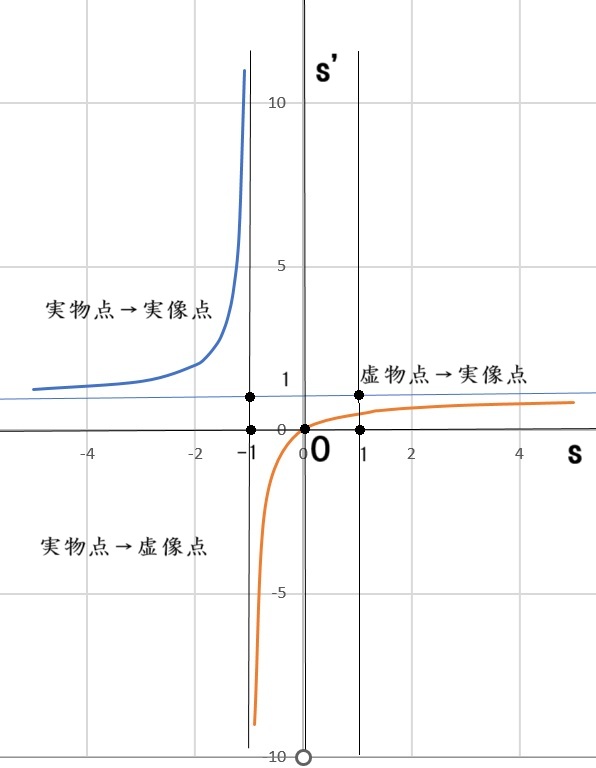
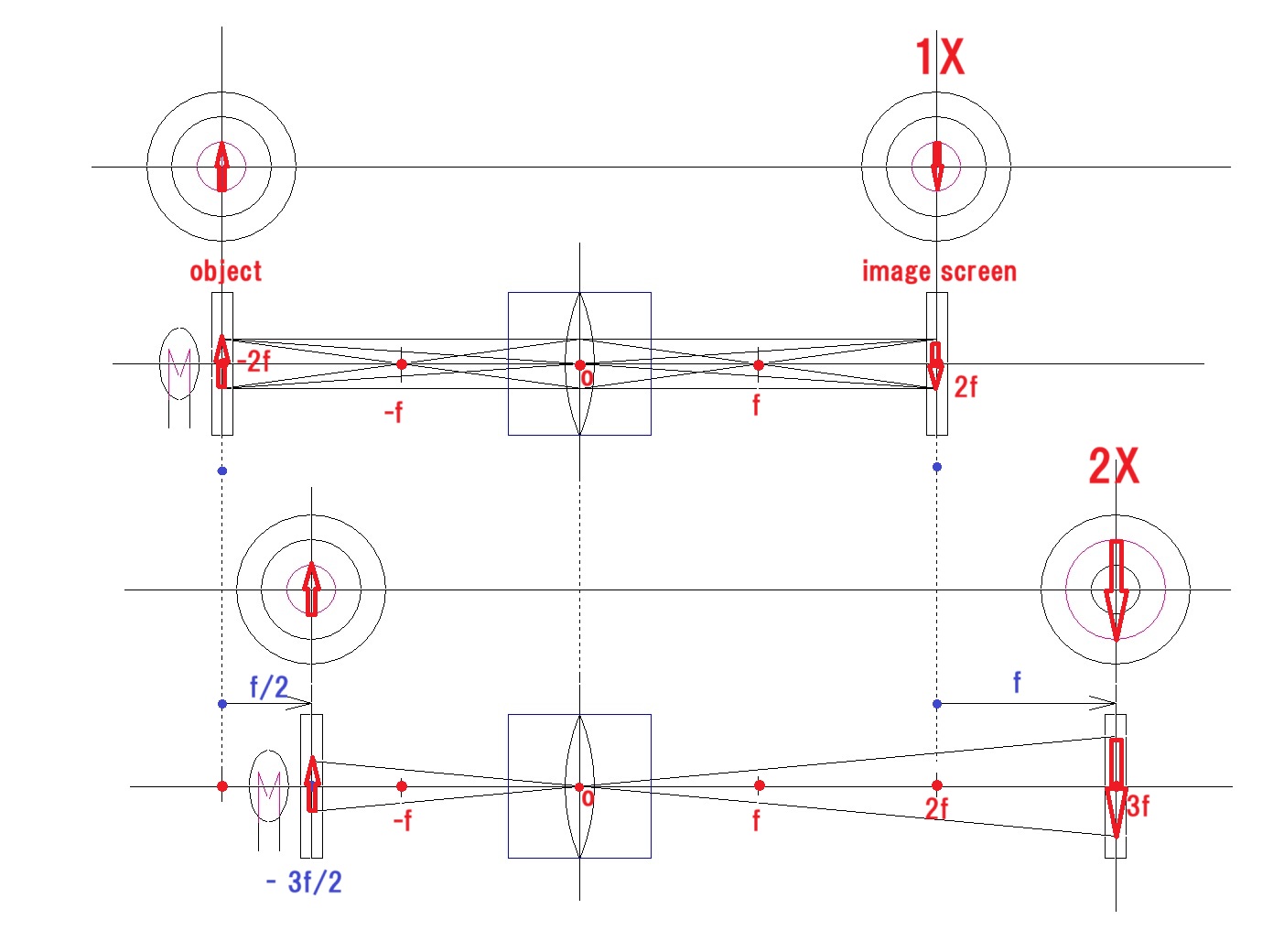
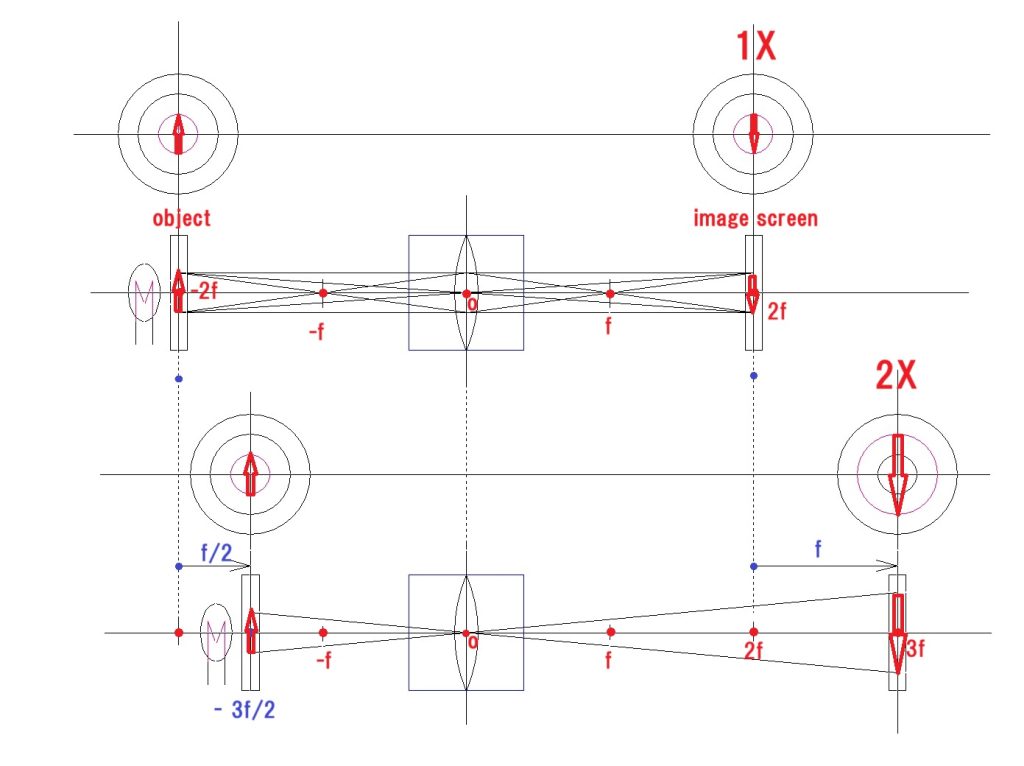
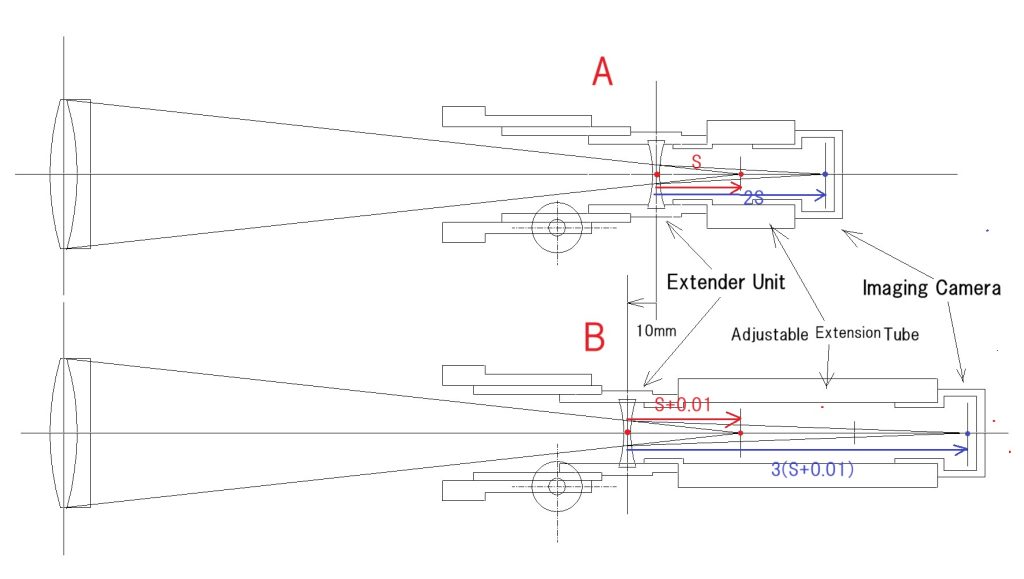
　エクステンダーの虚物点であり、動かない点である、対物レンズの焦点に対して、2倍の拡大率を確認したエクステンダーを10mmだけ対物側に移動させたら、拡大率が３倍になりましたよ！　という問題です。
　1/s’ – 1/s = D (1/f) に未知数を代入し、A 例と B 例で２つの方程式が組めれば、この問題は解けたも同じです。
　ここで、問題になるのは、A 例 だけでも、公式の形のまま、未知数をS, S’ ,D としてしまうと、方程式が２つあっても、未知数が３つになるので、計算に難航し、挫折してしまうでしょう。
　問題の条件に、拡大率＝2倍、３倍、とあるので、A 例では、S’ = 2S なので、そのまま代入します。3つの未知数が２つに減り、問題解決の道が開けます。
　B 例は、S,S’ とも、A 例とは、異なります。それを T,T’ とすると、1/T’ – 1/T = D (1/f) となりますが、A 例と同じ未知数を使用しないと、問題は解けません。問題の条件から、T=S+0.01, で、T’ = 3T =3(S+0.01) として結像公式に代入すれば、A 例と同じ未知数 を使用した、もう一つの方程式が組める訳です。
　２つの方程式さえ組めれば、以下の連立一次方程式と大差ない問題になります。
x + y = 5
2x + y= 6

「基礎光学の知識が何の役に立つのか？さっぱり分からん！」とか、友人から言われ続け、初心者の方に分かりやすい説明を模索して来ましたが、レベルを単に下げるよりも、多少難しくても、”役に立つ！”ということを分かってもらえる練習問題も良いかな？と、この問題を作りました。

問題の条件；
　上図のように、エクステンダーレンズユニットを繰り出し装置に固定、それに何らかのアジャスタブルな伸縮管を介して、撮像カメラをセットします。
　エクステンダーユニットは、焦点距離、パワー、主点位置、レンズ構成枚数 のどれも分からないブラックボックスとします。
　分かっているのは、
1. 短めの延長管で、丁度望遠鏡の直焦点に対して、2.0 倍の倍率が得られたこと。(A)
2. その状態から、きっちり10mm 、繰り出し装置を繰り入れたところ、延長管の延長により、ピントが合った時点の倍率＝3.0 倍となることが分かった。(B)
・・・の上記２点のみ。
　望遠鏡のスペックも隠されていて、延長管の長さや延長量も分からないものとします。分かるのは、エクステンダーレンズユニットを10mm繰り入れたことと、２例の倍率だけ。

問題；　このエクステンダーユニットのパワーと焦点距離を、上記２点の条件のみを使って求めよ。（小数点以下、3桁で切り捨て）
（結像公式：1/s’ – 1/s = D (1/f) が活用できるかどうかの問題。式を丸暗記しているだけではダメで、理解し、応用できないと役に立ちません。）
　図の赤いドットは対物レンズの主焦点で、繰り出し装置を動かしても動きません。濃紺のドットがエクステンダーとの合成焦点で、エクステンダーと対物主焦点との位置関係で大きく移動します。

　焦点距離 f ＝１ｍ(1D)の対物レンズの物点距離(s) と像点距離(s’)の関係式、1/s’ – 1/s = 1 (1/f) を可視化してみました。
　元来は、s と s’ は、レンズ中心が原点の x 軸上の数値 のため、s を x 軸に、s’ を y 軸に設定したので、不慣れな方は返って混乱されるかもわかりませんね。
　物点がレンズの左側にあって、光線は左から右に進む前提です。　第２象限の青い曲線が、”実物点 → 実像点のグラフです。（レンズを挟んで、左に物点、右に像点の典型的な実像結像の曲線です。）
　レンズから ±１ｍ 以内の実物点は実像を結ばないこと、先日ご提供した薄レンズの結像図のテンプレートを練習いただいた方は、感覚的に体感されたはずですが、数学的に検証すると、こうなります。s = -1 と s’ = 1 が漸近線になりますね。

　天体望遠鏡は、鏡筒があるので、接眼側からあまり深くレンズに接近できませんが、対物レンズ単体で考えると、逆方向からの結像もあるので、逆追跡の結像グラフもお示ししました。
　どちらにしても、第２象限の s ＜ -1m , s’ ＞ 1m と、第１象限の s ＞ 1m , s’ ＞ 1m が 実物点が実像点を結べる範囲で、両サイドからの結像を考えても、レンズの前後の両サイド、≦ 焦点距離　には、実物点と実像点は共存できないことが分かります。s = ± 1 と、s’ = 1 が漸近線になりますね。

、実物点と実像点が

　光路図練習用のテンプレート、ほぼ反応がなかったので、使用例をお示しします。
　確認のためにもう1本の光線を加えても結構ですが、像点を決定するのには、２本で十分です。
　また、像モデルは矢印で良く、わざわざ蝋燭の絵を描く必要はありません。
　実際に作図してみることで、実像が出来ない範囲等、体感できると思ったんですがね。