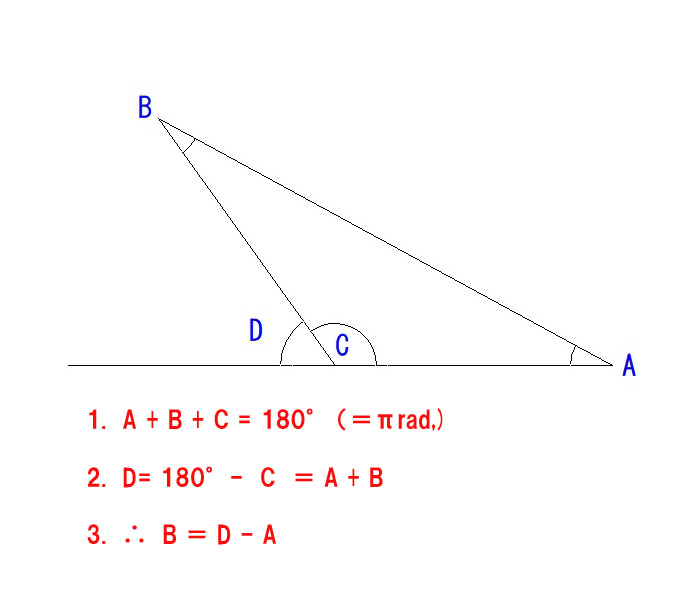
4.　三角形の基本定理です。∠A + ∠B + ∠C＝180° (πrad.)
5. 　∠Cの補角、∠D＝∠A + ∠B
6. 　上記より、∠B＝∠Dー∠A

　以上、三角形の基本中の基本の定理ですが、よく使うため、改めてご説明しました。
ここまで、準備運動1,2の項目について、連番を１～6まで振りましたので、分からない方は、何番から分からないのかをお知らせいただければ、さらにご説明します。　

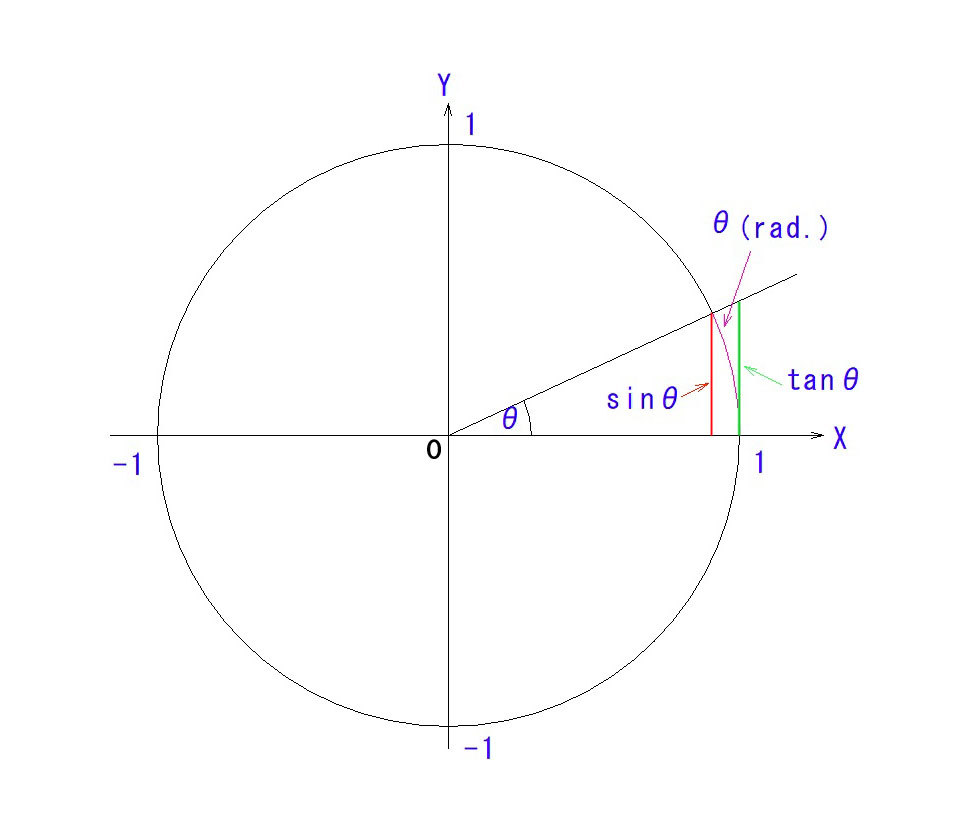
1.　後先になりましたが、準備運動からやりましょう。
　幾何光学で扱う角度は、断りが無い限り、一周360°の角度（度数法）でなく、ラジアンという単位（弧度法）の角度です。弧の長さが半径の何倍か？ということです。図の単位円（半径＝1の円）の、θの弧の長さのことです。

2. そして、sinθは、図の赤い直線の長さ、tanθは緑の直線の長さです。

3.　θ → 0　のとき、sinθ も tanθ も θ に収束するので、全てθとして扱っても差し支えないのです。
　　試しに、度数法の３°について、三者の数値がどうなるか、計算してみましょう。
　　sin3°＝0.52335……..
　　3°　＝0.52359… rad.
tan3°＝0.52407…..

3°付近でも、すでに3者の数値はかなり収束しています。角度がゼロに近付く（ほぼ光軸上）ほど、3者が収束することにご納得いただけたと思います。また、上図からも、グリーン、マゼンタ、レッドの3つの直線／弧 の長さが、θ→0のときに収束して行くことは、直感的にもご理解いただけるはずです。

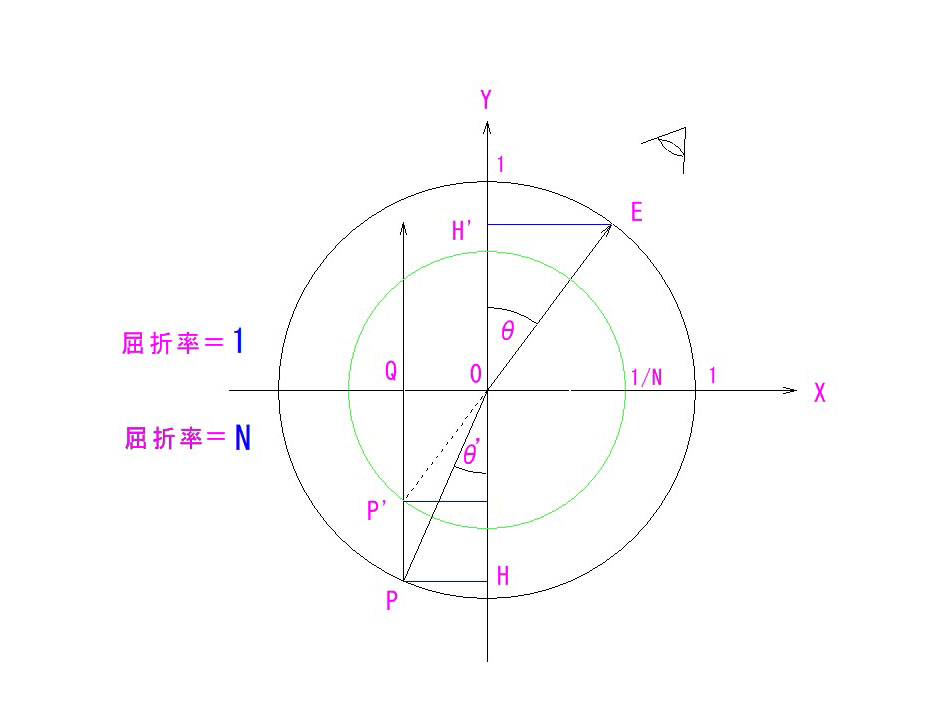
　今回は、理解できる、できない、の問題ではなく、すでに立証されている屈折の法則をご説明するものなので、素直に受け入れて、覚えていただく必要があります。

　屈折率がNとN’の界面に於いて、入射光線の入射角＝θ、屈折角＝θ’とすると、
Nsinθ＝N’sinθ’　となることはすでにご存じと思いますが、それを可視化すると、上図のようになります。よりシンプルにするために、N＝1（空気中）としています。
EH’/PH＝N　が屈折の法則、そのものになります。（OP/OP’=N と考えても同じ）

　Y座標の負領域が屈折率Nのガラスあるいは液体と考えてください。
Eから見ると、点ＰがＰ’に浮き上がって見えるわけです。
その浮き上がりは、OP/OP’=Nなので、厳密には QP/QP’ ≠ N なのですが、θ → 0 のときに、QP’ → OP’、QP → OP に収束するので、近軸領域では、QP/QP’ ＝ N　として差し支えないのです。

　ここでお分かりのように、反射の場合は、反射面が平面であれば常に完璧な結像を結ぶのに対し、屈折の場合は、たとえ界面が平面でパワーがゼロであっても、諸収差を免れないということです。
　従って、θ → 0 で、sinθ＝tanθ=θ (単位はrad.)の近似が成り立つ近軸領域に限定した、シンプルな公式 (Nθ＝N’θ’) を立てるわけです。この辺の近似の考え方が、多分、初学者を混乱、落胆させる要因だろうと思います。
　近軸公式だから、現実では役に立たないのではなく、無収差の理想光学系であれば、近軸の結像状態が全体を代表するし、そうでない場合は、光軸から離れた光線も同じ結像をするように設計努力するための目標、指針、骨格を提供するわけだから、近軸公式の存在意義は十分に大きいものがあるのです。

　4回までの講座について、理解いただいた方がほぼ皆無なのは何故だろう？
どうやら、基礎の基礎、物（ぶつ）と像（ぞう）の意味が分かっておられないのでは？と思う。
　もしかしたら、これが突破口になるような気がする。
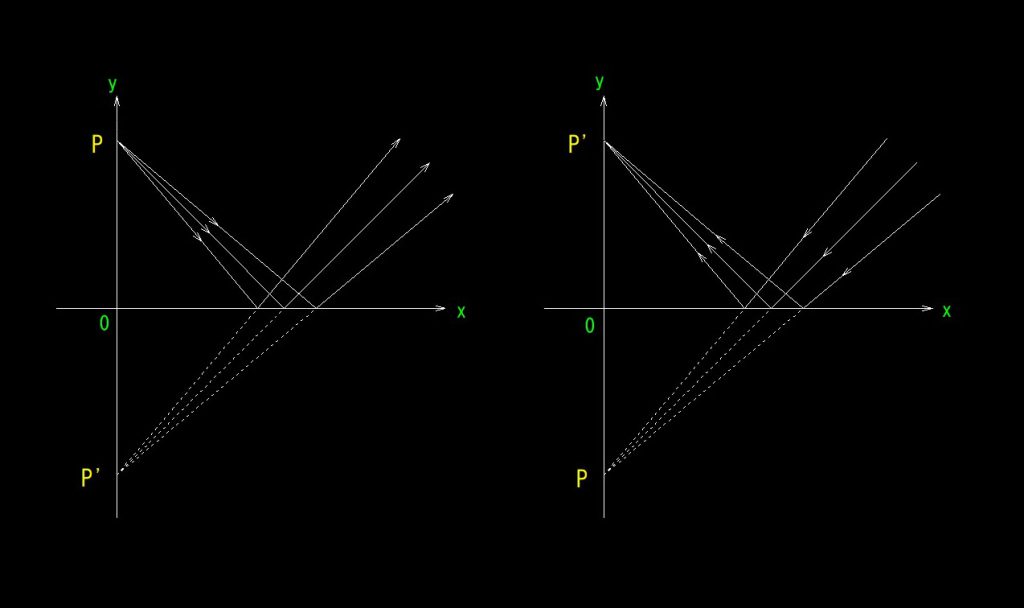
　一番シンプルな光学系である、平面鏡をモデルにする。
　XZ平面が鏡面とする。左の図を見てください。
実物点Pから発した光線は全てXZ平面に対して対称な点であるP’から出射したようにXZ平面で反射する。作図していない、どの光線も同様に振舞う。一般に、光路図では、せいぜい1本か2本の光線しか描かないので、誤解している方が多いと思う。図は便宜上Ｙ軸の正領域の一点に物点を置いたが、XZ平面より上の物空間にあるどの点も、Ｙ座標の符合が反転するだけで、X,Z座標の値は変化しない。

　次に、右の図を見ていただきたい。
物と像は逆にもなる、つまり共役だということを示しています。
自然界では滅多にないが、Ｐに向かって収斂する光束は全てP’に実像を結ぶ。
Pを虚物点と言う。虚像点P’も、虚物点Pも手で触ることは出来ないが、それぞれが立派な点である。

　実体は同じでも、表現（表示）方法によって、計算の難易が桁外れになることが多いわけです。
物点、像点距離を用いるよりも、光線の基点の高さと傾き、またレンズは焦点距離ではなく、度数で表現した方が、計算がずっと楽になる例を、過去2回に分けてご説明したのですが、より端的な例をご紹介します。
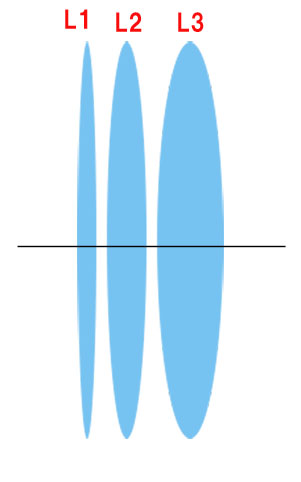
　上図のように、L1,L2,L3の3枚の薄レンズを密着させた時（つまり間隔は.0とする）の合成焦点距離を考えます。焦点距離は、L1から順に、2000mm,1000mm,400mmとします。
この3枚の合成レンズ系の焦点距離は何ミリになるでしょう？
　手慣れた方は、暗算で即答されるでしょうが、そうでない方は、案外手こずるのではないでしょうか？　1/S’ -1/S = 1/f　を律儀にレンズごとに計算して行ったら、大変面倒です。
　L1～L3 を度数(1/f)で表したらどうでしょう？
　L1 から順に、+0.5D, +1.0D ,+2.5D ということになり、合成パワーは単純に足し算をすればよく、0.5+1.0+2.5=4.0(D)　となります。合成焦点距離(m)は、その逆数だから、f =0.25ｍ (250mm)
となる訳です。

　

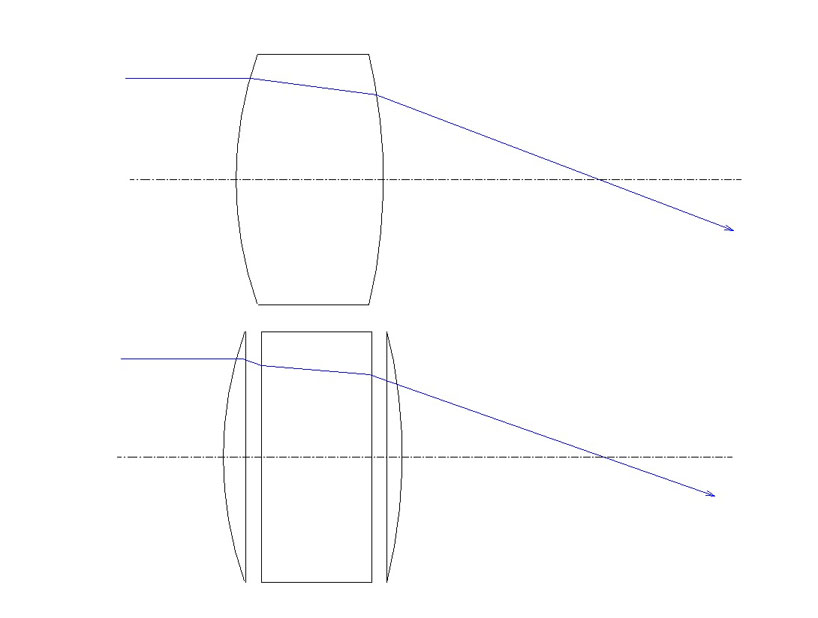
　前回の近軸追跡に於ける行列の応用は、空気中の薄レンズ（厚みを無視できる）に限らず、一般的な光学系に応用できます。
上図（敢えて解説を省いた）から直感的にご理解いただけると思いますが、厚いレンズも、両端の薄い平凸（もしくは平凹）レンズの間を、屈折率Nの平行平板で満たしたものと考えられます。
　そして、傾角成分αについて、新たにNα＝α、厚みＴ＝T/N を定義すれば、空気中の薄レンズのシステムと全く等価なものとして扱うことが出来るのです。（厚さＴの平行平板（屈折率Ｎ）は、T/Nの空間と等価）
屈折率Ｎ中の傾角はN倍、移行距離は1/N倍しておけば良いということです。

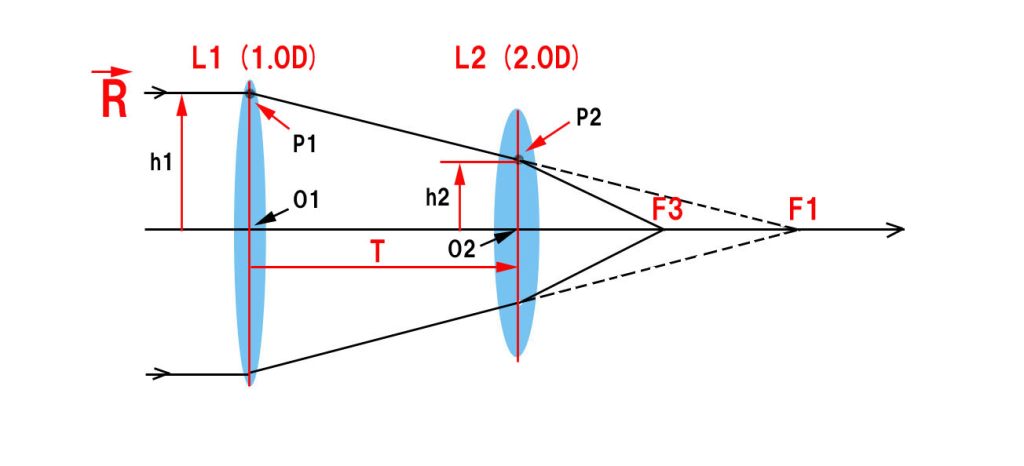
　出来るだけハードルを低くするため、薄肉の2枚レンズ系（度数も配置も具体的に指定）でご説明します。入射光線から順に、レンズL1のパワー（度数；1/焦点距離m）＝1.0D、L2=2.0D,　レンズ間隔Ｔ＝0.5mとします。（f1=1000mm, f2=500mm）

　近軸結像の公式として 1/s’ – 1/s = 1/f —–式１ があり、それをレンズごとに駆使すれば、合成焦点の位置から、合成焦点距離、主点の位置等まで求められますが、レンズ枚数が増えるほど、計算が煩雑になって行きます。レンズを通過するごとに、レンズ間隔を調整したり、s’ の逆数を求めたりしないといけません。
　式1は、物点距離＝s　、像点距離＝s’、焦点距離＝f と置いていますが、ここで、1式の両辺に、”h”を掛けてみます。hは光線の指定位置に於ける光軸からの高さを表します。
すると、1式は、
h/s’ – h/s =h/f　　　となります。
　さらに、1/f =Φ（レンズのパワー）、また、h/s’ 、h/s　を、光線の傾き(tangent)として定義し、
h/s’＝α’、h/s＝α とすると、
α’＝α＋hΦ　と書けます。
（近軸式なのに、hを定義するのはおかしいのでは？と思うかも知れませんが、もともと、ｈは元の式の両辺に平等に掛けた数値であるため、単位はもとより、いくら大きな数値を設定してもかまわないのです。）

　αは、屈折する点に入射する直前の光線の傾き、α’は屈折後の光線の傾き、h は入射点の光軸からの高さを表します。傾斜角の正負は、光線同様に（レンズに対して）右側の結像点（物点）距離が＋になるように設定します。（右下がりの傾斜が＋）
　屈折直後の h’ は h と変わらないので、
h=h’　となります。
以上から、屈折マトリックス（行列）として、以下の行列が定義されます。（Φはレンズのパワー）

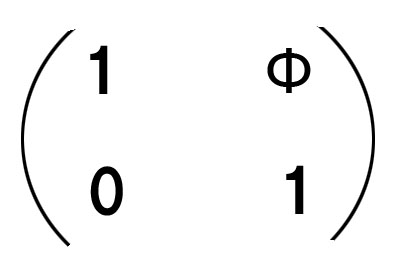
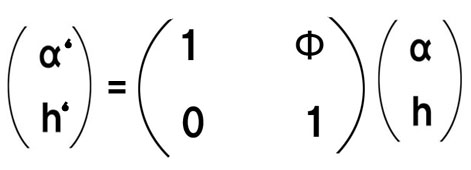
上記を行列表記でまとめると、こうなります。↑

レンズL1とＬ2の間は屈折が起こらず、hだけが変化するので、
α’＝α、h’=h-αt となります。
行列で表記すると、

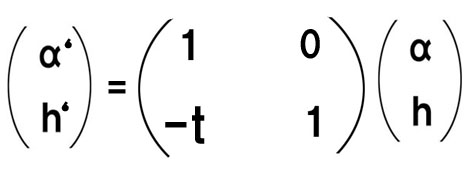
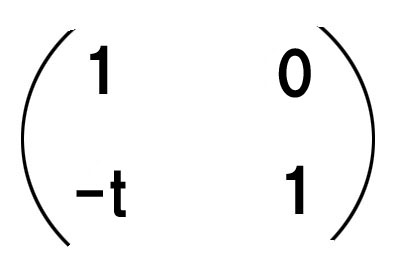
　　　　　　　　　　　　を、移行マトリックスと言います。
　両マトリックスとも、行列式の値は”1”であり、いくら掛け合わせても、結果の行列の行列式も常に1であることは、注目に値します。それを利用すると、一見絶望的に複雑な主点位置の計算も、いとも簡単に解けるわけです。

　お察しのように、レンズが何枚になろうと、屈折と移行のマトリックスを順に掛け合わして行けば、焦点位置、距離、途中の光束の太さから主点位置まで、簡単に求めることが出来るわけです。
　では、実例に則してやってみましょう。
2枚のレンズのパワー(1/f）は順に1.0Dと2.0D、間隔＝0.5mとします。
（Dはレンズの度数単位で、焦点距離（m)の逆数。）

　行列の計算順序の都合により、上の光路図のレンズの並びと該当行列の並びが逆になっていることにご注意ください。
（　　）は、右端から左向きに、L1の屈折マトリックス→Ｔの移行マトリックス→L2の屈折マトリックスとなります。この掛け算を行うと。

となり、これを、L1～L2までのシステムｰマトリックスと言います。
(行列の掛け算は、結合法則は成り立ちますが (AB)C=A(BC)、交換法則は成り立たない ABC ≠CAB のでご注意ください。）
　このシステムマトリックスに、左から、高さ(h)＝1で、傾角＝0（光軸に平行）の光線を投入してみましょう。行列式は、

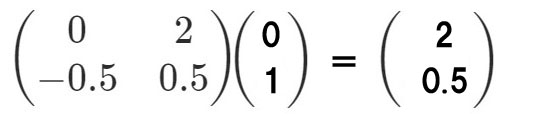
　これは、ｈ1＝1の高さでL1に入射した光線が、L2上の点P2で屈折した直後の光線の要素（傾角と高さ）を表しています。これから、この2枚レンズの合成パワー＝2.0Dであること、また、h2＝h1/2であることも分かります。
　また、この例に限らず、システムマトリックスの右上の成分が常にシステムのパワー（度数）になっていることにもご注目ください。

では、今度は、L1のパワーをA、L2のパワーをB、Ｔ＝レンズ間隔 として、L1～L2のシステムマトリックスの一般式を導いてみましょう。

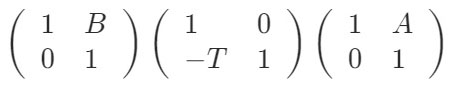
計算すると、

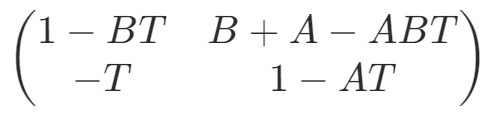
右上の成分がこの2枚レンズ系の合成パワーですが、何か、見覚えはありませんか？
（D=D1+D2 – D1XD2t　は2枚レンズの合成パワーの公式）

—-つづく